Table of Contents
You are familiar with geometric shapes such as point, line, angle, triangle, quadrilateral, circle and plane. In this article we will revise what you have learnt.
Geometric Shapes – Point
A point is a basic geometrical shape/ object. It has some position but neither nay length nor any breadth.
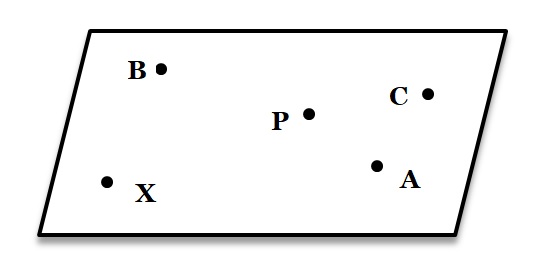
To represent a point on paper, we make a dot using a sharp pencil. We denote points by capital letters, such as A, B, C, P and X.
Collinear Points
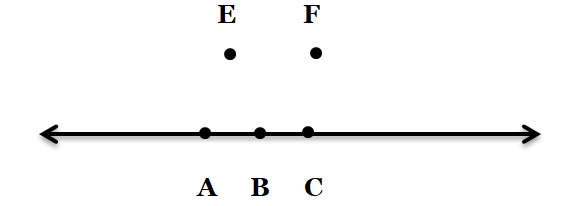
If three or more points lie on a straight line, we say that these points are collinear. In the figure, A, B and C are collinear points, while A, E and F are non-collinear points
To learn more about the point in geometry you can read the post : Definition of Point in Geometry and 3 Types of Points
Geometric Shapes – Line
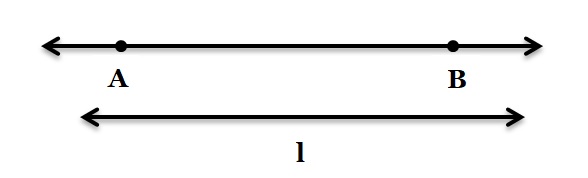
A straight line (simply called a line) is formed by a collection of points. A line has some position, shape and length but neither any breadth nor any thickness.
It can be extended on either side to any length; so it has no end points. In figure, this is shown by arrowheads at either end of the line. A line is denoted by any two points on it; for example, line AB. It may also be denoted by a small letter (e.g. l, m, n, etc.).
Ray
A ray is a part of a straight line. It extends indefinitely in one direction from a fixed point. In figure, this is represented by an arrowhead in one direction.
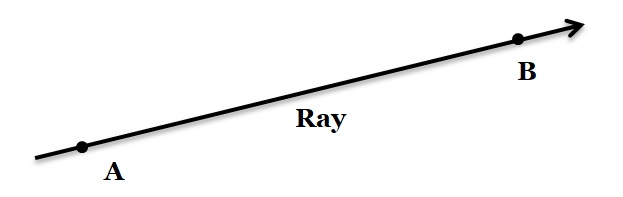
A ray has one end point – the fixed point from which it starts is called the initial point. It is denoted by the initial point and any other point on it, such as ray AB.
Line Segment
The part of straight line between two given points is called a line segment. A line segment has two end points and finite length. The line segment between the points A and B is denoted as \[\overline{AB}\]

If C is a point on the line segment AB such that AC = CB = ½ AB then C is called the middle point (or midpoint) of AB.
Properties of lines
The following properties of lines are to be universally true.
- Property 1: There are an infinite number of points on a straight line.
- Property 2: An infinite number of straight lines can be drawn through a given point.
- Property 3: One and only one straight line passes through two different given points (or two distinct points determine a straight line).
- Property 4: Two different straight lines cannot have more than one point in common.
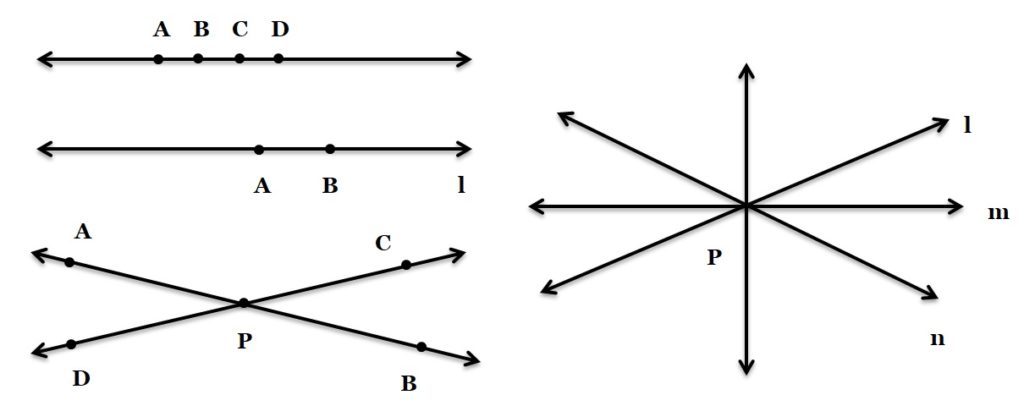
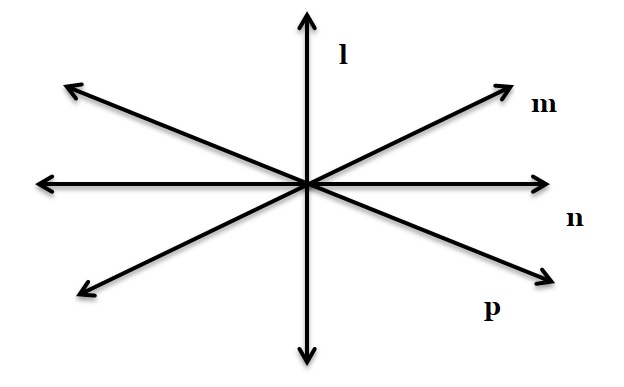
Concurrent Lines
If three or more straight lines have one point in common then these lines are called concurrent lines. In the figure, l, m and n are three concurrent lines and O is the point of concurrency.
To learn more about the lines in geometry you can read the post : 5 Types of Lines With Properties & Differences
Geometric Shapes – Triangle
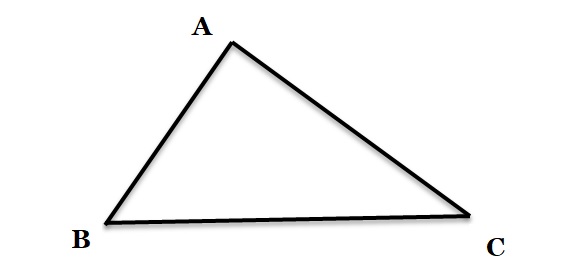
A triangle is a plane that is bounded by three straight lines. In the figure ABC is a triangle.
A triangle has a total of three parts. Three sidess, three angles and three vertices.
Geometric Shapes – Quadrilateral
A plane bounded by four straight lines is called a quadrilateral. In the figure ABCD is a quadrilateral.
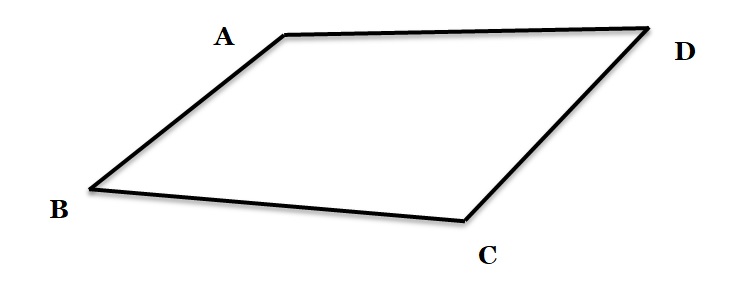
Every quadrilateral has four sides, four angles and two diagonals.
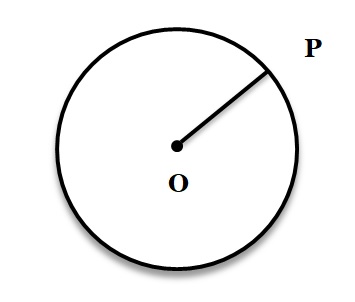
Geometric Shapes – Circle
A circle is a shape consisting of all points in a plane that is a given distance from a given point, the center; equivalently it is the curve traced out by a point that moves in a plane so that its distance from a given point is constant. The distance between any point of the circle and the center is called the radius.
Geometric Shapes – Plane
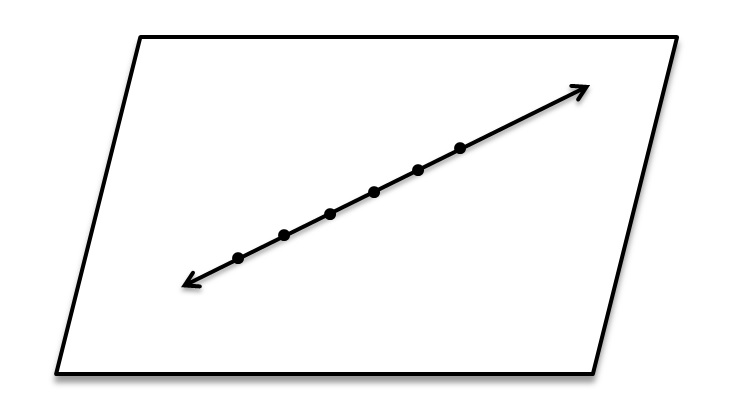
A plane is a flat surface that has some length and breadth but no thickness. The surface of a sheet of paper and a tabletop are examples of a plane. In fact, they are parts of planes, because a plane is supposed to extend infinitely. It is made up of an infinite number of lines and hence and infinite number of points.
An important property of a plane
If two points on a line lie in a plane then every point on the line lies in the plane. This follows from the fact that two point are enough to determine a straight line.
To learn more about the plane in geometry you can read the post : Surface in Geometry and Its 2 Types
| Quiz |
[WpProQuiz 2]
Solid Body |
5 Types of Lines |


