Table of Contents
Rectangular Cartesian Coordinates
In solid analytical geometry, the position of a point is determined by the coordinates with reference to three axes in space.
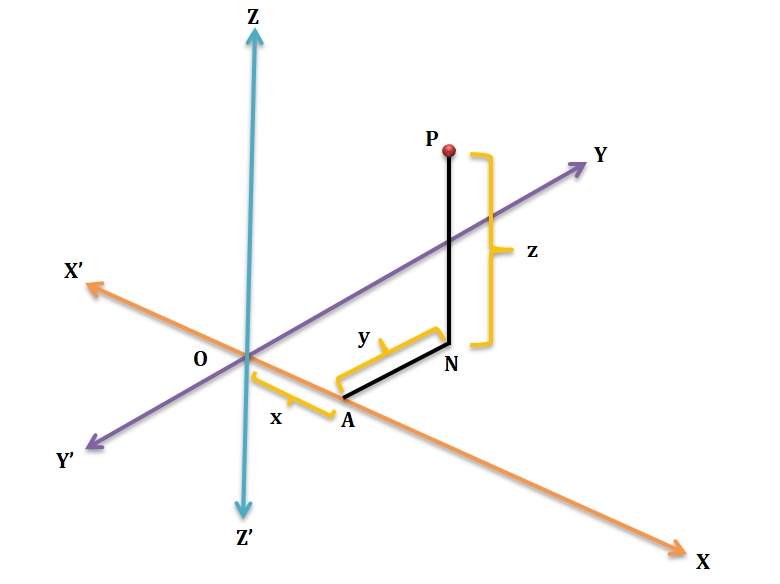
Let us take three mutually perpendicular straight lines X’OX, Y’OY and Z’OZ meeting at O. Let P be a point in space. Draw PN perpendicular to the plane XOY and NA perpendicular to OX. Let OA = x, AN = y and NP = z. The position of the point P is determined by these three distances called the coordinates (x, y, z) with reference to the three axes OX, OY, OZ, called the x-axis, y-axis and z-axis respectively. The coordinates of the origin O are (0, 0, 0).
The planes YOZ, ZOX, XOY are called the co-ordinate planes. Through P draw planes parallel to the coordinates planes. These planes combined with the three co-ordinate planes form a parallelepiped having six rectangular faces.
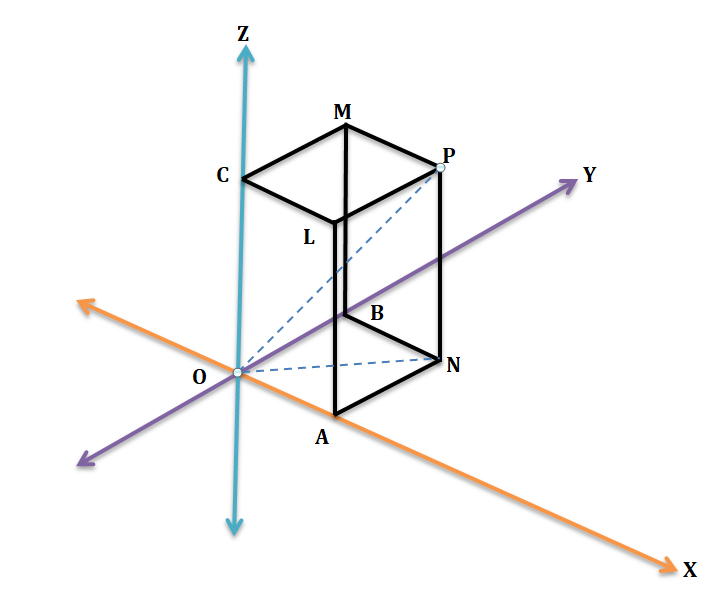
x = PM = length of the perpendicular from P on the yz-plane = AO, y = PL = length of the perpendicular from P on the zx-plane = BO, z = PN = length of the perpendicular from P on the xy-plane = CO.
On the plane YOZ, x = 0; on the plane ZOX, y = 0 and on the plane XOY, z = 0.
Thus the locus of the point for which x = 0 is the plane yz-plane; for which y = 0 is the zx-plane and for which z = 0 is the xy-plane.
If OP be the diagonal of the parallelepiped, then
\[O{{P}^{2}}=O{{N}^{2}}+N{{P}^{2}}=O{{A}^{2}}+A{{N}^{2}}+N{{P}^{2}}={{x}^{2}}+{{y}^{2}}+{{z}^{2}}\]
A plane in space divides it into two parts each of which is called half space.
Distance Between Two Points
Let the coordinates of the two points P and Q be (x1, y1, z1) and (x2, y2, z2) respectively. Then
\[PQ=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}+{{\left( {{z}_{2}}-{{z}_{1}} \right)}^{2}}}\]
Co-ordinate of a Point dividing the join of two points in a given ratio.
Let the point R divide PQ in the ratio m:n internally. Let the coordinates of P and Q be (x1, y1, z1) and (x2, y2, z2) respectively. Then the coordinates of R is
\[\left( \frac{m{{x}_{2}}+n{{x}_{1}}}{m+n},\frac{m{{y}_{2}}+n{{y}_{1}}}{m+n},\frac{m{{z}_{2}}+n{{z}_{1}}}{m+n} \right)\]
The co-ordinates of the point dividing PQ externally in the ratio m:n are
\[\left( \frac{m{{x}_{2}}-n{{x}_{1}}}{m-n},\frac{m{{y}_{2}}-n{{y}_{1}}}{m-n},\frac{m{{z}_{2}}-n{{z}_{1}}}{m-n} \right)\]
The coordinates of the middle point of PQ are
\[\left( \frac{{{x}_{1}}+{{x}_{2}}}{2},\frac{{{y}_{1}}+{{y}_{2}}}{2}.\frac{{{z}_{1}}+{{z}_{2}}}{2} \right)\]
Direction Cosines
If α, β, γ be the angles which a straight line makes with the lines parallel to the axes of coordinates, the α, β, γ are called the direction angles of the line. If α, β, γ be the angles which a straight line makes with the positive directions of the axes, then \[\cos \alpha ,\cos \beta ,\,\cos \gamma \]are called direction cosines of the line. They are generally denoted by l, m, n.
\[{{l}^{2}}+{{m}^{2}}+{{n}^{2}}={{\cos }^{2}}\alpha +{{\cos }^{2}}\beta +\,{{\cos }^{2}}\gamma =1\]
The direction cosines of the x-axis, y-axis and z-axis are, by definition (1, 0, 0), (0, 1, 0) and (0, 0, 1) respectively.
Direction Ratios
Any three numbers a, b, c which are proportional to the direction cosines l, m, n respectively of a given straight line are called the direction ratios or direction numbers of the given line.
\[\frac{l}{a}=\frac{m}{b}=\frac{n}{c}=\pm \frac{\sqrt{{{l}^{2}}+{{m}^{2}}+{{n}^{2}}}}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}=\pm \frac{1}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\]
\[\therefore \,\,l=\pm \frac{a}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}},\,\,m=\pm \frac{b}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}},\,\,n=\pm \frac{c}{\sqrt{{{a}^{2}}+{{b}^{2}}+{{c}^{2}}}}\]
Where the same sign either positive or negative is to be chosen throughout.
Direction cosines of a straight line joining two given points
Let the points P and Q be (x1, y1, z1) and (x2, y2, z2) respectively and l, m, n be the direction cosines of the straight line PQ whose direction angles are α, β, γ.
The direction ratios of the straight line joining P and Q being \left( {{x}_{2}}-{{x}_{1}} \right),\,\,\left( {{y}_{2}}-{{y}_{1}} \right),\,\,\left( {{z}_{2}}-{{z}_{1}} \right) the direction cosines are
\[\frac{{{x}_{2}}-{{x}_{1}}}{PQ},\frac{{{y}_{2}}-{{y}_{1}}}{PQ},\frac{{{z}_{2}}-{{z}_{1}}}{PQ}\]
Projections
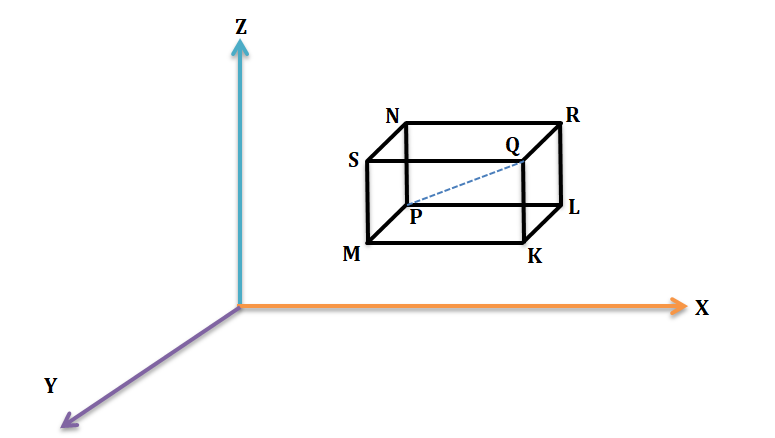
The projection of a point on any straight line is the point where the line is met by the plane through the point perpendicular to the line. Thus the foot of the perpendicular from a point on a given straight line is the projection of the point on that line. Hence, in the figure-2 A, B, C are the projections of P on the coordinates axes.
The projection of a straight line of limited length on another straight line is the length intercepted between the projections of its extremities.
Suppose we have a straight line PQ and a plane T in space. Draw Pp and Qq perpendiculars from P and Q on the plane T. Then pq is called the orthogonal projection of PQ on T. If QP is produced to meet the plane in R, then Rpq is the projection of RPQ.
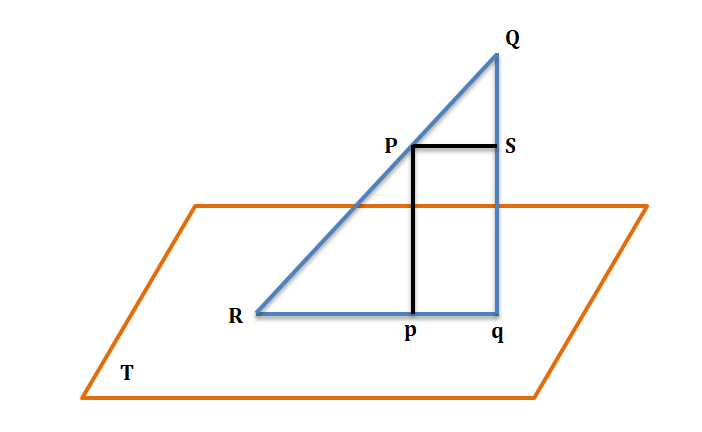
Projection of a line segment joining two points on another line.
Let the points P and Q be (x1, y1, z1) and (x2, y2, z2) respectively. Through P and Q draw planes parallel to the co-ordinate planes to form a rectangular parallelepiped.
Then clearly, AP={{x}_{2}}-{{x}_{1}},\,\,AN={{y}_{2}}-{{y}_{1}},\,\,QN={{z}_{2}}-{{z}_{1}}.
The projections of AP, AN, QN on any straight line L, whose direction cosines are l, m, n are \left( {{x}_{2}}-{{x}_{1}} \right)l,\,\,\left( {{y}_{2}}-{{y}_{1}} \right)m,\,\,\left( {{z}_{2}}-{{z}_{1}} \right)n respectively.
The projection of PQ on the straight line L is thus the sum of the projections of the components AP, AN and QN on the straight line L and is thus equal to
\[\left( {{x}_{2}}-{{x}_{1}} \right)l+\left( {{y}_{2}}-{{y}_{1}} \right)m+\,\left( {{z}_{2}}-{{z}_{1}} \right)n\]
Angle between two straight lines
Let OP and OQ be two straight lines through the origin O parallel to the two given straight lines with direction cosines \left( {{l}_{1}},\,\,{{m}_{1}},\,\,{{n}_{1}} \right) and \left( {{l}_{2}},\,\,{{m}_{2}},\,\,{{n}_{2}} \right) respectively. Let the angle between the two given straight lines, that is, the angle between OP and OQ be θ. Let P and Q be the points with coordinates (x1, y1, z1) and (x2, y2, z2) respectively.
\[\cos \theta ={{l}_{1}}{{l}_{2}}+{{m}_{1}}{{m}_{2}}+{{n}_{1}}{{n}_{2}}\]
| Example 01 |
Find the ratio in which the line segment joining the points (2, –3, 5) and (7, 1, 3) is divided by the xy-plane.
Solution:
Let the required ratio be m:n.<br>The co-ordinates of the point are \left( \frac{7m+2m}{m+n},\frac{m-3n}{m+n},\frac{3m+5n}{m+n} \right)<br>This point lies on the xy-plane. Hence its z-coordinate is zero. That is
\[\frac{3m+5n}{m+n}=0\]
\[\Rightarrow 3m+5n=0\]
\[\Rightarrow \frac{m}{n}=-\frac{5}{3}\]
Hence the division ratio is 5:3 externally.
| Example 02 |
Find the centroid of the triangle whose vertices are the points A(x1, y1, z1), B(x2, y2, z2) and C(x3, y3, z3).
Solution:
Let D be the middle point of the side BC. Therefore the co-ordinates of D are \left( \frac{{{x}_{2}}+{{x}_{3}}}{2},\frac{{{y}_{2}}+{{y}_{3}}}{2}.\frac{{{z}_{2}}+{{z}_{3}}}{2} \right)
Now, if G be the centroid, then AG:GD = 2:1.<br>Therefore, if (x, y, z) be the co-ordinates of G, then
\[x=\frac{1\times {{x}_{1}}+2\times \frac{{{x}_{2}}+{{x}_{3}}}{2}}{2+1}=\frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3}\]
\[y=\frac{1\times {{y}_{1}}+2\times \frac{{{y}_{2}}+{{y}_{3}}}{2}}{2+1}=\frac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3}\]
\[z=\frac{1\times {{z}_{1}}+2\times \frac{{{z}_{2}}+{{z}_{3}}}{2}}{2+1}=\frac{{{z}_{1}}+{{z}_{2}}+{{z}_{3}}}{3}\]
| Example 03 |
Find the projection of the line segment joining the points (3, 3, 5) and (5, 4, 3) on the straight line joining the points (2, –1, 4) and (0, 1, 5).
Solution:
The projections of the line segment joining the points (3, 3, 5) and (5, 4, 3) on the axes are (5 – 3), (4 – 3), (3 – 5) that is 2, 1, –2.
The direction cosines of the straight line joining the points (2, –1, 4) and (0, 1, 5) are -\frac{2}{3},\frac{2}{3},\frac{1}{3} since \sqrt{{{\left( 2-0 \right)}^{2}}+{{\left( -1-1 \right)}^{2}}+{{\left( 4-5 \right)}^{2}}}=3.
Hence the projection of the first line on the second line is
\[2\left( -\frac{2}{3} \right)+1\left( \frac{2}{3} \right)-2\left( \frac{1}{3} \right)=-\frac{4}{3}\]
| Example 04 |
Show that the triangle formed by the points (2, 3, 1), (–2, 2, 0) and (0, 1, –1). Find also the other angles.
Solution:
Let the given vertices be A, B, C respectively.
The direction cosines of BA, BC, CA are respectively
\[\left( \frac{4}{\sqrt{18}},\frac{1}{\sqrt{18}},\frac{1}{\sqrt{18}} \right);\left( \frac{2}{\sqrt{6}},-\frac{1}{\sqrt{6}},-\frac{1}{\sqrt{6}} \right);\left( \frac{2}{\sqrt{12}},\frac{2}{\sqrt{12}},\frac{2}{\sqrt{12}} \right)\]
The angle between BA and BC is
\[{{\cos }^{-1}}\left( \frac{8-1-1}{\sqrt{18}\sqrt{5}} \right)={{\cos }^{-1}}\frac{1}{\sqrt{13}}\]
The angle between BC and CA is
\[{{\cos }^{-1}}\left( \frac{4-2-2}{\sqrt{6}\sqrt{12}} \right)={{\cos }^{-1}}0=90{}^\circ \]
The angle between CA and BA is
\[{{\cos }^{-1}}\left( \frac{8+2+2}{\sqrt{18}\sqrt{12}} \right)={{\cos }^{-1}}\frac{2}{\sqrt{6}}\]
So the triangle is right-angled and the other angles are {{\cos }^{-1}}\frac{1}{\sqrt{3}} and {{\cos }^{-1}}\frac{2}{\sqrt{6}}.
Plane |


