Some Formulae on Pair of Straight Lines
Here are some important formulas on Pair of Straight Lines.
1. A second-degree homogeneous equation of the form ax2 + 2hxy + by2 = 0 represents a pair of straight lines through the origin if h2 ≥ ab.
2. The angle between the pair of straight lines ax2 + 2hxy + by2 = 0 are \tan \theta =\frac{2\sqrt{{{h}^{2}}-ab}}{a+b}
3. If the two straight lines be coincident, then θ = 0 and hence {{h}^{2}}-ab=0
4. If the lines be at right angles, then θ = 90° and hence a + b =0
5. The equation of bisectors of the angles between the lines ax2 + 2hxy + by2 = 0 are
\[\frac{{{x}^{2}}-{{y}^{2}}}{a-b}=\frac{xy}{h}\]
6. The equation a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0 represents a pair of straight lines if
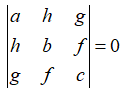
| Example 01 |
Find the value of λ, so that the equation 6{{x}^{2}}+xy+\lambda {{y}^{2}}+2x-31y-20=0 may represents a pair of straight lines.
Solution:
We have 6{{x}^{2}}+xy+\lambda {{y}^{2}}+2x-31y-20=0
Comparing it with a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0 we get,
a = 6, h = \frac{1}{2}, b = λ, g = 1, f = -\frac{31}{2}, c = –20
If the curve represents a pair of straight lines then,
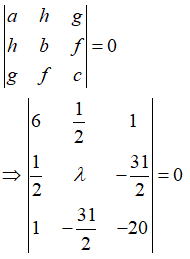
\[\Rightarrow 6\left( -20\times \lambda -\frac{31}{2}\times \frac{31}{2} \right)-\frac{1}{2}\left( -20\times \frac{1}{2}-\frac{31}{2}\times 1 \right)+1\left( -\frac{31}{2}\times \frac{1}{2}-1\times \lambda \right)=0\]
\[\Rightarrow \lambda +12=0\]
\[\therefore \,\,\lambda =-12\]
| Example 02 |
Show that the equation {{x}^{2}}+3xy+2{{y}^{2}}=0 represents a pair of straight lines. Find these straight lines and the angle between them.
Solution:
The given equation is a homogeneous equation of second degree. So, it represents a pair of straight lines through the origin.
The given equation {{x}^{2}}+3xy+2{{y}^{2}}=0 can be written as \left( x+y \right)\left( x+2y \right)=0.
Hence the two straight lines represented by the given equation are
\[x+y=0\]
\[x+2y=0\]
Comparing {{x}^{2}}+3xy+2{{y}^{2}}=0 with a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0 we get,
\[a=1, h= \frac{3}{2}, b=2, g=0, f=0, c=0\]
The angle between them is
\[{{\tan }^{-1}}\left\{ \frac{2\sqrt{{{h}^{2}}-ab}}{a+b} \right\}={{\tan }^{-1}}\left\{ \frac{2\sqrt{{{\left( \frac{3}{2} \right)}^{2}}-1\times 2}}{1+2} \right\}={{\tan }^{-1}}\left( \frac{1}{3} \right)\]
| Example 03 |
Show that the equation to the pair of straight lines through the origin perpendicular to the pair of straight lines a{{x}^{2}}+2hxy+b{{y}^{2}}=0 is b{{x}^{2}}-2hxy+a{{y}^{2}}=0.
Solution:
Let y={{m}_{1}}x and y={{m}_{2}}x be the straight lines represented by the equation a{{x}^{2}}+2hxy+b{{y}^{2}}=0, so that
\[{{m}_{1}}+{{m}_{2}}=-\frac{2h}{b},\,\,{{m}_{1}}{{m}_{2}}=\frac{a}{b}………\left( 1 \right)\]
The straight lines perpendicular to y={{m}_{1}}x and y={{m}_{2}}x passing through the origin are y=-\frac{1}{{{m}_{1}}}x and y=-\frac{1}{{{m}_{2}}}x respectively.
Hence the required pair of straight lines is
\[\left( y+\frac{1}{{{m}_{1}}}x \right)\left( y+\frac{1}{{{m}_{2}}}x \right)=0\]
\[\Rightarrow \left( {{m}_{1}}y+x \right)\left( {{m}_{2}}y+x \right)=0\]
\[\Rightarrow {{m}_{1}}{{m}_{2}}{{y}^{2}}+\left( {{m}_{1}}+{{m}_{2}} \right)xy+{{x}^{2}}=0\]
\[\Rightarrow \frac{a}{b}{{y}^{2}}-\frac{2h}{b}xy+{{x}^{2}}=0\,\,\left[ By\,\,\left( 1 \right) \right]\]
\[\Rightarrow b{{x}^{2}}-2hxy+a{{y}^{2}}=0\]
Hence the equation to the pair of straight lines through the origin perpendicular to the pair of straight lines a{{x}^{2}}+2hxy+b{{y}^{2}}=0 is b{{x}^{2}}-2hxy+a{{y}^{2}}=0.
| Example 04 |
Prove that the equation to the straight lines through the origin each of which makes an angle α with the straight lines y = x is {{x}^{2}}-2xy\sec 2\alpha +{{y}^{2}}=0.
Solution:
The slope of the straight line y = x is 1=\tan \frac{\pi }{4}.
So, the straight line makes an angle \frac{\pi }{4} with x-axis.
Hence the required straight lines makes angle \left( \frac{\pi }{4}-\alpha \right) and \left( \frac{\pi }{4}+\alpha \right) with x-axis.
As they pass through the origin, their equations are
\[y=x\tan \left( \frac{\pi }{4}-\alpha \right);\,\,y=x\tan \left( \frac{\pi }{4}+\alpha \right)\]
\[i.e.,\,y-\frac{1-\tan \alpha }{1+\tan \alpha }x=0\,\,and\,\,y-\frac{1+\tan \alpha }{1-\tan \alpha }x=0\]
Therefore the required equation of the pair of straight lines is
\[\left( y-\frac{1-\tan \alpha }{1+\tan \alpha }x \right)\left( y-\frac{1+\tan \alpha }{1-\tan \alpha }x \right)=0\]
\[\Rightarrow {{y}^{2}}-\left( \frac{1-\tan \alpha }{1+\tan \alpha }+\frac{1+\tan \alpha }{1-\tan \alpha } \right)xy+{{x}^{2}}=0\]
\[\Rightarrow {{y}^{2}}-\frac{2\left( 1+{{\tan }^{2}}\alpha \right)}{1-{{\tan }^{2}}\alpha }xy+{{x}^{2}}=0\]
\[\Rightarrow {{x}^{2}}-\frac{2}{\cos 2\alpha }xy+{{y}^{2}}=0\,\,\left[ \because \frac{1-{{\tan }^{2}}\alpha }{1-{{\tan }^{2}}\alpha }=\cos 2\alpha \right]\]
\[\Rightarrow {{x}^{2}}-2xy\sec 2\alpha +{{y}^{2}}=0\]
| Example 05 |
If the pair of straight lines {{x}^{2}}-2pxy-{{y}^{2}}=0 and {{x}^{2}}-2qxy-{{y}^{2}}=0 be such that each pair bisects the angles between the other pair, then prove that pq = –1.
Solution:
The equation of the bisectors of the angles between the pair of straight lines {{x}^{2}}-2pxy-{{y}^{2}}=0 is
\[\frac{{{x}^{2}}-{{y}^{2}}}{1-\left( -1 \right)}=\frac{xy}{-p}\]
\[\Rightarrow \frac{{{x}^{2}}-{{y}^{2}}}{2}=\frac{xy}{-p}\]
\[\Rightarrow p{{x}^{2}}-p{{y}^{2}}=-2xy\]
\[\Rightarrow p{{x}^{2}}+2xy-p{{y}^{2}}=0………\left( 1 \right)\]
But, by the condition of the problem, (1) is identical with {{x}^{2}}-2qxy-{{y}^{2}}=0. Comparing, we have
\[\frac{p}{1}=\frac{1}{-q}=\frac{p}{1}\]
\[\therefore \,\,pq=-1\,\,\left[ \text{Proved} \right]\]
| Example 06 |
Show that the angle between one of the straight lines given by a{{x}^{2}}+2hxy+b{{y}^{2}}=0 and one of the straight lines given by a{{x}^{2}}+2hxy+b{{y}^{2}}+\lambda \left( {{x}^{2}}+{{y}^{2}} \right)=0 is equal to the angle between the other two straight lines of the system.
Solution:
\[We have, a{{x}^{2}}+2hxy+b{{y}^{2}}+\lambda \left( {{x}^{2}}+{{y}^{2}} \right)=0\]
\[i.e.,\left( a+\lambda \right){{x}^{2}}+2hxy+\left( b+\lambda \right){{y}^{2}}=0\]
The equation of the bisectors of the angles between the straight lines a{{x}^{2}}+2hxy+b{{y}^{2}}=0 is
\[\frac{{{x}^{2}}-{{y}^{2}}}{a-b}=\frac{xy}{h}\]
Also, the equation of the bisectors of the angles between the straight lines i.e.,\left( a+\lambda \right){{x}^{2}}+2hxy+\left( b+\lambda \right){{y}^{2}}=0 is
\[\frac{{{x}^{2}}-{{y}^{2}}}{\left( a+\lambda \right)-\left( b+\lambda \right)}=\frac{xy}{h}\]
\[\Rightarrow \frac{{{x}^{2}}-{{y}^{2}}}{a-b}=\frac{xy}{h}\]
Thus the two pairs have the same bisectors.
| Example 07 |
Find the condition that one of the straight lines given by a{{x}^{2}}+2hxy+b{{y}^{2}}=0 may coincide with one of the straight lines given by a'{{x}^{2}}+2h'xy+b'{{y}^{2}}=0.
Solution:
Let the two pairs have a common straight line y=mx.
Then substituting mx of y in the two equations and cancelling x2, we have
\[a+2hm+b+{{m}^{2}}=0\]
\[a’+2h’m+b'{{m}^{2}}=0\]
Therefore by cross-multiplication, we get
\[\frac{{{m}^{2}}}{ah’-a’h}=\frac{2m}{ba’-b’a}=\frac{1}{hb’-h’b}\]
\[\Rightarrow \frac{{{m}^{2}}}{m}=\frac{2\left( ah’-a’h \right)}{ba’-b’a};\,m=\frac{ba’-b’a}{2\left( hb’-h’b \right)}\]
\[\Rightarrow m=\frac{2\left( ah’-a’h \right)}{ba’-b’a};\,m=\frac{ba’-b’a}{2\left( hb’-h’b \right)}\]
\[\therefore \frac{2\left( ah’-a’h \right)}{ba’-b’a}=\frac{ba’-b’a}{2\left( hb’-h’b \right)}\]
\[\Rightarrow 4\left( ah’-a’h \right)\left( hb’-h’b \right)={{\left( ba’-b’a \right)}^{2}}\]
This is the required condition.
| Example 08 |
The gradient of one of the straight lines of a{{x}^{2}}+2hxy+b{{y}^{2}}=0 is twice that of the other. Show that 8{{h}^{2}}=9ab.
Solution:
Let the two straight lines be y={{m}_{1}}x and y={{m}_{2}}x
Then substituting mx of y in the two equations and canceling x2, we have
\[\therefore \,2{{m}_{2}}+{{m}_{2}}=-\frac{2h}{b}\,\,and\,2{{m}_{2}}\times {{m}_{2}}=\frac{a}{b}\,\]
\[\Rightarrow 3{{m}_{2}}=-\frac{2h}{b}\,\,and\,2m_{2}^{2}=\frac{a}{b}\,\]
\[\Rightarrow {{m}_{2}}=-\frac{2h}{3b}\,\,and\,m_{2}^{2}=\frac{a}{2b}\,\]
\[\therefore \,{{\left( -\frac{2h}{3b} \right)}^{2}}=\frac{a}{2b}\,\]
\[\Rightarrow \frac{4{{h}^{2}}}{9{{b}^{2}}}=\frac{a}{2b}\,\]
\[\therefore \,\,8{{h}^{2}}=9ab\,\,\left[ \text{Proved} \right]\]
| Example 09 |
Prove that the product of the perpendiculars from the point (x1, y1) on the straight lines a{{x}^{2}}+2hxy+b{{y}^{2}}=0 is \frac{ax_{1}^{2}+2h{{x}_{1}}{{y}_{1}}+by_{1}^{2}}{\sqrt{{{\left( a-b \right)}^{2}}+4{{h}^{2}}}}.
Solution:
Let the equation a{{x}^{2}}+2hxy+b{{y}^{2}}=0 represent two straight lines OA and OB passing through the origin, whose equations are
\[y-{{m}_{1}}x=0………\left( 1 \right)\]
\[y-{{m}_{2}}x=0………\left( 2 \right)\]
So that,
\[{{m}_{1}}+{{m}_{2}}=-\frac{2h}{b},\,\,{{m}_{1}}{{m}_{2}}=\frac{a}{b}………\left( 3 \right)\]
PL = p1 = Length of the perpendicular from P(x1, y1) upon OA = \left| \frac{{{y}_{1}}-{{m}_{1}}{{x}_{1}}}{\sqrt{1+m_{1}^{2}}} \right|
And PM = p2 = Length of the perpendicular from P(x1, y1) upon OB = \left| \frac{{{y}_{1}}-{{m}_{2}}{{x}_{1}}}{\sqrt{1+m_{2}^{2}}} \right|
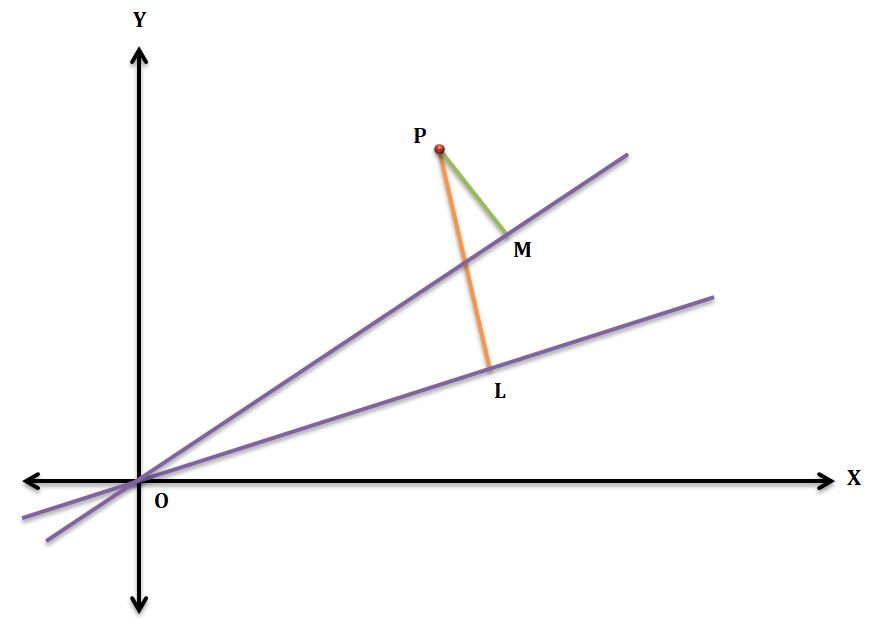
Hence the product of perpendiculars = p1 × p2
\[\left| \frac{\left( {{y}_{1}}-{{m}_{1}}{{x}_{1}} \right)\left( {{y}_{1}}-{{m}_{2}}{{x}_{1}} \right)}{\sqrt{1+m_{1}^{2}}\sqrt{1+m_{2}^{2}}} \right|\]
\[=\left| \frac{y_{1}^{2}-\left( {{m}_{1}}+{{m}_{2}} \right){{x}_{1}}{{y}_{1}}+{{m}_{1}}{{m}_{2}}x_{1}^{2}}{\sqrt{1+m_{1}^{2}+m_{2}^{2}+{{\left( {{m}_{1}}{{m}_{2}} \right)}^{2}}}} \right|\]
\[=\left| \frac{y_{1}^{2}-\left( {{m}_{1}}+{{m}_{2}} \right){{x}_{1}}{{y}_{1}}+{{m}_{1}}{{m}_{2}}x_{1}^{2}}{\sqrt{1+{{\left( {{m}_{1}}+{{m}_{2}} \right)}^{2}}-2{{m}_{1}}{{m}_{2}}+{{\left( {{m}_{1}}{{m}_{2}} \right)}^{2}}}} \right|\]
\[=\left| \frac{y_{1}^{2}-\left( -\frac{2h}{b} \right){{x}_{1}}{{y}_{1}}+\left( \frac{a}{b} \right)x_{1}^{2}}{\sqrt{1+{{\left( -\frac{2h}{b} \right)}^{2}}-2\frac{a}{b}+{{\left( \frac{a}{b} \right)}^{2}}}} \right|\]
\[=\frac{ax_{1}^{2}+2h{{x}_{1}}{{y}_{1}}+by_{1}^{2}}{\sqrt{{{\left( a-b \right)}^{2}}+4{{h}^{2}}}}\,\,\left[ \text{Proved} \right]\]
General Equation |
Circle |


