General Equation of Second Degree
The general equation of second degree is a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0. The curve represented by this equation is a conic section or conic.
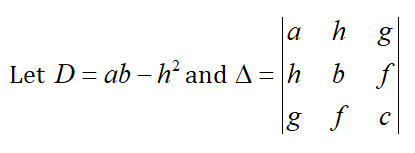
The nature of the conic is represented by these two quantities,
Nature of Conic
| Type | \[D=ab-{{h}^{2}}\] | △ | Canonical form | Name |
| Elliptic | D > 0 | △< 0 | \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\] | Ellipse |
| D > 0 | △ < 0 | \[{{x}^{2}}+{{y}^{2}}={{a}^{2}}\] | Circle | |
| D > 0 | △ > 0 | \[\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=-1\] | Imaginary Ellipse | |
| D > 0 | △ = 0 | \[{{a}^{2}}{{x}^{2}}+{{b}^{2}}{{y}^{2}}=0\] | Pair of imaginary lines or point ellipse | |
| Parabolic | D = 0 | △ ≠ 0 | {{x}^{2}}=4ay or {{y}^{2}}=4ax | Parabola |
| D = 0 | △ = 0 | \[{{x}^{2}}={{a}^{2}}\,or\,{{y}^{2}}={{b}^{2}}\] | Pair of parallel lines | |
| D = 0 | △ = 0 | \[{{x}^{2}}=0\,\,or\,{{y}^{2}}=0\] | Pair of coincident lines | |
| Hyperbolic | D < 0 | △ < 0 | \[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=-1\] | Hyperbola |
| D < 0 | △ = 0 | \[{{x}^{2}}-{{k}^{2}}{{y}^{2}}=0\] | Pair of intersecting lines | |
| D < 0 | △ > 0 | \[\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\] | hyperbola |
| Example 01 |
What conics do the following equations represent?
\[\left( i \right)\,{{x}^{2}}+2xy+{{y}^{2}}-2x-1=0\]
\[\left( ii \right)\,2{{x}^{2}}+3{{y}^{2}}-4x+5y+4=0\]
\[\left( iii \right)\,{{x}^{2}}+4xy+{{y}^{2}}-2x+2y-6=0\]
Solution:
(i) We have {{x}^{2}}+2xy+{{y}^{2}}-2x-1=0
Comparing it with a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0 we get,
a = 1, h = 1, b = 1, g = –1, f = 0, c = –1
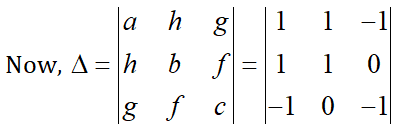
\[=1\left( -1-0 \right)-1\left( -1-0 \right)-1\left( 0+1 \right)\]
\[=-1+1-1=-1\ne 0\]
\[Also, D=ab-{{h}^{2}}=1\times 1-{{\left( -1 \right)}^{2}}=0\]
Hence the given conic is a parabola.
(ii) We have 2{{x}^{2}}+3{{y}^{2}}-4x+5y+4=0
Comparing it with a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0 we get,
a = 2, h = 0, b = 3, g = –2, f = \frac{5}{2}, c = 4
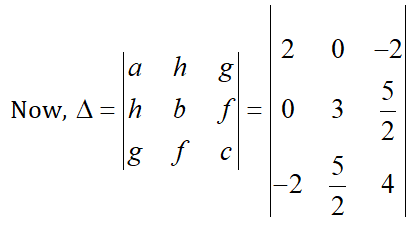
\[=2\left( 3\times 4-\frac{5}{2}\times \frac{5}{2} \right)-0\left( 0\times 4+2\times \frac{5}{2} \right)-2\left( 0\times \frac{5}{2}+2\times 3 \right)\]
\[=2\left( 12-\frac{25}{4} \right)-0-2\left( 6 \right)\]
\[=2\times \frac{23}{4}-12=-\frac{1}{2}<0\]
\[Also, D=ab-{{h}^{2}}=2\times 3-{{\left( 0 \right)}^{2}}=6>0\]
Hence, the given conic is an ellipse.
(iii) We have {{x}^{2}}+4xy+{{y}^{2}}-2x+2y-6=0
Comparing it with a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0 we get,
a = 1, h = 2, b = 1, g = –1, f = 1, c = –6
\[Now, D=ab-{{h}^{2}}=1\times 1-{{\left( 2 \right)}^{2}}=1-4=-3<0\]
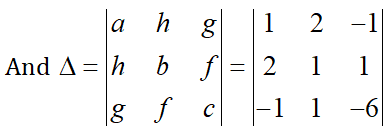
\[=1\left( -6\times 1-1\times 1 \right)-2\left( -6\times 2+1\times 1 \right)-1\left( 2\times 1+1\times 1 \right)\]
\[=\left( -7 \right)-2\left( -11 \right)-\left( 3 \right)\]
\[=-7+22-3=12>0\]
Hence, the given conic is a hyperbola.
| Example 02 |
If the equation 13{{x}^{2}}+10xy+b{{y}^{2}}-62\sqrt{2}x-46\sqrt{2}y+170=0 represents a point ellipse, find the value of b and the point.
Solution:
We have 13{{x}^{2}}+10xy+b{{y}^{2}}-62\sqrt{2}x-46\sqrt{2}y+170=0
Comparing it with a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0 we get,
a = 13, h = 5, g = -31\sqrt{2}, f =-23\sqrt{2}, c = 170
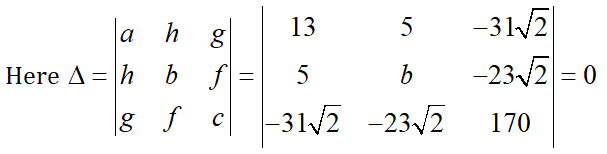
\[\Rightarrow 13\left( 170b-1058 \right)-5\left( 850-1426 \right)-31\sqrt{2}\left( -115\sqrt{2}+31\sqrt{2}b \right)=0\]
\[\Rightarrow 2210b-13754-4250+7130+7130-1922b=0\]
\[\Rightarrow 288b-3744=0\]
\[\therefore \,\,\,b=13\]
\[Again, D=ab-{{h}^{2}}=13\times 13-{{\left( 5 \right)}^{2}}=169-25=144>0\]
Therefore, the equation represents a point ellipse when b = 13.
The point is the center. If (α, β) be the center, then
\[13\alpha +5\beta -31\sqrt{2}=0,\,\,\,5\alpha +13\beta -23\sqrt{2}=0\]
\[Solving\,\,\alpha =2\sqrt{2},\,\,\beta =\sqrt{2}\]
Thus the point is \left( 2\sqrt{2},\sqrt{2} \right).
| Example 03 |
Discuss the nature of the conic represented by 3{{x}^{2}}-8xy-3{{y}^{2}}+10x-13y+8=0.
Solution:
We have 3{{x}^{2}}-8xy-3{{y}^{2}}+10x-13y+8=0
Comparing it with a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0 we get,
a = 3, h = –4, b= –3, g = 5, f =-\frac{13}{2}, c = 8
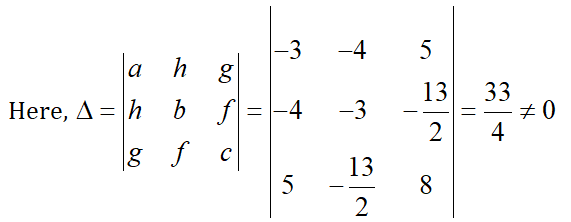
\[D=ab-{{h}^{2}}=3\times \left( -3 \right)-{{\left( -4 \right)}^{2}}=-9-16=-25<0\]
Therefore, the equation represents a hyperbola.
Again coefficient of x2 + coefficient of y2 = 3 – 3 = 0
Therefore the hyperbola is rectangular.
| Example 04 |
Find the center of the ellipse 7{{x}^{2}}-2xy+7{{y}^{2}}+22x-10y+7=0.
Solution:
We have 7{{x}^{2}}-2xy+7{{y}^{2}}+22x-10y+7=0
Comparing it with a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0 we get,
a = 7, h = –1, b= 7, g = 11, f = –5, c = 7
Let the center be (α, β) and it is obtained from the equations
\[a\alpha +h\beta +g=0\]
\[h\alpha +b\beta +f=0\]
Therefore we have
\[7\alpha -\beta +11=0\]
\[-\alpha +7\beta -5=0\]
Solving the above equations we get \alpha =-\frac{3}{2},\,\,\beta =\frac{1}{2}
Therefore, the center of the conic is \left( -\frac{3}{2},\frac{1}{2} \right).
| Example 05 |
Show that the curve 4{{x}^{2}}+4xy+{{y}^{2}}+4x+2y+20=0 has infinitely many centers.
Solution:
We have 4{{x}^{2}}+4xy+{{y}^{2}}+4x+2y+20=0
Comparing it with a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0 we get,
a = 4, h = 2, b= 1, g = 2, f = 1, c = 20
Let the center be (α, β) and it is obtained from the equations
\[a\alpha +h\beta +g=0\]
\[h\alpha +b\beta +f=0\]
Therefore we have
\[4\alpha +2\beta +2=0\]
\[2\alpha +\beta +1=0\]
The above two equations are identical and they are 2\alpha +\beta +1=0.
These equations have an infinite solution.
Thus the given conic has infinitely many centers.
| Example 06 |
Find the nature of the conic 6{{x}^{2}}-5xy-6{{y}^{2}}+14x+5y+4=0.
Solution:
We have 6{{x}^{2}}-5xy-6{{y}^{2}}+14x+5y+4=0
Comparing it with a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0 we get,
a = 6, h = -\frac{5}{2}, b= –6, g = 7, f = \frac{5}{2}, c = 4
\[Here, D=ab-{{h}^{2}}=6\times \left( -6 \right)-{{\left( -\frac{5}{2} \right)}^{2}}=-36-\frac{25}{4}=-\frac{169}{4}<0\]
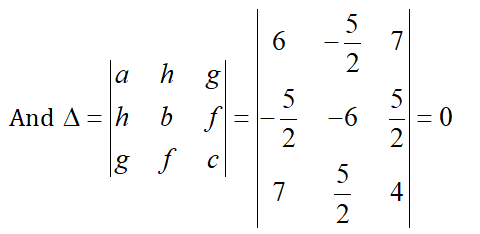
Hence the given conic is a pair of intersecting lines.
Transformation of Rectangular Axes |
Pair of Straight Lines |


