General Equation of the Second Degree
The surface represented by a general equation of the second degree in x, y, z is called a second-order surface.
The general equation of the second degree in x, y, z is usually written in the form:
\[a{{x}^{2}}+b{{y}^{2}}+c{{z}^{2}}+2hxy+2fyz+2gzx+2ux+2vy+2wz+d=0………\left( 1 \right)\]
Hence (1) represents a second order surface. Such a surface is sometimes called a quadratic surface or simply a quadratic or a conicoid.
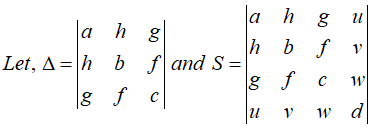
Then S=-u\left( Au+Hv+Gw \right)-v\left( Hu+Bv+Fw \right)-w\left( Gu+Fv+Cw \right)+d\Delta
Where A, B, C, F, G, H are the cofactors of a, b, c, f, g, h respectively in △.
A complete classification of quadrics according to different possible values of △ and S, the corresponding canonical forms and their corresponding names are given bellow in tabular form.
| △ | S | Canonical form | Name |
| ≠ 0 | < 0 | \[\frac{{{x}^{2}}}{{{\alpha }^{2}}}+\frac{{{y}^{2}}}{{{\beta }^{2}}}+\frac{{{z}^{2}}}{{{\gamma }^{2}}}=1\] | Ellipsoid |
| ≠ 0 | = 0 | \[\frac{{{x}^{2}}}{{{\alpha }^{2}}}+\frac{{{y}^{2}}}{{{\beta }^{2}}}+\frac{{{z}^{2}}}{{{\gamma }^{2}}}=0\] | Point-ellipsoid |
| ≠ 0 | > 0 | \[\frac{{{x}^{2}}}{{{\alpha }^{2}}}+\frac{{{y}^{2}}}{{{\beta }^{2}}}+\frac{{{z}^{2}}}{{{\gamma }^{2}}}=1\] | No Geometric Locus |
| ≠ 0 | > 0 | \[\frac{{{x}^{2}}}{{{\alpha }^{2}}}+\frac{{{y}^{2}}}{{{\beta }^{2}}}-\frac{{{z}^{2}}}{{{\gamma }^{2}}}=1\] | Hyperboloid of one sheet |
| ≠ 0 | < 0 | \[\frac{{{x}^{2}}}{{{\alpha }^{2}}}-\frac{{{y}^{2}}}{{{\beta }^{2}}}-\frac{{{z}^{2}}}{{{\gamma }^{2}}}=1\] | Hyperboloid of two sheets |
| \[\frac{{{x}^{2}}}{{{\alpha }^{2}}}+\frac{{{y}^{2}}}{{{\beta }^{2}}}-\frac{{{z}^{2}}}{{{\gamma }^{2}}}=0\]≠ 0 | = 0 | \[\frac{{{x}^{2}}}{{{\alpha }^{2}}}+\frac{{{y}^{2}}}{{{\beta }^{2}}}-\frac{{{z}^{2}}}{{{\gamma }^{2}}}=0\] | Quadric Cone |
| = 0 | > 0 | \[\frac{{{x}^{2}}}{{{\alpha }^{2}}}+\frac{{{y}^{2}}}{{{\beta }^{2}}}=2cz\] | Elliptic Paraboloid |
| = 0 | < 0 | \[\frac{{{x}^{2}}}{{{\alpha }^{2}}}-\frac{{{y}^{2}}}{{{\beta }^{2}}}=2cz\] | Hyperbolic Paraboloid |
| = 0 | = 0 | \[\frac{{{x}^{2}}}{{{\alpha }^{2}}}+\frac{{{y}^{2}}}{{{\beta }^{2}}}=1\] | Elliptic Cylinder |
| = 0 | = 0 | \[\frac{{{x}^{2}}}{{{\alpha }^{2}}}-\frac{{{y}^{2}}}{{{\beta }^{2}}}=1\] | Hyperbolic Cylinder |
| = 0 | = 0 | \[\frac{{{x}^{2}}}{{{\alpha }^{2}}}+\frac{{{y}^{2}}}{{{\beta }^{2}}}=-1\] | Non Geometric locus (imaginary cylinder) |
| = 0 | = 0 | \[\frac{{{x}^{2}}}{{{\alpha }^{2}}}+\frac{{{y}^{2}}}{{{\beta }^{2}}}=0\] | Non Geometric Locus (pair of imaginary planes with real intersection) |
| = 0 | = 0 | \[\frac{{{x}^{2}}}{{{\alpha }^{2}}}-\frac{{{y}^{2}}}{{{\beta }^{2}}}=0\] | Pair of Intersecting planes |
| = 0 | = 0 | \[{{x}^{2}}=2py,\,\,p\ne 0\] | Parabolic Cylinder |
| = 0 | = 0 | \[{{x}^{2}}-{{\alpha }^{2}}=0,\,\,\alpha \ne 0\] | Pair of parallel planes |
| = 0 | = 0 | \[{{x}^{2}}+{{\alpha }^{2}}=0,\,\,\alpha \ne 0\] | No Geometric Locus (Pair of imaginary parallel planes) |
| = 0 | = 0 | \[{{x}^{2}}=0\] | Pair of Coincident planes |
| Example 01 |
For each of the following quadrics determine whether it has a single center, no center, a line of centers or a plane of centers.
\[\left( i \right)\,\,{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2xy-2yz-2zx-2x-4y-2z-3=0\]
\[\left( ii \right)\,\,{{x}^{2}}+{{y}^{2}}+{{z}^{2}}-2xy-2yz+2zx-2x-4y-2z+3=0\]
Solution:
(i) Comparing the given equation with the general equation of the second degree in x, y, z
\[a{{x}^{2}}+b{{y}^{2}}+c{{z}^{2}}+2hxy+2fyz+2gzx+2ux+2vy+2wz+d=0\]
We have, a=1,b=1,c=1,h=-1,g=-1,f=-1,f=-1,u=-1,v=-2,w=-1,d=-3
We now consider the system of equations
ax+hy+gz+u=0,\,\,hx+by+fz+v=0,\,\,gx+fy+cz+w=0 which takes the form
\[x-y-z-1=0,\,\,-x+y-z-2=0,\,\,-x-y+z-1=0\]
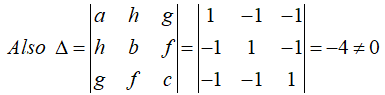
Hence the above system of equations has a unique solution namely \left( -\frac{3}{2},-1,-\frac{3}{2} \right). So the given quadric has a single center namely \left( -\frac{3}{2},-1,-\frac{3}{2} \right).
(ii) Comparing the given equation with the general equation of the second degree in x, y, z
\[a{{x}^{2}}+b{{y}^{2}}+c{{z}^{2}}+2hxy+2fyz+2gzx+2ux+2vy+2wz+d=0\]
We have, a=1,b=1,c=1,h=-1,g=1,f=-1,f=-1,u=-1,v=-2,w=-1,d=3
We now consider the system of equations
ax+hy+gz+u=0,\,\,hx+by+fz+v=0,\,\,gx+fy+cz+w=0 which takes the form x-y+z-1=0,\,\,-x+y-z-2=0,\,\,x-y+z-1=0
Since the first and the third equations of the system are the same, we have to consider the system given by
\[x-y+z-1=0,\,\,-x+y-z-2=0\]
\[i.e.,\,\,the\,\,system\,\,x-y+z-1=0,\,\,x-y+z-2=0\]
This system has no solution as the planes represented by them are parallel.
Hence the given quadric has no center.
| Example 02 |
Find the nature of the quadric represented by \[{{y}^{2}}+4zx+2x-4y+6z+5=0\]
Solution:
Comparing the given equation with the general equation of the second degree in x, y, z
\[a{{x}^{2}}+b{{y}^{2}}+c{{z}^{2}}+2hxy+2fyz+2gzx+2ux+2vy+2wz+d=0\]
We have, a=0,b=2,c=0,h=0,g=2,f=0,f=-1,u=1,v=-2,w=3,d=5
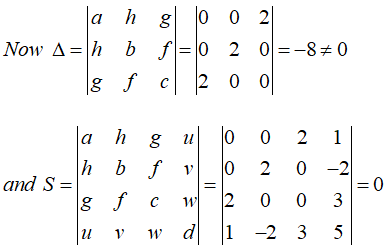
Hence the given quadric represents a cone.
Sphere |
Reduction |


