Table of Contents
In our daily life, angle is very common and its necessity is infinite. Angles are made where the two walls of the house or the two edges of the table meet. Here in this article we will discuss about angle, 15 types of angles and Systems of Measuring Angles – Sexagesimal System, Circular System.
Definition of Angle
The geometric figure formed when two straight lines intersect at a point is called an angle.
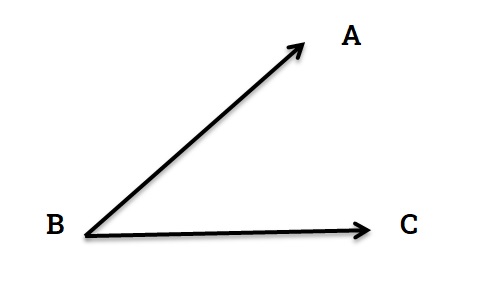
In the following figure ∠ABC is the angle
Systems of Measuring Angles
Angles are usually measured in two ways:
- Sexagesimal System
- Circular System
Sexagesimal System
In this system the unit of measure of an angle is degrees, minutes and seconds.
60 seconds (60”) = 1 minute (1′)
60 minutes (60′) = 1 degree (1°)
90 degree (90°) = 1 right angle
Circular System.
In this System, an angle is measured in radians. 1° = π/180 radian. So, x° = xπ/180 radian.
| Degrees | Radians |
| 0° | 0 |
| 30° | π/6 |
| 45° | π/4 |
| 60° | π/3 |
| 90° | π/2 |
| 120° | 2π/3 |
| 135° | 3π/4 |
| 150° | 5π/6 |
| 180° | π |
| 270° | 3π/2 |
| 360° | 2π |
Parts of an Angle
The angle is basically two parts – the arm of the angle, the vertex of the angle.
Arm of an Angle
The two straight lines forming the angle are called the arm of the angle.
In figure 2 AB and BC are the arms of the angle ABC
Vertex of an Angle
The point at which two segments meet when generating an angle is called the vertex of the angle.
In figure 2 B is the vertex of the angle ABC

Properties of Angle
- The measurement of the angle depends on the position of the arms, not on the length.
- A segment cannot generate an angle, requiring at least two segments.
- The basic unit of angle measurement is the degree.
Classification of Angles
Angles can be divided according to the variety of measurements and positions
Right angle
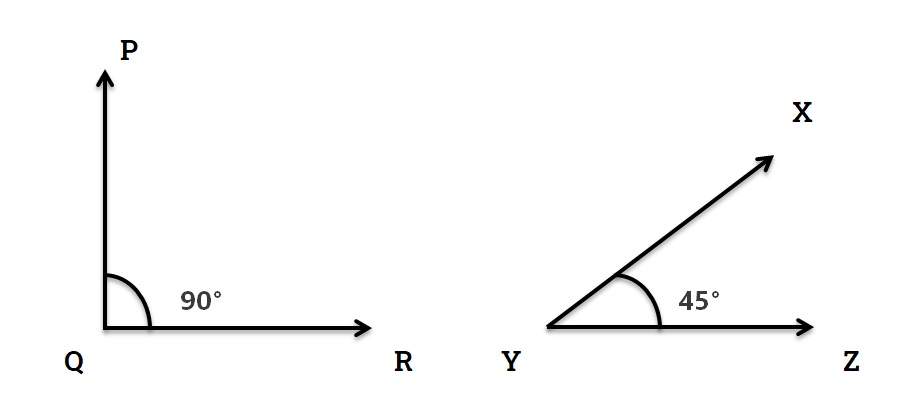
The two adjacent angles that a straight line produces by standing on another straight line are called right angles if they are equal to each other. Each of them measures 90°.
In figure 3 ∠PQR is an example of right angle.
Acute Angle
Angles smaller than one right angle are called acute angles. That is, angles smaller than 90° are acute angles.
In figure 3 ∠XYZ is an acute angle.
Obtuse angle
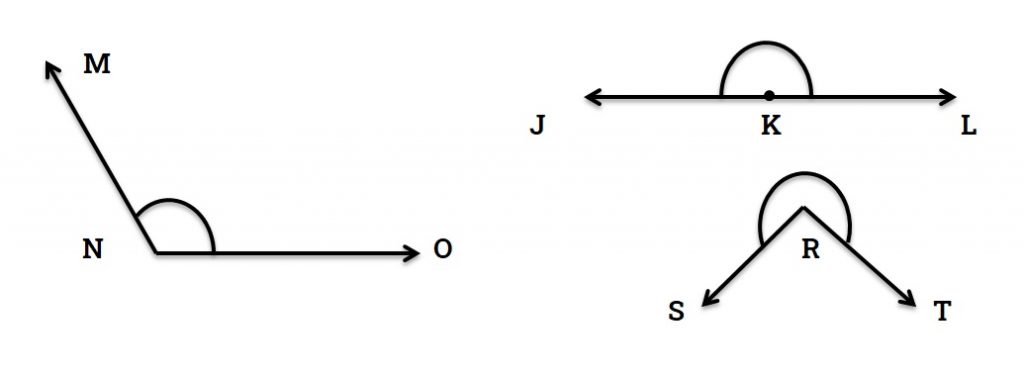
Angles larger than one right angle (90°) but smaller than two right angles (180°) are called obtuse angles.
In figure 4 ∠MNO is an obtuse angle.
Straight Angle
An angle whose value is equal to two right angles (180°) is called a straight angle.
In figure 4 ∠JKL is a straight angle.
Reflex Angle
An angle whose value is greater than two right angles (180°) but smaller than four right angles (360°) is called a reflex angle.
In figure 4 ∠SRT is a reflex angle.
Complementary angle
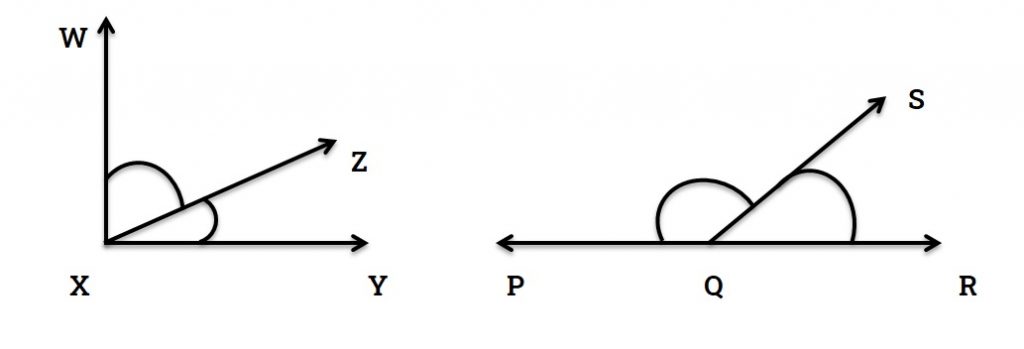
If the sum of two angles is equal to one right angle (90°), then one of them is called complementary angle to the other.
In figure 5 ∠WXZ and ∠ZXY are complementary angles as ∠WXZ + ∠ZXY = 90°
Supplementary Angle
If the sum of two angles is equal to two right angles (180°), then one of them is called supplementary angle of the other.
In figure 5 ∠PQS and ∠SQR are supplementary angles as ∠PQS + ∠SQR = 180°
Adjacent angles
If two angles have a common arm and one common vertex and the two angles are opposite to that common arm, then those two angles are called adjacent angles.
∠PQS and ∠RQS are adjacent angles in figure 6.
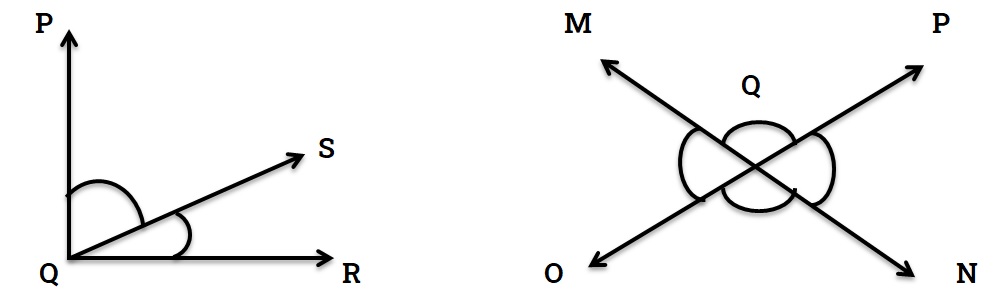
Opposite angle
When two straight lines intersect each other, the four angles that are formed on the opposite side of the point of intersection are called opposite angles.
In figure 6 ∠MQO and ∠PQN are opposite angles similarly ∠MQP and ∠OQN are opposite angles.
Inner Angle
The inner angle formed by two straight lines is called the inner angle.
∠SQR is an example of inner angle in figure 7.
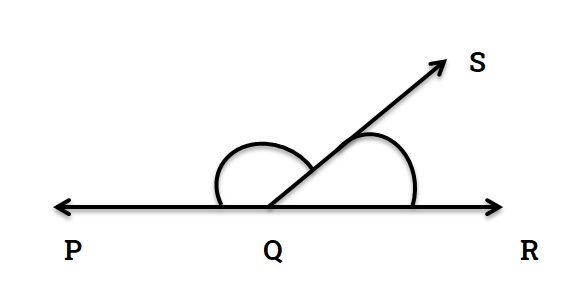
Outer Angle
The angle formed by extending one of the arms of an angle towards the vertex is called the outer angle.
∠SQP is an example of outer angle in figure 7.
Interior Angle
The eight angles that are formed when two straight lines intersect a straight line, their four angles are located in the area between the two straight lines, are called their inner angles.
∠AGH, ∠CHG, ∠BGH and ∠DHG are the interior angles in figure 8.
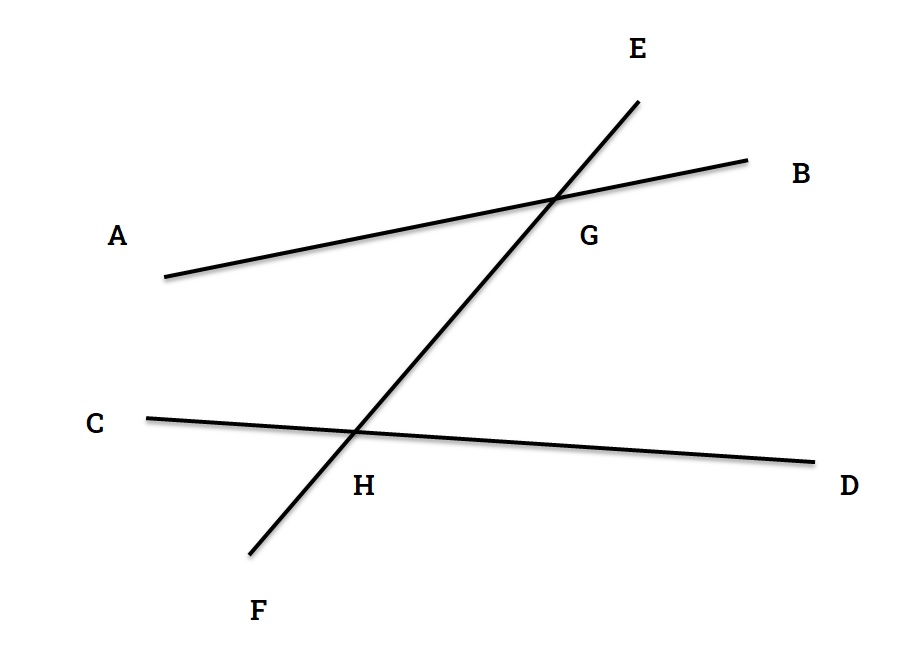
Exterior Angle
The eight angles that are formed when two straight lines intersect a straight line, their four angles are not located in the area between the two straight lines, they are called outer angles.
∠AGE, ∠CHF, ∠EGB and ∠DHF are the outer angles in the figure 8.
Alternate Angle
The eight angles that a traversal produces when it intersects two other straight lines, the angles between the straight lines which are opposite to the intersection and facing each other are called alternate angles.
∠AGH and ∠DHG are alternate angles similarly ∠BGH and ∠GHC are alternate angles in figure 9.
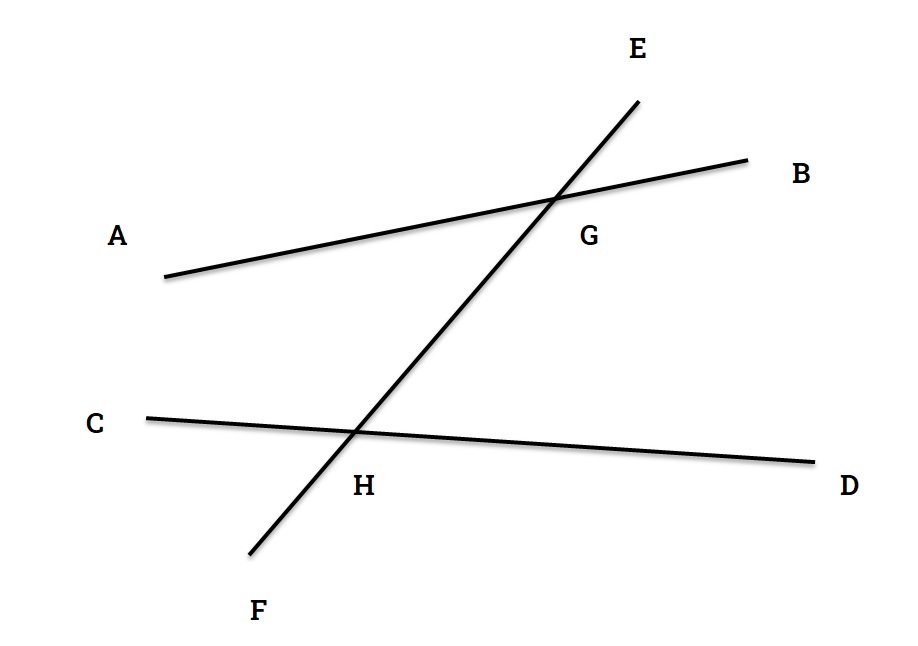
Corresponding Angles
Angles that are on the same side of the traversal and face each other in the same direction are called corresponding angles.
∠AGE and ∠CHG are corresponding angles similarly ∠AGH and ∠FHC are corresponding angles in figure 9.
Traversal
A straight line or segment that intersects two or more straight lines is called a traversal.
EF is a traversal in figure 9.
Angle bisector
A straight line passing through the vertex of an angle divides the angle into two equal parts, is called the bisector of that angle.
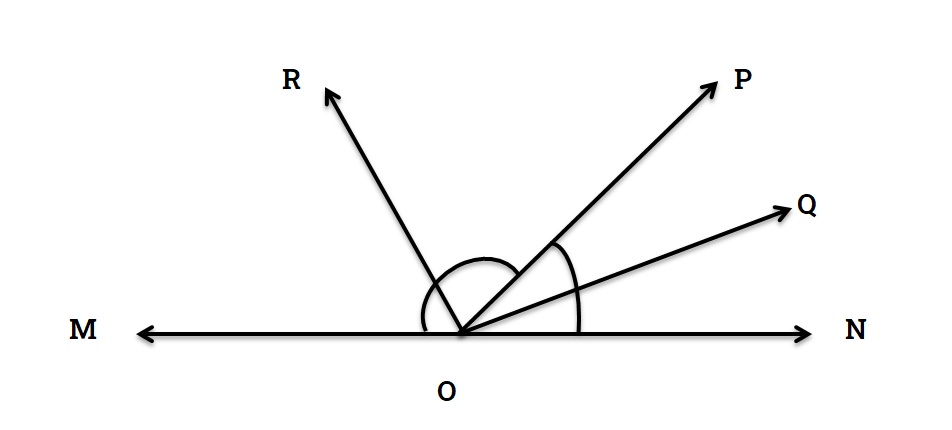
Internal Bisector
The straight line which bisects interior angle is called internal bisector.
In figure 10, OQ is internal bisector of ∠PON
External Bisector
The straight line which bisects exterior angle is called external bisector.
In figure 10, OR is external bisector of ∠PON
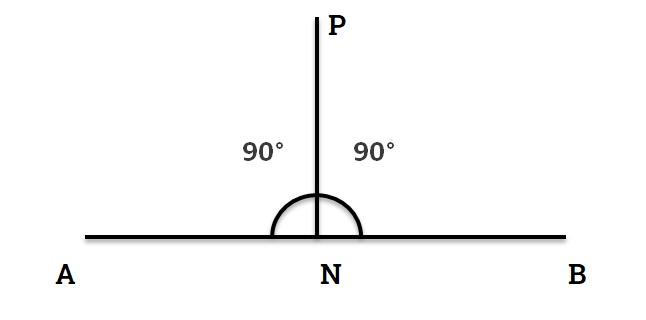
Perpendicular
If a straight line is standing on another straight line, then the two adjacent angles that are formed are equal to each other, then one of the two straight lines is called perpendicular to the other.
In figure 11, PN is perpendicular upon AB.
Always Remember
- Angles are always measured anticlockwise.
- If two straight lines are parallel to each other, their alternating angles and corresponding angles will be equal to each other.
- 1 right angle = 90°
- 1 straight angle = 180°
- A total of 360 angles can be generated at one point.
- Numerous angles can be drawn at one point.
Point Definition |
7 Types of Triangle |


