দশম শ্রেণী – তৃতীয় অধ্যায় : বৃত্ত সম্পর্কিত উপপাদ্য সম্পূর্ণ সমাধান

কষে দেখি – 3.1

1. পাশের O কেন্দ্রীয় বৃত্তের ছবি দেখি এবং কোন কোন ব্যাসার্ধ PAQ বৃত্তাংশে অবস্থিত লিখি।

2. নীচের ______ -এ বুঝে লিখি –

(i) একটি বৃত্তে _____ বিন্দু আছে।

উত্তর – অসংখ্য

(ii) বৃত্তের বৃহত্তম জ্যা_____।

উত্তর – ব্যাস

(iii) জ্যা বৃত্তাকার ক্ষেত্রকে দুটি _____ বিভক্ত করে

উত্তর – বৃত্তাংশে

(iv) বৃত্তের সকল ব্যাস _____ বিন্দুগামী।

উত্তর – কেন্দ্র

(v) দুটি বৃত্তাংশ সমান হলে তাদের বৃত্তচাপ দুটির দৈর্ঘ্য _____ হবে।

উত্তর – সমান

(vi) একটি বৃত্তাকার ক্ষেত্রের বৃত্তকলা হলো বৃত্তচাপ এবং দুটি _____ -এর দ্বারা সীমাবদ্ধ অঞ্ছল।

উত্তর – ব্যাসার্ধ

(vii) বৃত্তের বাইরের কোনো বিন্দু ও কেন্দ্রের সংযোজক রেখাংশের দৈর্ঘ্য ব্যাসার্ধের দৈর্ঘ্য অপেক্ষা _____।

উত্তর – বড়ো

3. স্কেল ও পেনসিল কম্পাসের সাহায্যে একটি বৃত্ত এঁকে কেন্দ্র, জ্যা, ব্যাস, ব্যাসার্ধ, উপচাপ, অধিচাপ নির্দেশ করি।

উত্তর – চিত্রে বৃত্তটির কেন্দ্র O, PQ জ্যা, AB ব্যাস, OR ব্যাসার্ধ,  PMQ উপচাপএবং PNQ অধিচাপ।

4. সত্য না মিথ্যা লিখি –

(i) বৃত্ত একটি সামতলিক চিত্র।
(ii) বৃত্তাংশ (Segment) একটি সামতলিক ক্ষেত্র।
(iii) বৃত্তকলা (Sector) একটি সামতলিক ক্ষেত্র।
(iv) জ্যা একটি সরলরেখাংশ।
(v) চাপ একটি সরলরেখাংশ।
(vi) একটি বৃত্তে সসীম সংখ্যক একই দৈর্ঘ্যের জ্যা আছে।
(vii) একটি নির্দিষ্ট বিন্দুকে কেন্দ্র করে একটিই বৃত্ত আঁকা সম্ভব।
(viii) দুটি সর্বসম বৃত্তের ব্যাসার্ধের দৈর্ঘ্য সমান।

উত্তর –

(i) বৃত্ত একটি সামতলিক চিত্র – সত্য।

(ii) বৃত্তাংশ (Segment) একটি সামতলিক ক্ষেত্র – সত্য।

(iii) বৃত্তকলা (Sector) একটি সামতলিক ক্ষেত্র – সত্য।

(iv) জ্যা একটি সরলরেখাংশ – সত্য।

(v) চাপ একটি সরলরেখাংশ – মিথ্যা।

(vi) একটি বৃত্তে সসীম সংখ্যক একই দৈর্ঘ্যের জ্যা আছে – মিথ্যা।

(vii) একটি নির্দিষ্ট বিন্দুকে কেন্দ্র করে একটিই বৃত্ত আঁকা সম্ভব – মিথ্যা।

(viii) দুটি সর্বসম বৃত্তের ব্যাসার্ধের দৈর্ঘ্য সমান – সত্য।

কষে দেখি – 3.2

1. O কেন্দ্রীয় একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি এবং AB একটি জ্যা-এর দৈর্ঘ্য 8 সেমি। O বিন্দু থেকে AB জ্যা-এর দূরত্ব হিসাব করে লিখি।

উত্তর –

O কেন্দ্রীয় বৃত্তের জ্যা AB। O, A যুক্ত করা হলো। OA = 5 সেমি, AB = 8 সেমি
O বিন্দু থেকে OD⟂AB অঙ্কন করা হলো।
∴ O বিন্দু থেকে AB জ্যা-এর দূরত্ব = OD
যেহেতু, O কেন্দ্র থেকে OD, AB জ্যা-এর উপর লম্ব, সুতরাং, D, AB এর মধ্যবিন্দু।

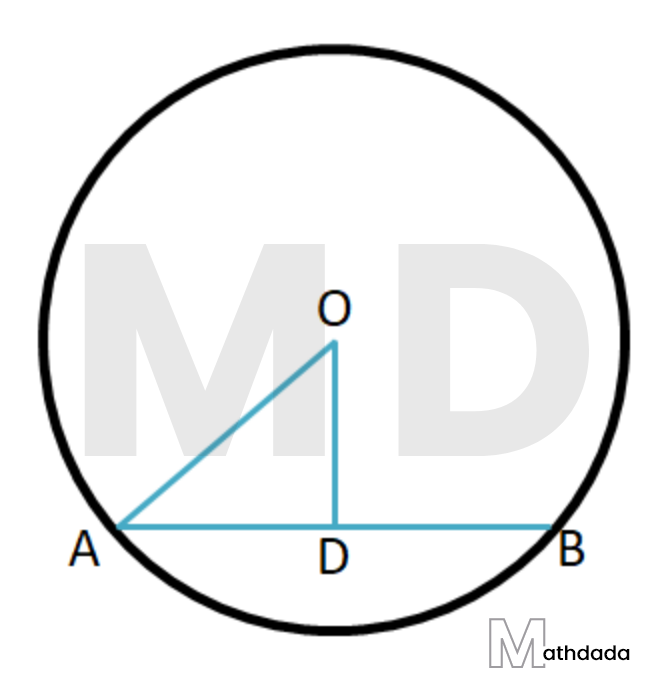
∴ AD = ½ AB = ½ × 8 = 4 সেমি
△OAD একটি সমকোণী ত্রিভুজ।
পিথাগোরাসের উপপাদ্য অনুযায়ী,
OD2 = OA2 – AD2 = (5)2 – (4)2 = 25 – 16 = 9
∴ OD = 3 সেমি ∴ O বিন্দু থেকে AB জ্যা-এর দূরত্ব 3 সেমি।

2. O কেন্দ্রীয় একটি বৃত্তের ব্যাসের দৈর্ঘ্য 26 সেমি। O বিন্দু থেকে PQ জ্যা-এর দূরত্ব 5 সেমি। PQ জ্যা-এর দৈর্ঘ্য হিসাব করে লিখি।

উত্তর –

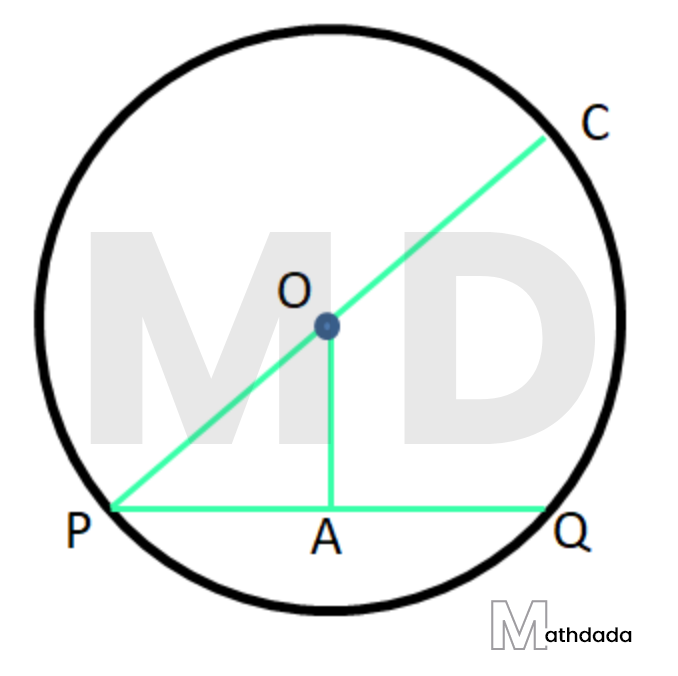
O কেন্দ্রীয় বৃত্তের PQ একটি জ্যা। O থেকে PQ –এর উপর OA লম্ব অঙ্কন করা হল। সুতরাং, O বিন্দু থেকে PQ জ্যা –এর দূরত্ব = OA = 5 সেমি।
O, P বিন্দুদ্বয় যুক্ত করা হল।প্রশ্নানুসারে, বৃত্তটির ব্যাসের দৈর্ঘ্য = 26 সেমি
∴ ব্যাসার্ধ =\frac{26}{2}=13সেমি।
সুতরাং, OP = 13 সেমি এবং OA = 5 সেমি
OPA একটি সমকোণী ত্রিভুজ
∴ পিথাগোরাসের উপপাদ্য অনুসারে A{{P}^{2}}=O{{P}^{2}}-O{{A}^{2}}=\left( {{13}^{2}}-{{5}^{2}} \right)=169-25=144
∴ AP = \sqrt{144}=12 সেমি।
যেহেতু, কেন্দ্র থেকে বৃত্তের জ্যা –এর উপর অঙ্কিত লম্ব জ্যা –কে সমদ্বিখন্ডিত করে
∴ PQ = 2AP = 2 × 12 = 24 সেমি।
সুতরাং, PQ জ্যা –এর দৈর্ঘ্য 24 সেমি।

3. O কেন্দ্রীয় একটি বৃত্তের PQ জ্যা-এর দৈর্ঘ্য 4 সেমি এবং O বিন্দু থেকে PQ-এর দূরত্ব 2.1 সেমি। বৃত্তের ব্যাসের দৈর্ঘ্য হিসাব করে লিখি।

উত্তর –

O কেন্দ্রীয় বৃত্তের PQ জ্যা –এর দৈর্ঘ্য = 4 সেমি
O বিন্দু থেকে OS⟂PQ অঙ্কন করা হল।

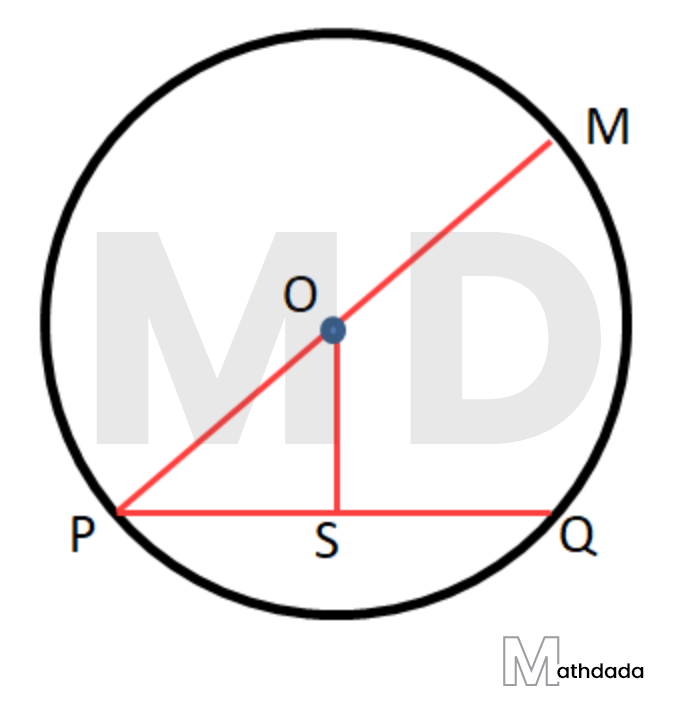
সুতরাং, O বিন্দু থেকে PQ –এর দূরত্ব  = OS = 2.1 সেমি
O, P বিন্দুদ্বয় যুক্ত করা হল।
OP বৃত্তের ব্যাসার্ধ, PS = ½ PQ = ½ × 4 = 2 সেমি।
OPS সমকোণী ত্রিভুজের, পিথাগোরাসের সূত্র অনুসারে O{{P}^{2}}=P{{S}^{2}}+O{{S}^{2}}=\left( {{2}^{2}}+{{2.1}^{2}} \right)=4+4.41=8.41
∴ OP = \sqrt{8.41}=2.9 সেমি
∴ বৃত্তটির ব্যাস = 2 × OP = 2 × 2.9 = 5.8 সেমি।

4. O কেন্দ্রীয় বৃত্তে 6 সেমি ও 8 সেমি দৈর্ঘ্যের দুটি জ্যা। যদি ছোটো দৈর্ঘ্যের জ্যাটির বৃত্তের কেন্দ্র থেকে দূরত্ব 4 সেমি হয়, তাহলে অপর জ্যাটির কেন্দ্র থেকে দূরত্ব কত তা হিসাব করে লিখি।

উত্তর –

O কেন্দ্রীয় বৃত্তের জ্যা AB = 8 সেমি, জ্যা CD = 6 সেমিকেন্দ্র O থেকে জ্যা CD –এর উপর লম্ব OE অঙ্কন করা হল।

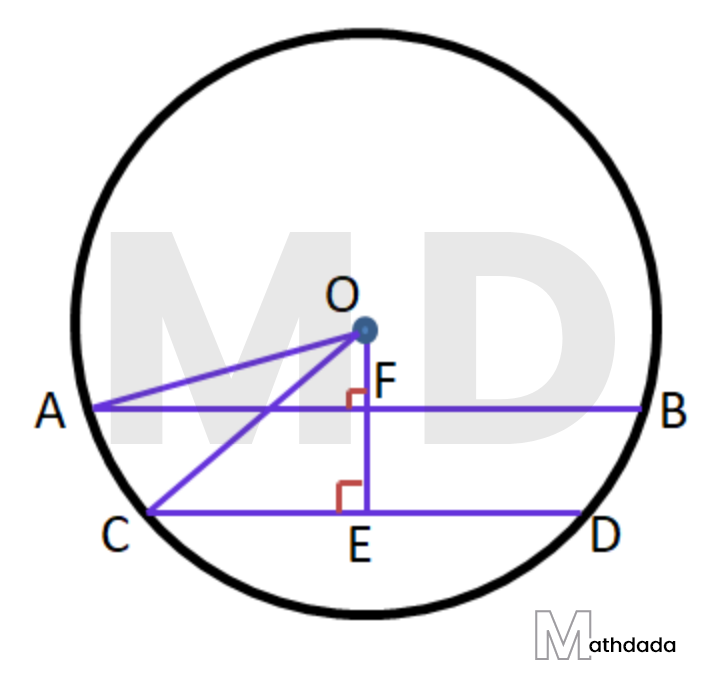
∴ CE = ½ CD = ½ × 6 = 3 সেমি
O, C বিন্দুদ্বয় যুক্ত করা হল।
O বিন্দু থেকে CD –এর দূরত্ব = 4 সেমি
∴ OE = 4 সেমি
OCE সমকোণী ত্রিভুজেO{{C}^{2}}=C{{E}^{2}}+O{{E}^{2}}=\left( {{3}^{2}}+{{4}^{2}} \right)=9+16=25 [ পিথাগোরাসের উপপাদ্য অনুসারে ]
∴ OC = \sqrt{25}=5 সেমি
AB জ্যা –এর A বিন্দু ও বৃত্তের কেন্দ্র O বিন্দুদ্বয় যুক্ত করা হল।
এখন, OA = OC = 5 সেমি [ একই বৃত্তের ব্যাসার্ধ]
O কেন্দ্র থেকে AB জ্যা –এর উপর লম্ব OF অঙ্কন করা হল।
∴ AF = ½ AB = ½ × 8 = 4 সেমি।
OAF সমকোণী ত্রিভুজের O{{F}^{2}}=O{{A}^{2}}-A{{F}^{2}}=\left( {{5}^{2}}-{{4}^{2}} \right)=25-16=9 [ পিথাগোরাসের উপপাদ্য অনুসারে ]
∴ OF = \sqrt{9}=3 সেমি
∴ অপর জ্যাটির কেন্দ্র থেকে দূরত্ব = 3 সেমি।

5. যদি কোনো বৃত্তের একটি জ্যা-এর দৈর্ঘ্য 48 সেমি এবং কেন্দ্র থেকে ওই জ্যা-এর দূরত্ব 7 সেমি হয়, তবে ওই বৃত্তের কেন্দ্র থেকে যে জ্যা-এর দূরত্ব 20 সেমি, সেই জ্যা-এর দৈর্ঘ্য কত হবে তা হিসাব করে লিখি।

উত্তর –

O কেন্দ্রীয় বৃত্তের PQ জ্যা= 48 সেমি
OA⟂PQ অঙ্কন করা হল।

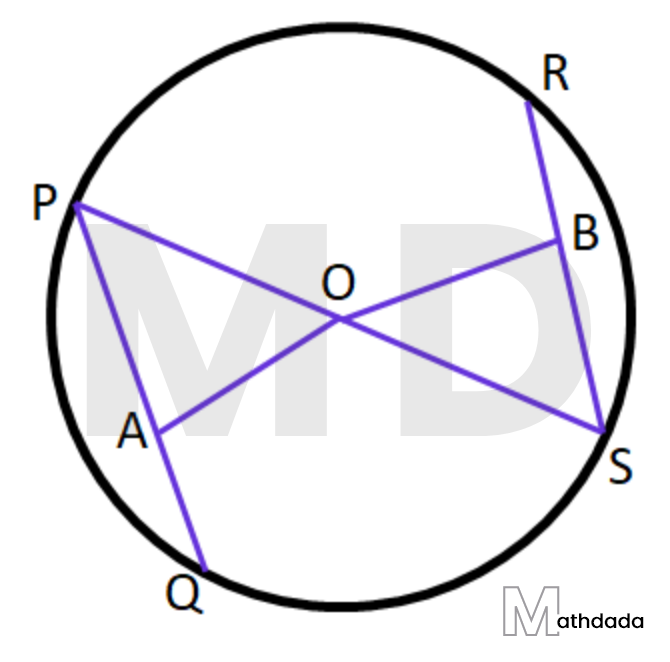
∴ PA = ½ PQ = ½ × 48 =24 সেমি।
প্রশ্নানুসারে, OA = 7 সেমি
O, P বিন্দুদ্বয় যুক্ত করা হল। OP বৃত্তটির ব্যাসার্ধ।
OAP সমকোণী ত্রিভুজে O{{P}^{2}}=O{{A}^{2}}+P{{A}^{2}}=\left( {{7}^{2}}+{{24}^{2}} \right)=49+576=625 [ পিথাগোরাসের উপপাদ্য অনুসারে ]
∴ OP = \sqrt{625}=25 সেমি।
∴ বৃত্তটির ব্যাসার্ধ = 25 সেমি।
এবার, O কেন্দ্র থেকে RS জ্যা –এর দূরত্ব 20 সেমি।
∴ O বিন্দু থেকে অঙ্কিত OB⟂RS –এর দৈর্ঘ্য = 20 সেমি।
∴ OP = OS = 25 সেমি [ একই বৃত্তের ব্যাসার্ধ ]
OSB সমকোণী ত্রিভুজে S{{B}^{2}}=O{{S}^{2}}-O{{B}^{2}}=\left( {{25}^{2}}-{{20}^{2}} \right)=625-400=225 [ পিথাগোরাসের উপপাদ্য অনুসারে ] 
∴ SB = \sqrt{225}=15 সেমি
যেহেতু, OB⟂RS ⇒ RS = 2SB = 2 15 = 30 সেমি।
∴ নির্নেয় জ্যা –এর দৈর্ঘ্য 30 সেমি।

6. পাশের O কেন্দ্রীয় বৃত্তের ছবিতে OP ⟂ AB; AB = 6 সেমি এবং PC = 2 সেমি হলে, বৃত্তের ব্যাসার্ধের দৈর্ঘ্য হিসাব করে লিখি।

উত্তর –

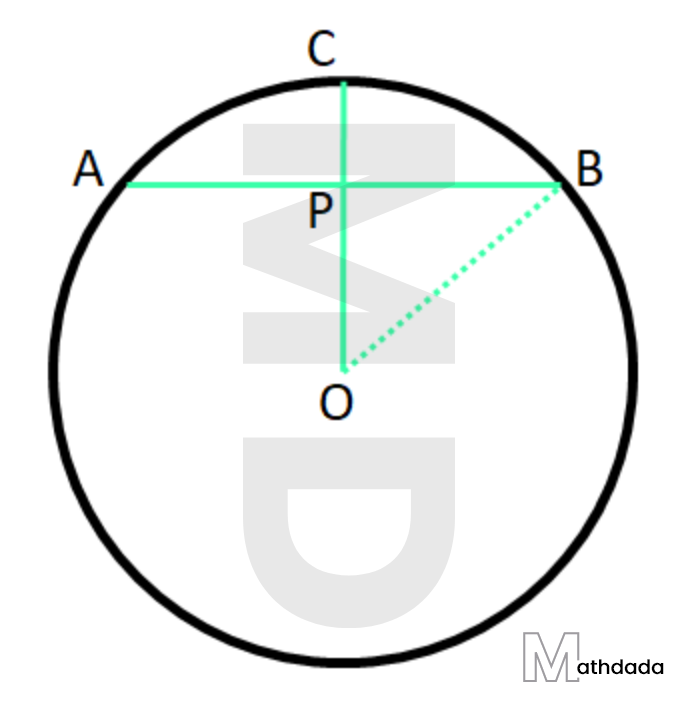
O কেন্দ্রীয় বৃত্তের AB জ্যা = 6 সেমি
OP⟂AB সুতরাং P, AB –এর মধ্যবিন্দু।
OP –কে বৃত্তের পরিধি পর্যন্ত বর্ধিত করায় C বিন্দুতে মিলিত হয়েছে।
প্রশ্নানুসারে, PC = 2 সেমি
মনেকরি বৃত্তটির ব্যাসার্ধ = r সেমি।
OB = OC = r [ একই বৃত্তের ব্যাসার্ধ ]
OP = OC – PC = (r – 2 ) সেমি।
∴ BP = AP = ½ AB = ½ × 6 = 3 সেমি।
OPB সমকোণী ত্রিভুজের\[B{{P}^{2}}=O{{B}^{2}}-O{{P}^{2}}\] \[\Rightarrow {{3}^{2}}={{r}^{2}}-{{\left( r-2 \right)}^{2}}\] \[\Rightarrow 9={{r}^{2}}-\left( {{r}^{2}}-4r+4 \right)\] \[\Rightarrow 9={{r}^{2}}-{{r}^{2}}+4r-4\] \[\Rightarrow 9=4r-4\] \[\Rightarrow 4r=9+4\] \[\therefore \,\,r=\frac{13}{4}=3.25\]
∴ বৃত্তটির ব্যাসার্ধ = 3.25 সেমি।

7. একটি সরলরেখা দুটি এককেন্দ্রীয় বৃত্তের একটিকে A ও B বিন্দুতে এবং অপরটিকে C ও D বিন্দুতে ছেদ করেছে। যুক্তি দিয়ে প্রমাণ করি যে AC = DB

উত্তর –

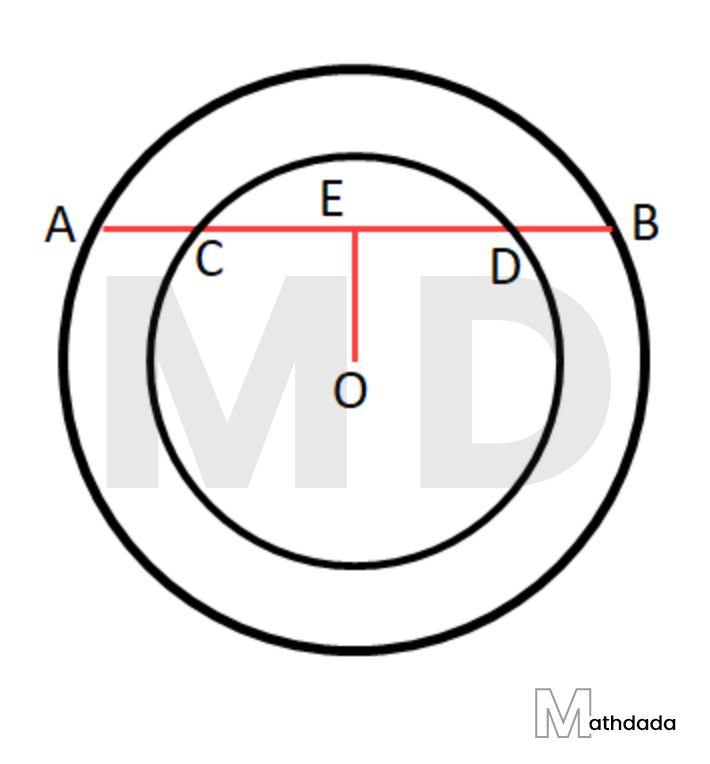
মনেকরি, AB সরলরেখা O কেন্দ্রীয় দুটি বৃত্তকে A ও B এবং C ও D বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে যে, AC = DB
অঙ্কন – O বিন্দু থেকে OE⟂AB অঙ্কন করা হল।
প্রমাণ – E বিন্দু AB –এর মধ্যবিন্দু এবং E বিন্দু CD –এর মধ্যবিন্দু।
সুতরাং, AE  = BE এবং CE = DE
∴ AE – CE = BE – DE
∴ AC = DB (প্রমাণিত)

8. প্রমাণ করি, কোনো বৃত্তের দুটি পরস্পরছেদি জ্যা পরস্পরকে সমদ্বিখন্ডিত করতে পারে না, যদি না উভয়েই বৃত্তের ব্যাস হয়।

উত্তর –

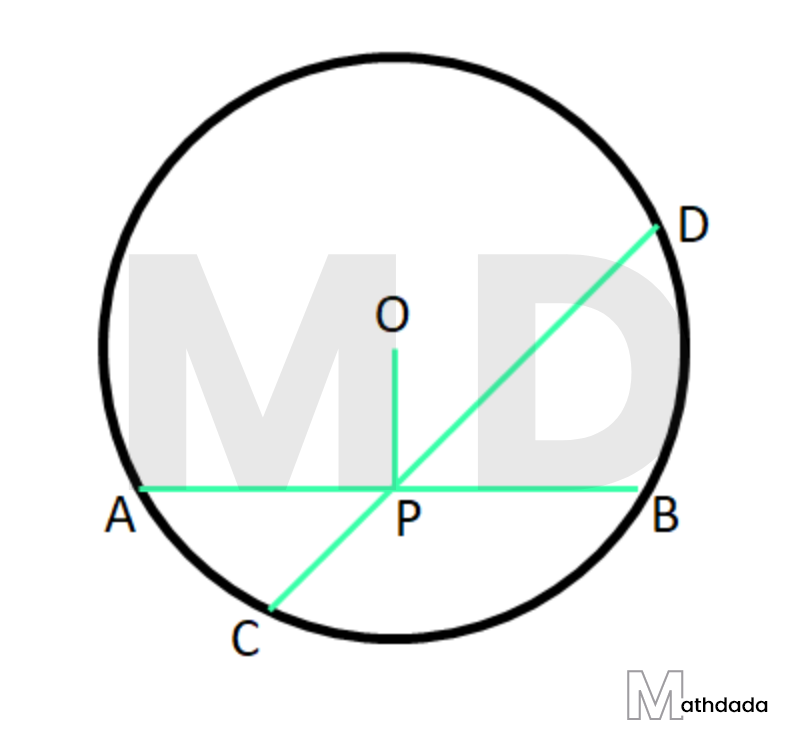
মনেকরি, O কেন্দ্রীয় একটি বৃত্তের AB ও CD দুটি জ্যা পরস্পরকে P বিন্দুতে এমনভাবে ছেদ করেছে যে, P বিন্দু AB –এর মধ্যবিন্দু।
প্রমাণ করতে হবে যে, P, CD –এর মধ্যবিন্দু হবে না।
অঙ্কন – O, P যুক্ত করা হল।
প্রমাণ – P, AB –এর মধ্যবিন্দু।
∴ OP⟂ABযেহেতু, AB ও CD উভয়েই P বিন্দুগামী
∴ AB ও CD উভয়েই OP –এর উপর P বিন্দুতে লম্ব হতে পারে না।
যেহেতু, AB, OP –এর উপর লম্ব।
∴ CD, OP –এর উপর লম্ব নয়।
আবার, যেহেতু কোনো জ্যা –এর মধ্যবিন্দু ও বৃত্তের কেন্দ্র সংযোজক রেখাংশ জ্যা –এর উপর লম্ব।
সুতরাং, P, CD –এর মধ্যবিন্দু নয়। [ প্রমাণিত]

9. X ও Y কেন্দ্রবিশিষ্ট দুটি বৃত্ত পরস্পরকে A ও B বিন্দুতে ছেদ করেছে। XY-এর মধ্যবিন্দু S-এর সংগে A বিন্দু যুক্ত করলাম এবং A বিন্দু দিয়ে SA-এর উপর লম্ব অঙ্কন করলাম যা বৃত্ত দুটিকে P ও Q বিন্দুতে ছেদ করল। প্রমাণ করি যে, PA = AQ.

উত্তর –

দেওয়া আছে যে, X ও Y কেন্দ্রবিশিষ্ট দুটি বৃত্ত পরস্পরকে A ও B বিন্দুতে ছেদ করেছে। XY –এর মধ্যবিন্দু S। S, A বিন্দুদ্বয় যুক্ত করা হল। A বিন্দু দিয়ে SA –এর উপর লম্ব PAQ অঙ্কন করা হল। PAQ বৃত্তদ্বয়কে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে যে, PA = AQ
অঙ্কন – XC⟂PA এবং YD⟂AQ অঙ্কন করা হল। সুতরাং, C ও D যথাক্রমে PA ও AQ –এর মধ্যবিন্দু। XY ও XD যুক্ত করা হল। XD যেন AS –কে G বিন্দুতে ছেদ করে।

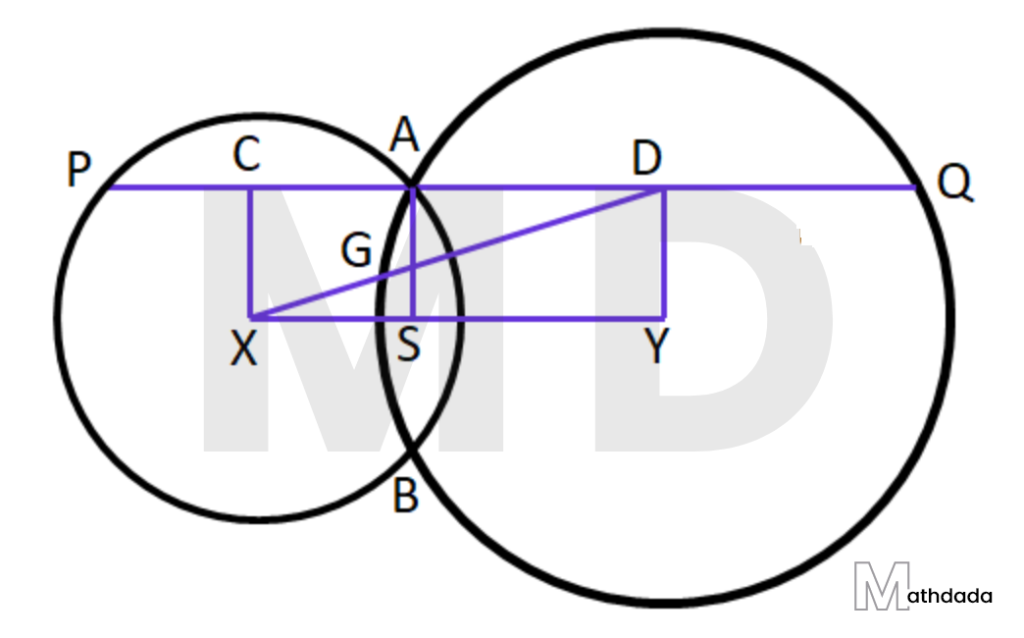
প্রমাণ – XC, SA এবং YD প্রত্যেকেই PQ –এর উপর লম্ব।
∴ XC||SA||YD
△XYD –এর XY –এর মধ্যবিন্দু S এবং SG||DY [ যেহেতু, SA||YD]
∴ G, XD –এর মধ্যবিন্দু
আবার, △DCX –এর G, XD –এর মধ্যবিন্দু। EA||XC [ যেহেতু, XC||XA]
∴ A বিন্দু CD –এর মধ্যবিন্দু
∴ CA = ½ CD এবং DA = ½ CD
∴ CA = DA
আবার, যেহেতু XC⟂AP
∴ C, AP –এর মধ্যবিন্দু
অর্থাৎ, CA = ½ PA এবং YD⟂AQ
∴ D, AQ –এর মধ্যবিন্দু
অর্থাৎ, DA = ½ AQ
যেহেতু CA = DA
∴ ½ PA = ½ AQ
সুতরাং, PA = AQ [ প্রমাণিত]

10. O কেন্দ্রীয় বৃত্তের 10 সেমি ও 24 সেমি দৈর্ঘ্যের দুটি সমান্তরাল জ্যা AB এবং CD কেন্দ্রের বিপরীত পার্শ্বে অবস্থিত। যদি AB ও CD-জ্যা দুটির মধ্যে দূরত্ব 17 সেমি হয়, তবে হিসাব করে বৃত্তের ব্যাসার্ধের দৈর্ঘ্য লিখি।

উত্তর সংকেত – ধরি, বৃত্তের দৈর্ঘ্য r সেমি এবং বৃত্তের কেন্দ্র থেকে AB জ্যা-এর দূরত্ব x সেমি। ∴ বৃত্তের কেন্দ্র থেকে CD জ্যা-এর দূরত্ব (17 – x) সেমি। ∴ r2 = x2 + 52 এবং r2 = (17 – x)2 + (12)2 , সুতরাং, x2 + 52 = (17 – x)2 + 122 ∴x = 12

উত্তর –

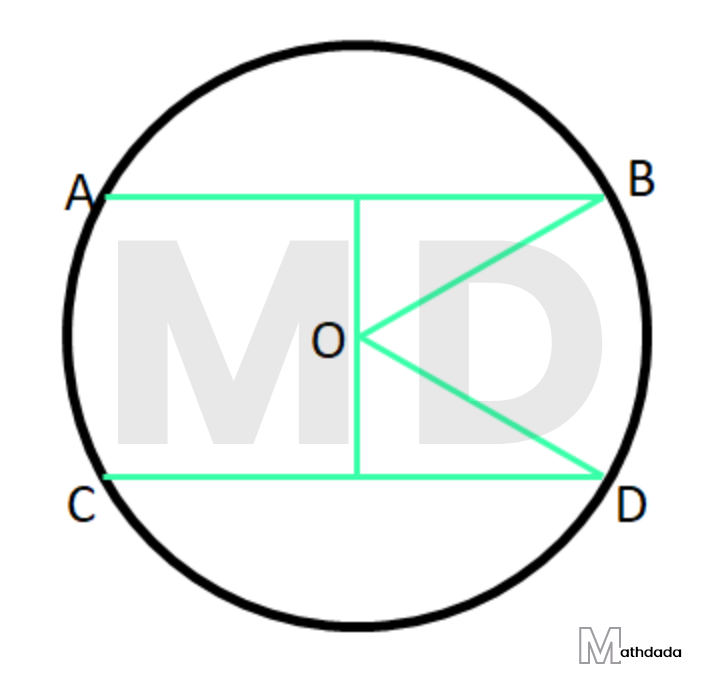
ধরি, বৃত্তের দৈর্ঘ্য r সেমি এবং বৃত্তের কেন্দ্র থেকে AB জ্যা-এর দূরত্ব x সেমি।
∴ বৃত্তের কেন্দ্র থেকে CD জ্যা-এর দূরত্ব (17 – x) সেমি।
∴ r² = x² + 5² এবং r² = (17 – x)² + (12)² ,
সুতরাং, x² + 5² = (17 – x)² + 12²
∴ x = 12
r² = x² + 5² –এ x = 12 বসিয়ে পাই,
\[{{r}^{2}}={{12}^{2}}+{{5}^{2}}=169\]\[\therefore \,\,r=\sqrt{169}=13\]
সুতরাং, বৃত্তটির ব্যাসার্ধের দৈর্ঘ্য = 13 সেমি।

11. দুটি বৃত্তের কেন্দ্র P এবং Q; বৃত্ত দুটি  A এবং B বিন্দুতে ছেদ করে। A বিন্দু দিয়ে PQ সরলরেখাংশের সমান্তরাল সরলরেখা বৃত্ত দুটিকে C ও D বিন্দুতে ছেদ করে। প্রমাণ করি যে, CD = 2PQ

উত্তর –

দেওয়া আছে যে, দুটি বৃত্তের কেন্দ্র P এবং Q; বৃত্ত দুটি  A এবং B বিন্দুতে ছেদ করে। A বিন্দু দিয়ে PQ সরলরেখাংশের সমান্তরাল সরলরেখা বৃত্ত দুটিকে C ও D বিন্দুতে ছেদ করে।
প্রমাণ করতে হবে যে, CD = 2PQ
অঙ্কন – PR⟂CA এবং SQ⟂AD অঙ্কন করা হল। সুতরাং, R ও S যথাক্রমে CA ও AD –এর মধ্যবিন্দু।
[9 নং প্রশ্নের সমাধান থেকে পাই, CA = AD এবং CD||PQ]

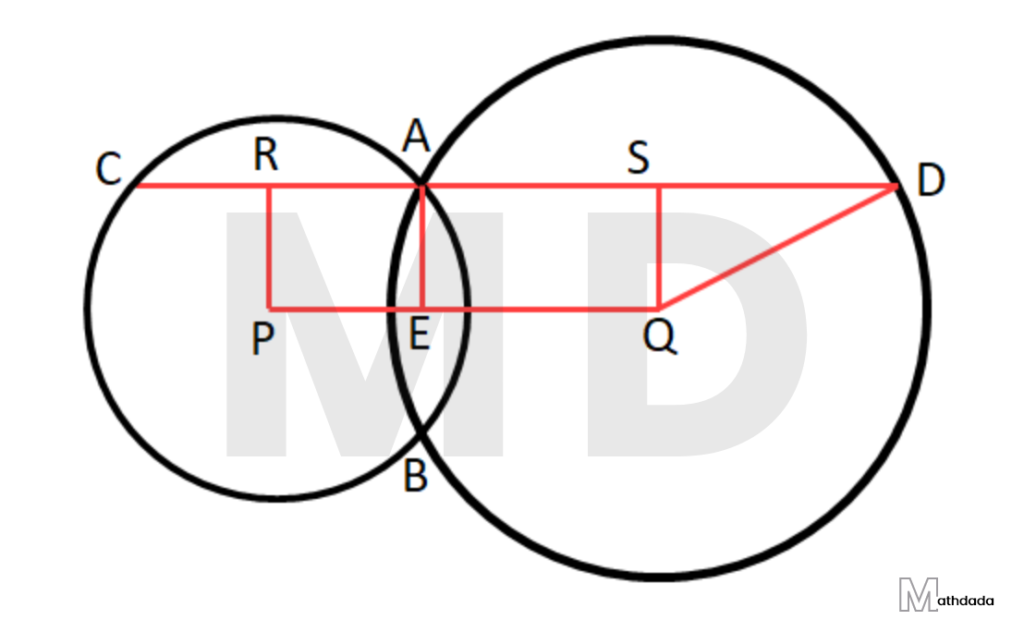
প্রমাণ – RP, AE ও SQ প্রত্যেকে PQ –এর উপর লম্ব।
∴RP||AE||SQ
R বিন্দু AC এবং S বিন্দু AD –এর মধ্যবিন্দু।
∴CR = RA এবং AS = AD
∴RS = PQ [ যেহেতু, RS||PQ RP||SQ]
CR = RA = AS = SD
RS = PQ
∴ CD = CR + RA + AS + SD
বা, CD = CR + PQ + SD
বা, CD = PQ + PQ
∴ CD = 2PQ [ প্রমাণিত ]

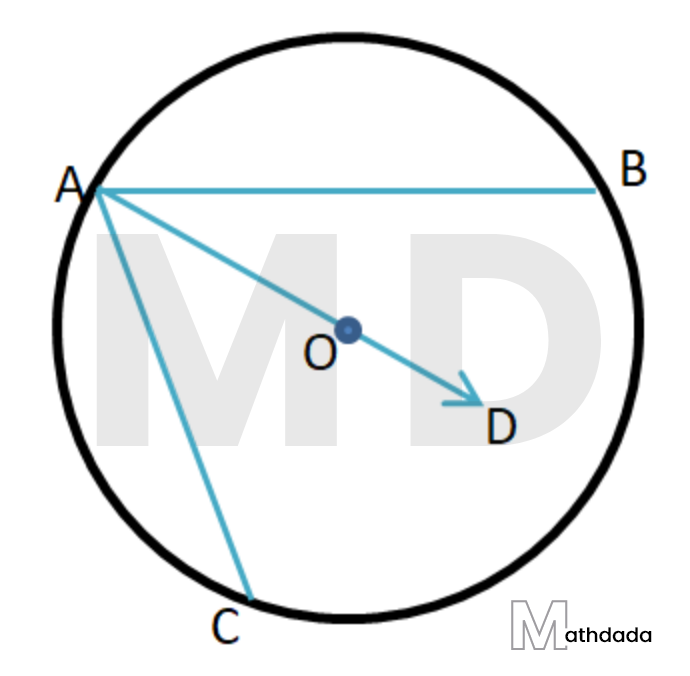
12. একটি বৃত্তের AB ও AC জ্যা দুটি সমান। প্রমাণ করি যে, ∠BAC-এর সমদ্বিখণ্ডক কেন্দ্রগামী।

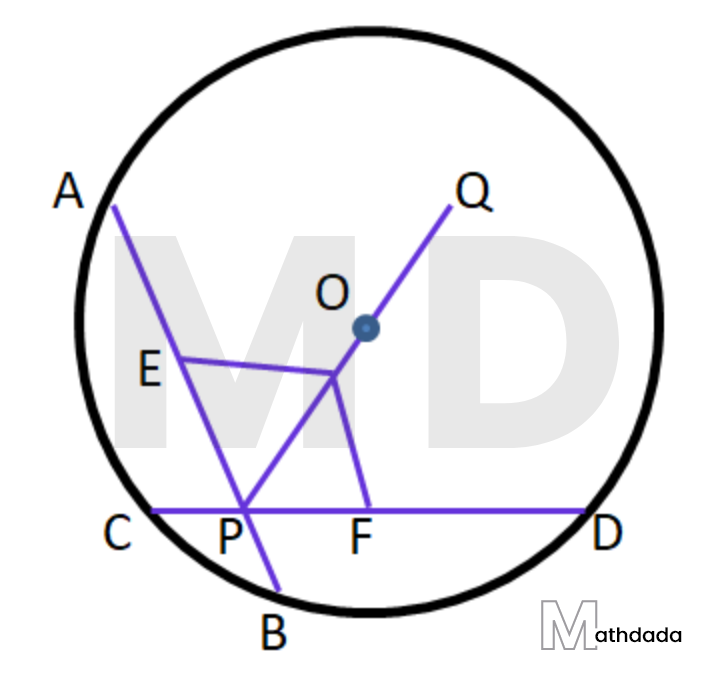
13. একটি বৃত্তের দুটি পরস্পরচ্ছেদী জ্যা-এর অন্তর্ভুত কোণের সমদ্বিখণ্ডক যদি কেন্দ্রগামী হয়, তাহলে প্রমাণ করি যে জ্যা দুটি সমান।

14. প্রমাণ করি, একটি বৃত্তের দুটি জ্যা-এর মধ্যে যে জ্যাটি কেন্দ্রের নিকটবর্তী সেটির দৈর্ঘ্য অপর জ্যা-টির দৈর্ঘ্য অপেক্ষা বৃহত্তর।

উত্তর –

দেওয়া আছে যে, O কেন্দ্রস্থ বৃত্তের AB ও CD দুটি জ্যা। এর মধ্যে AB জ্যা, CD  জ্যা অপেক্ষা O কেন্দ্রের নিকটবর্তী।
প্রমাণ করতে হবে যে, AB জ্যা –এর দৈর্ঘ্য, CD জ্যা অপেক্ষা বৃহত্তর অর্থাৎ, AB > CD
অঙ্কন – O, A বিন্দুদ্বয় এবং O, C বিন্দুদ্বয় যুক্ত করা হল।

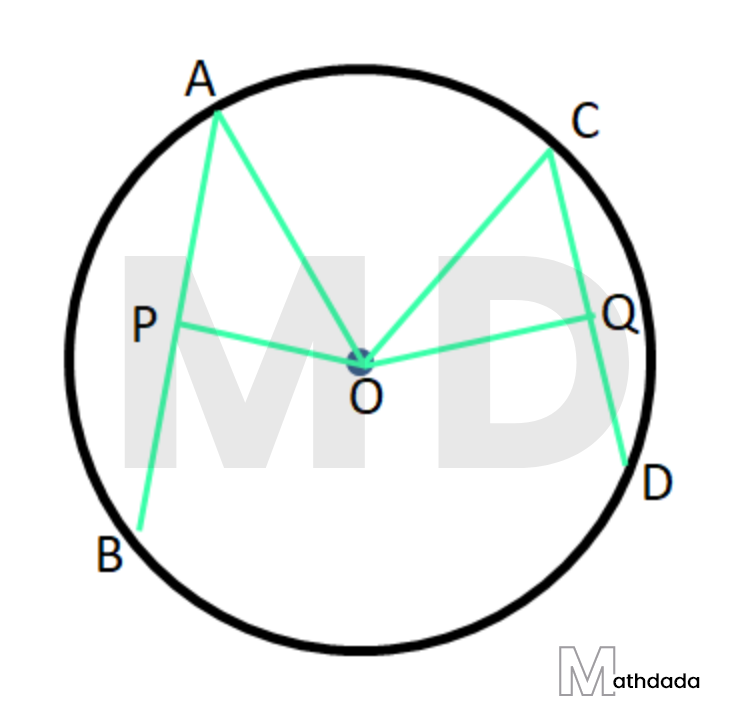
প্রমাণ – যেহেতু OP⟂AB
∴ AP = ½AB এবং APO সমকোণী ত্রিভুজ।
আবার, যেহেতু OQ⟂CD
∴ CQ = ½ CD এবং CQO সমকোণী ত্রিভুজ।
পিথাগোরাসের উপপাদ্য অনুসারে,
AP² + OP² = OA² এবং CQ² + OQ² = OC²
আবার, OA = OC [ একই বৃত্তের ব্যাসার্ধ ]
∴ AP² + OP² = CQ² + OQ²
বা, AP² – CQ² = OQ² – OP² ………(1)
এখন যেহেতু OP < OQ [ প্রশ্নানুসারে ]
∴ OQ > OP
∴ OQ² > OP²
বা, OQ² – OP² > 0
(1) নং থেকে পাই,AP² – CQ² > 0
বা, AP² > CQ²
বা, AP > CQ
বা, ½ AB > ½ CD
∴ AB >  CD [ প্রমাণিত ]

15. একটি বৃত্তের ভিতর যে-কোনো বিন্দু দিয়ে ক্ষুদ্রতম জ্যা কোনটি হবে তা প্রমাণ করে লিখি।

16. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

(A) বহুবিকল্পীয় প্রশ্ন(M.C.Q)

(i) O কেদন্রীয় বৃত্তের AB ও CD জ্যা দুটির দৈর্ঘ্য সমান। ∠AOB = 60° হলে, ∠COD-এর মান
(a) 40° (b) 30° (c) 60° (d) 90°

উত্তর –

যেহেতু, AB = CD
OA = OB = OC = OD [ একই বৃত্তের ব্যাসার্ধ ]
∴ △AOB ≅ △COD [ S-S-S সর্বসমতার শর্তানুসারে ]
∴ ∠AOB = ∠COD = 60°
∴ নির্নেয় উত্তর হল – (c) 60°

(ii) একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 13 সেমি এবং বৃত্তের একটি জ্যা-এর দৈর্ঘ্য 10 সেমি। বৃত্তের কেন্দ্র থেকে জ্যা-এর দূরত্ব
(a) 12.5 সেমি (b) 12 সেমি (c) √69 সেমি (d) 24 সেমি

উত্তর –

জ্যা AB = 10 সেমি, ব্যাসার্ধ OA = 13 সেমি এবং OC⟂AB
∴ AC = ½ AB = ½ × 10 = 5 সেমি
∴ OC² = OA² – AC² = 13² – 5² = 144
∴ OC = \sqrt{144}=12সেমি
∴ নির্নেয় উত্তর হল – (b) 12 সেমি

(iii) O কেন্দ্রীয় বৃত্তের AB ও CD দুটি সমান দৈর্ঘ্যের জ্যা। O বিন্দু থেকে AB জ্যা-এর দূরত্ব 4 সেমি হলে, CD জ্যা-এর দূরত্ব
(a) 2 সেমি (b) 4 সেমি (c) 6 সেমি (d) 8 সেমি

উত্তর –

AB =   CD, OP = 4 সেমি
কেন্দ্র থেকে CD জ্যা –এর দূরত্ব OQ
△AOP ≅ △COQ
∴ OP = OQ = 4 সেমি
∴ নির্নেয় উত্তর হল – (b) 4 সেমি

(iv) AB ও CD দুটি সমান্তরাল জ্যা-এর প্রত্যেকটির দৈর্ঘ্য 16 সেমি। বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 10 সেমি হলে, জ্যা দুটির মধ্যে দূরত্ব
(a) 12 সেমি (b) 16 সেমি (c) 20 সেমি (d) 5 সেমি

উত্তর –

AB||CD, AB = CD = 16 সেমি
OB = OD = 10 সেমি
OP⟂AB সুতরাং, BP = ½ AB = 8 সেমি
OQ⟂CD সুতরাং, QD = ½ CD = 8 সেমি
△OPB –এর
OP² = OB² – BP² = 10² – 8² = 36
∴ OP = \sqrt{36}=6 সেমি
△OQD –এর
OQ² = OD² – QD² = 10² – 8² = 36
∴ OQ = \sqrt{36}=6 সেমি
∴ PQ = OP + OQ = 6 + 6 = 12 সেমি
∴ নির্নেয় উত্তর হল – (a) 12 সেমি

(v) দুটি সমকেন্দ্রীয় বৃত্তের কেন্দ্র O; একটি সরলরেখা একটি বৃত্তকে A ও B বিন্দুতে এবং অপর বৃত্তকে C ও D বিন্দুতে ছেদ করে। AC = 5 সেমি হলে BD-এর দৈর্ঘ্য
(a) 2.5 সেমি (b) 5 সেমি (c) 10 সেমি (d) কোনটিই নয়।

উত্তর –

OP⟂CD অর্থাৎ, OP⟂AB
AP = PB এবং CP = PD
∴ CP – AP = PD – PB
বা, AC = BD = 5
∴ নির্নেয় উত্তর হল – (b) 5 সেমি

(B) সত্য / মিথ্যা লিখি –

(i) তিনটি সমরেখ বিন্দু দিয়ে যায় এরকম একটি বৃত্ত অঙ্কন করা যায়।

উত্তর – সত্য।

(ii) ABCDA ও ABCEA বৃত্ত দুটি একই বৃত্ত।

উত্তর – সত্য।

(iii) O কেন্দ্রীয় বৃত্তের AB এবং AC জ্যা দুটি OA ব্যাসার্ধের বিপরীত পার্শ্বে অবস্থিত হলে, ∠OAB = ∠OAC

উত্তর – মিথ্যা।

(C) শূন্যস্থান পূরণ করি –

(i) O কেন্দ্রীয় বৃত্তের PQ ও RS জ্যা দুটির দৈর্ঘ্যের অনুপাত 1:1 হলে, ∠POQ: ∠ROS = _____

উত্তর – ∠POQ: ∠ROS = 1 : 1

(ii) বৃত্তের কোনো জ্যা-এর লম্বসমদ্বিখন্ডক ওই বৃত্তের _____।

উত্তর – কেন্দ্রগামী।

17.(i) 10 সেমি দৈর্ঘ্যের ব্যাসার্ধের দুটি সমান বৃত্ত পরস্পরকে ছেদ করে এবং তাদের সাধারণ জ্যা-এর দৈর্ঘ্য 12 সেমি। বৃত্ত দুটির কেন্দ্রদ্বয়ের মধ্যে দূরত্ব নির্ণয় করি।

উত্তর –

দেওয়া আছে যে, A কেন্দ্রীয় ও B কেন্দ্রীয় বৃত্তদ্বয়ের ব্যাসার্ধ 10 সেমি।
∴ AC = BC = 10 সেমি
বৃত্তদ্বয়ের সাধারণ জ্যা = CD = 12 সেমি।
যেহেতু, OC⟂AB সুতরাং, OC = ½ CD = ½ × 12 = 6 সেমি
সমকোণী ত্রিভুজ AOC থেকে পাই,
AO² = AC² – OC² = 10² – 6² = 64
∴ AO = \sqrt{64}=8 সেমি
সমকোণী ত্রিভুজ BOC থেকে পাই,
OB² = BC² – OC² = 10² – 6² = 64
∴ OB = \sqrt{64}=8সেমি
∴ AB = AO + OB = 8 + 8 = 16সেমি
∴ বৃত্ত দুটির কেন্দ্রদ্বয়ের মধ্যে দূরত্ব 16 সেমি।

(ii) 5 সেমি দৈর্ঘ্যের ব্যাসার্ধের একটি বৃত্তে AB এবং AC দুটি সমান দৈর্ঘ্যের জ্যা। বৃত্তের কেন্দ্র ABC ত্রিভুজের বাইরে অবস্থিত। AB = AC = 6 সেমি হলে, BC জ্যা-এর দৈর্ঘ্য নির্ণয় করি।

উত্তর –

(iii) O কেন্দ্রীয় বৃত্তে AB ও CD জ্যা দুটির দৈর্ঘ্য সমান। ∠AOB = 60° এবং CD = 6 সেমি হলে, বৃত্তের ব্যাসার্ধের দৈর্ঘ্য কত তা নির্ণয় করি।

উত্তর –

দেওয়া আছে যে, AB = CD = 6 সেমি
OA = OB [ একই বৃত্তের ব্যাসার্ধ ]
∠AOB = 60°
△ABO –এর
∠A = ∠B [ কারণ OA = OB সমান সমান বাহুর বিপরীত কোনগুলি সমান ]
∴ ∠A + ∠B = 180° – 60° = 120°
∴ ∠A = 60°, ∠B = 60°
অর্থাৎ, ∠A = ∠B = ∠O = 60°
OA = OB = AB = 6 সেমি [ যেহেতু, ত্রিভুজের তিনটি কোণের মান সমান হলে ত্রিভুজটি সমবাহু ত্রিভুজ হয়।]
∴ বৃত্তের ব্যাসার্ধের দৈর্ঘ্য = 6 সেমি

(iv) O কেন্দ্রীয় বৃত্তের ভিতর P যে-কোনো একটি বিন্দু। বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি এবং OP = 3 সেমি হলে, P বিন্দুগামী যে জ্যাটির দৈর্ঘ্য নূন্যতম তা নির্ণয় করি।

উত্তর –

(v) P ও Q কেন্দ্রবিশিষ্ট দুটি বৃত্ত A ও B বিন্দুতে ছেদ করে। A বিন্দু দিয়ে PQ-এর সমান্তরাল সরলরেখা বৃত্তদুটিকে যথাক্রমে C ও D বিন্দুতে ছেদ করে। PQ = 5 সেমি হলে CD-এর দৈর্ঘ্য কত তা নির্ণয় করি।

দেওয়া আছে যে, P ও Q কেন্দ্রবিশিষ্ট দুই বৃত্ত A ও B বিন্দুতে ছেদ করেছে। A বিন্দু দিয়ে PQ –এর সমান্তরাল বৃত্ত দুটিকে যথাক্রমে C ও D বিন্দুতে ছেদ করেছে।
∴ CD = 2 × PQ = 2 × 5 = 10 সেমি

;