অষ্টম শ্রেণি – প্রথম অধ্যায় : পুর্বপাঠের পুনরালোচনা সম্পূর্ণ সমাধান

কষে দেখি – 1.1

1. নীচের ছক কাগজে ছবি দেখি ও ছবিগুলি কতটা জায়গা জুড়ে আছে লিখি –

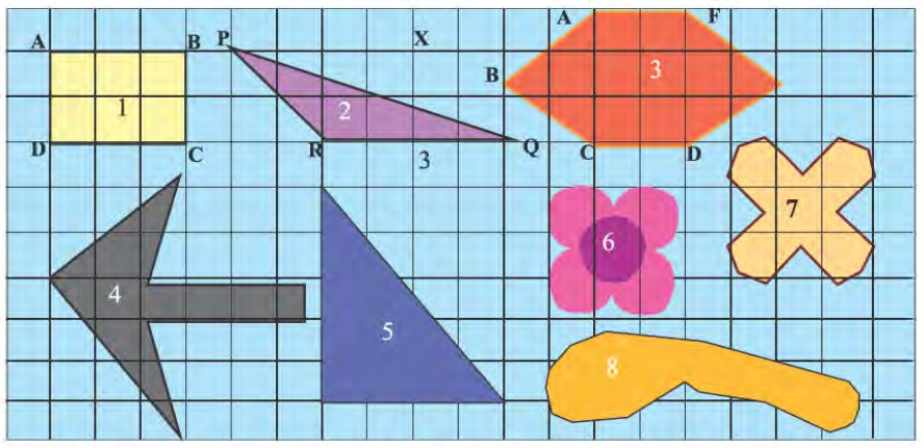
উত্তর –

আকার	অধিকৃত সম্পূর্ণ ক্ষুদ্রতম বর্গক্ষেত্রাকার ঘরের সংখ্যা	অধিকৃত অর্ধেক ক্ষুদ্রতম বর্গক্ষেত্রাকার ঘরের সংখ্যা	অধিকৃত অর্ধেকের বেশি ক্ষুদ্রতম বর্গক্ষেত্রাকার ঘরের সংখ্যা	অধিকৃত অর্ধেকের কম ক্ষুদ্রতম বর্গক্ষেত্রাকার ঘরের সংখ্যা	মোট ক্ষেত্রফল (1টি ক্ষুদ্রতম বর্গক্ষেত্রাকার ঘরের ক্ষেত্রফল = 1 বর্গসেমি)
1	6	–	–	–	6 বর্গসেমি
2	1	–	3	3	4 বর্গসেমি
3	8	2	4	3	12 বর্গসেমি
4	1	–	8	8	9 বর্গসেমি
5	6	–	4	4	10 বর্গসেমি
6	1	–	8	–	7 বর্গসেমি
7	1	–	4	4	5 বর্গসেমি
8	1	–	8	7	9 বর্গসেমি

2. আমিনাদের বাড়ির আয়তক্ষেত্রাকার উঠানের দৈর্ঘ্য 6 মিটার এবং প্রস্থ 4.2 মিটার। ওই উঠানের মাঝখানে  3.5 মিটার × 2.5 মিটার মাপের একটি আয়তক্ষেত্রাকার শতরঞ্চি পাতলাম। শতরঞ্চি বাদে বাকি উঠানের ক্ষেত্রফল হিসাব করে লিখি।

উত্তর –
আমিনাদের বাড়ির আয়তক্ষেত্রাকার উঠানের ক্ষেত্রফল = (6 × 4.2) বর্গমিটার= 25.2 বর্গমিটার
শতরঞ্চির ক্ষেত্রফল = (3.5 × 2.5) বর্গমিটার = 8.75 বর্গমিটার
∴ শতরঞ্চি বাদে বাকি উঠানের ক্ষেত্রফল = (25.2 – 8.75) = 16.45

3. অজন্তা হাউসিং কমপ্লেক্সের বর্গক্ষেত্রাকার পার্কের বাইরের চারদিকে 3 মিটার চওড়া একটি রাস্তা আছে। রাস্তা সমেত পার্কের পরিসীমা 484 মিটার হলে রাস্তাটির ক্ষেত্রফল হিসাব করি।

উত্তর –
রাস্তা সমেত বর্গাকার পার্কের পরিসীমা = 484 মিটার
∴ রাস্তা সমেত পার্কের প্রতিটি বাহুর দৈর্ঘ্য = \frac{484}{4}=121মিটার
∴ রাস্তা সমেত পার্কের ক্ষেত্রফল = (121 × 121) বর্গমিটার = 14641 বর্গমিটার
∴ রাস্তা বাদে পার্কের প্রতিটি বাহুর দৈর্ঘ্য = (121 – 2 × 3) মিটার = 115 মিটার
∴ রাস্তা বাদে পার্কের ক্ষেত্রফল = (115 × 115) বর্গমিটার = 13225 বর্গমিটার

∴ রাস্তাটির ক্ষেত্রফল = (14641 – 13225) বর্গমিটার = 1416 বর্গমিটার

4. মিহিরদের আয়তক্ষেত্রাকার বাগানের দৈর্ঘ্য 50 মিটার এবং প্রস্থ 30 মিটার। ওই বাগানের মাঝবরাবর দৈর্ঘ্যের সমান্তরাল 4 মিটার চওড়া একটি রাস্তা বাগানটিকে দুটি সমান ক্ষেত্রফল বিশিষ্ট আয়তক্ষেত্রাকার খন্ডে ভাগ করেছে। রাস্তাটির ক্ষেত্রফল নিজে এঁকে হিসাব করে লিখি।

(a) যদি 4 মিটার চওড়া রাস্তাটি বাগানের মাঝবরাবর প্রস্থের সমান্তরালে হতো এবং বাগানটিকে দুটি সমান খন্ডে ভাগ করত তবে রাস্তাটির ক্ষেত্রফল কী হতো তা নিজে এঁকে হিসাব করে লিখি।

(b) যদি মিহিরদের বাগানের মাঝবরাবর দৈর্ঘ্য ও প্রস্থের সমান্তরাল দুটি রাস্তা থাকত এবং মিহিরদের বাগানকে 4 টি সমান খন্ডে ভাগ করত তখন রাস্তার ক্ষেত্রফল কী হতো তা নিজে এঁকে হিসাব করে লিখি।

উত্তর –
রাস্তাসহ সম্পূর্ণ বাগানের ক্ষেত্রফল = (50 × 30)বর্গমিটার = 1500 বর্গমিটার
ওই বাগানের মাঝবরাবর দৈর্ঘ্যের সমান্তরাল 4 মিটার চওড়া একটি রাস্তা বাগানটিকে দুটি সমান ক্ষেত্রফল বিশিষ্ট আয়তক্ষেত্রাকার খন্ডে ভাগ করেছে।
∴ রাস্তার দৈর্ঘ্য = 50 মিটার এবং প্রস্থ = 4 মিটার
∴ রাস্তাটির ক্ষেত্রফল = (50 × 4)বর্গমিটার = 200 বর্গমিটার

(a) যদি 4 মিটার চওড়া রাস্তাটি বাগানের মাঝবরাবর প্রস্থের সমান্তরালে হতো এবং বাগানটিকে দুটি সমান খন্ডে ভাগ করত তবে,
∴ রাস্তার দৈর্ঘ্য = 30 মিটার এবং প্রস্থ = 4 মিটার
∴ রাস্তাটির ক্ষেত্রফল = (30 × 4)বর্গমিটার = 120 বর্গমিটার

(b) যদি মিহিরদের বাগানের মাঝবরাবর দৈর্ঘ্য ও প্রস্থের সমান্তরাল দুটি রাস্তা থাকত এবং মিহিরদের বাগানকে 4 টি সমান খন্ডে ভাগ করত তখন,
বাগানের প্রস্থের সমান্তরাল রাস্তাটির দৈর্ঘ্য = 30 মিটার এবং প্রস্থ = 4 মিটার
∴ প্রস্থের সমান্তরাল রাস্তাটির ক্ষেত্রফল = (30 × 4)বর্গমিটার = 120 বর্গমিটার
বাগানের দৈর্ঘ্যের সমান্তরাল রাস্তাটির দৈর্ঘ্য = 50 মিটার এবং প্রস্থ = 4 মিটার
∴ দৈর্ঘ্যের সমান্তরাল রাস্তাটির ক্ষেত্রফল = (50 × 4)বর্গমিটার = 200 বর্গমিটার
বাগানের মধ্যিখানে রাস্তা দুটি পরস্পরকে অতিক্রম করেছে। অর্থাৎ, (4× 4)বর্গমিটার = 16 বর্গমিটার দুবার হিসাব করা হয়েছে।
∴ রাস্তাটির ক্ষেত্রফল = (120 + 200 – 16)বর্গমিটার = 304 বর্গমিটার

5. আমাদের বাড়ির পাশে পাপিয়াদের আয়তক্ষেত্রাকার জমি আছে। এই আয়তক্ষেত্রাকার জমির দৈর্ঘ্য 48 মিটার এবং প্রস্থ 26 মিটার। পাপিয়ারা তাদের জমির চারদিকে 4 মিটার ছেড়ে বাড়ি তৈরি করবে। হিসাব করে দেখি পাপিয়ারা কত বর্গমিটারে তাদের বাড়ি তৈরি করবে।

উত্তর –
আয়তক্ষেত্রাকার জমির ক্ষেত্রফল = (48 × 26)বর্গমিটার = 1268
বর্গমিটার বাড়ির দৈর্ঘ্য = (48 – 2 × 4) মিটার = 40মিটার
এবং প্রস্থ = (26 – 2 × 4) মিটার = 18 মিটার
∴ বাড়ির ক্ষেত্রফল = (40 × 18)বর্গমিটার = 720 বর্গমিটার

6. আমার ভাই দীপু একটি আয়তক্ষেত্রাকার কাগজের পুরোটায় ছবি এঁকেছে যার দৈর্ঘ্য 15 সেমি এবং প্রস্থ 8 সেমি।

(a) যদি দীপু আয়তক্ষেত্রাকার কাগজের প্রস্থ একই রেখে দৈর্ঘ্য দ্বিগুন করত তবে তার ছবির কাগজের ক্ষেত্রফলের কী পরিবর্তন হতো হিসাব করে লিখি।

(b) যদি দীপু তার ছবির কাগজের দৈর্ঘ্য একই রেখে প্রস্থ দ্বিগুন করত তখন তার ছবির কাগজের ক্ষেত্রফলের কী পরিবর্তন হতো হিসাব করি।

(c) যদি দীপু তার ছবির কাগজের দৈর্ঘ্য ও প্রস্থ উভয়কেই দ্বিগুন করত তখন তার ছবির কাগজের খেতফল (a) নং ছবির কাগজের খেত্রফলের কতগুণ হতে পারে হিসাব করি।

(d) কিন্তু দীপু যদি তার কাগজের দৈর্ঘ্য ও প্রস্থ উভয়কেই অর্ধেক করত তখন তার ছবির কাগজের ক্ষেত্রফলের কী পরিবর্তন হতো হিসাব করে লিখি।

উত্তর –
আয়তক্ষেত্রাকার কাগজের দৈর্ঘ্য 15 সেমি এবং প্রস্থ 8 সেমি।
∴ কাগজের ক্ষেত্রফল = (15 × 8)বর্গসেমি = 120 বর্গসেমি

(a) যদি দীপু আয়তক্ষেত্রাকার কাগজের প্রস্থ একই রেখে দৈর্ঘ্য দ্বিগুন করত তবে,
দৈর্ঘ্য = (2 × 15) সেমি = 30 সেমি এবং প্রস্থ = 8 সেমি
∴ নতুন কাগজের ক্ষেত্রফল = (30 × 8)বর্গসেমি = 240 বর্গসেমি
∴ দৈর্ঘ্য দ্বিগুন হলে ক্ষেত্রফল দ্বিগুন হবে।

(b) যদি দীপু আয়তক্ষেত্রাকার কাগজের দৈর্ঘ্য একই রেখে প্রস্থ দ্বিগুন করত তবে,
দৈর্ঘ্য = 15 সেমি এবং প্রস্থ = (2 × 8) সেমি = 16 সেমি
∴ নতুন কাগজের ক্ষেত্রফল = (15 × 16)বর্গসেমি = 240 বর্গসেমি
∴ প্রস্থ দ্বিগুন হলে ক্ষেত্রফল দ্বিগুন হবে।

(c) যদি দীপু তার ছবির কাগজের দৈর্ঘ্য ও প্রস্থ উভয়কেই দ্বিগুন করত তখন,
দৈর্ঘ্য = (2 × 15) সেমি = 30 সেমি এবং প্রস্থ = (2 × 8) সেমি = 16 সেমি
∴ নতুন কাগজের ক্ষেত্রফল = (30 × 16)বর্গসেমি = 480 বর্গসেমি
∴ দৈর্ঘ্য ও প্রস্থ উভয় দ্বিগুন হলে ক্ষেত্রফল 4 গুন হবে।

(d) দীপু যদি তার কাগজের দৈর্ঘ্য ও প্রস্থ উভয়কেই অর্ধেক করত তখন,
দৈর্ঘ্য = \frac{15}2সেমি এবং প্রস্থ = \frac82=4সেমি
∴ নতুন কাগজের ক্ষেত্রফল = \frac{15}2\times4=30বর্গসেমি
∴ দৈর্ঘ্য ও প্রস্থ উভয় অর্ধেক হলে ক্ষেত্রফল \frac14 গুন হবে।

7. আমি তিনটি বর্গক্ষেত্রাকার কাগজ কাটি এবং ক্ষেত্রফলের কীরূপ পরিবর্তন হবে দেখি।
যদি, (a) দৈর্ঘ্য দ্বিগুন করা হয়,
(b) দৈর্ঘ্য অর্ধেক করা হয়।

উত্তর –
মনেকরি, তিনটি বর্গক্ষেত্রাকার কাগজের দৈর্ঘ্য 1 মিটার, 9 মিটার, 2.5 মিটার

(a)  প্রথম কাগজের ক্ষেত্রে,
ক্ষেত্রফল = (1× 1) বর্গমিটার
দৈর্ঘ্য দ্বিগুন করায় নতুন দৈর্ঘ্য = (2 × 1)মিটার
∴ নতুন কাগজের ক্ষেত্রফল =(2 × 1) × (2 × 1) বর্গমিটার
= 2 × 2 × 1 × 1 বর্গমিটার
= 4 × (1 × 1) বর্গমিটার
অর্থাৎ, বর্গক্ষেত্রাকার কাগজের দৈর্ঘ্য 2 গুন করলে ক্ষেত্রফল 4 গুন হয়।

দ্বিতীয় কাগজের ক্ষেত্রে,
ক্ষেত্রফল = (9 × 9) বর্গমিটার
দৈর্ঘ্য দ্বিগুন করায় নতুন দৈর্ঘ্য = (2 × 9)মিটার
∴ নতুন কাগজের ক্ষেত্রফল =(2 × 9) × (2 × 9) বর্গমিটার
= 2 × 2 × 9 × 9 বর্গমিটার
= 4 × (9 × 9) বর্গমিটার
অর্থাৎ, বর্গক্ষেত্রাকার কাগজের দৈর্ঘ্য 2 গুন করলে ক্ষেত্রফল 4 গুন হয়।

তৃতীয় কাগজের ক্ষেত্রে,
ক্ষেত্রফল = (2.5 × 2.5) বর্গমিটার
দৈর্ঘ্য দ্বিগুন করায় নতুন দৈর্ঘ্য = (2 × 2.5)মিটার
∴ নতুন কাগজের ক্ষেত্রফল =(2 × 2.5) × (2 × 2.5) বর্গমিটার
= 2 × 2 × 2.5 × 2.5 বর্গমিটার
= 4 × (2.5 × 2.5) বর্গমিটার
অর্থাৎ, বর্গক্ষেত্রাকার কাগজের দৈর্ঘ্য 2 গুন করলে ক্ষেত্রফল 4 গুন হয়।

(b) প্রথম কাগজের ক্ষেত্রে,
ক্ষেত্রফল = (1× 1) বর্গমিটার
দৈর্ঘ্য অর্ধেক করায় নতুন দৈর্ঘ্য = \frac12\times1মিটার
∴ নতুন কাগজের ক্ষেত্রফল =\left(\frac12\times1\right)\times\left(\frac12\times1\right)=\frac12\times\frac12\times1\times1=\frac14\times\left(1\times1\right)বর্গমিটার
অর্থাৎ, বর্গক্ষেত্রাকার কাগজের দৈর্ঘ্য অর্ধেক করলে ক্ষেত্রফল \frac14 গুন হয়।

দ্বিতীয় কাগজের ক্ষেত্রে,
ক্ষেত্রফল = (9× 9) বর্গমিটার
দৈর্ঘ্য অর্ধেক করায় নতুন দৈর্ঘ্য = \left(\frac12\times9\right)মিটার
∴ নতুন কাগজের ক্ষেত্রফল =\left(\frac12\times9\right)\times\left(\frac12\times9\right)=\frac12\times\frac12\times9\times9=\frac14\times\left(9\times9\right)বর্গমিটার
অর্থাৎ, বর্গক্ষেত্রাকার কাগজের দৈর্ঘ্য অর্ধেক করলে ক্ষেত্রফল \frac14 গুন হয়।

তৃতীয় কাগজের ক্ষেত্রে,
ক্ষেত্রফল = (2.5 × 2.5)বর্গমিটার
দৈর্ঘ্য অর্ধেক করায় নতুন দৈর্ঘ্য = \left(\frac12\times2.5\right) মিটার
∴ নতুন কাগজের ক্ষেত্রফল =\left(\frac12\times2.5\right)\times\left(\frac12\times2.5\right)=\frac12\times\frac12\times2.5\times2.5=\frac14\times\left(2.5\times2.5\right) বর্গমিটার
অর্থাৎ, বর্গক্ষেত্রাকার কাগজের দৈর্ঘ্য অর্ধেক করলে ক্ষেত্রফল \frac14 গুন হয়।

8. আমাদের পাড়ার ক্লাবঘরের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 7.2 মিটার, 5.5 মিটার ও 4.2 মিটার। ঘরে 3 মিটার লম্বা ও 1.8 মিটার চওড়া 1 টি দরজা এবং 2.25 মিটার লম্বা ও 1.8 মিটার চওড়া মাপের 2 টি জানালা আছে।

(a) ক্লাবঘরের মেঝের ক্ষেত্রফল কত হিসাব করি। মেঝে সিমেন্ট করতে প্রতি বর্গমিটারে 62 টাকা হিসাবে কত খরচ পড়বে তা হিসাব করে দেখি।

(b) দরজা ও জানালা বাদে ভিতরের চার দেয়ালের ক্ষেত্রফল হিসাব করে লিখি।

(c) ঘরের ভিতরের ছাদের ক্ষেত্রফল হিসাব করে লিখি।

(d) প্রতি বর্গমিটার 12 টাকা হিসাবে দরজা ও জানালা বাদে ঘরের ভিতরের দিকের চার দেয়াল ও ছাদ চুনকাম করতে কত খরচ পড়বে হিসাব করে লিখি।

উত্তর –
(a) ক্লাবঘরের মেঝের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 7.2 মিটার ও 5.5 মিটার।
∴ ক্লাবঘরের মেঝের ক্ষেত্রফল = 7.2 × 5.5 বর্গমিটার = 39.6 বর্গমিটার
∴ 39.6 বর্গমিটার মেঝে সিমেন্ট করতে খরচ পড়বে = 62 × 39.6 টাকা = 2455.20 টাকা

(b) দরজা ও জানালাসহ চার দেয়ালের ক্ষেত্রফল = 2 × (দৈর্ঘ্য + প্রস্থ ) × উচ্চতা
= 2 × (7.2 + 5.5) × 4.2 বর্গমিটার
= 2 × 12.7 × 4.2 বর্গমিটার = 106.68 বর্গমিটার

1 টি দরজার ক্ষেত্রফল = 3 × 1.8 বর্গমিটার = 5.4 বর্গমিটার
2 টি জানালার ক্ষেত্রফল = 2 × 2.25 × 1.8 বর্গমিটার = 8.1 বর্গমিটার
∴ দরজা ও জানালা বাদে ভিতরের চার দেয়ালের ক্ষেত্রফল = 106.68 – (5.4 + 8.1) বর্গমিটার
= 106.68 – 13.5 বর্গমিটার
= 93.18 বর্গমিটার

(c) ঘরের ভিতরের ছাদের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 7.2 মিটার ও 5.5 মিটার।
∴ ঘরের ভিতরের ছাদের ক্ষেত্রফল = 7.2 × 5.5 বর্গমিটার = 39.6 বর্গমিটার

(d) দরজা ও জানালা বাদে ভিতরের চার দেয়াল ও ছাদের ক্ষেত্রফল = 93.18 + 39.6 বর্গমিটার = 132.78 বর্গমিটার
∴ দরজা ও জানালা বাদে ঘরের ভিতরের দিকের চার দেয়াল ও ছাদ চুনকাম করতে খরচ পড়বে = 12 × 132.78 টাকা = 1593.36 টাকা

কষে দেখি – 1.2

1. নীচের প্রত্যেকটির n–তম ( n ধনাত্মক পূর্ণসংখ্যা ) সজ্জায় প্রয়োজনীয় কাঠির সংখ্যা লিখি –

(i) n–তম সজ্জায় প্রয়োজনীয় কাঠির সংখ্যা = (1 + 5n)

(ii) n–তম সজ্জায় প্রয়োজনীয় কাঠির সংখ্যা = (2 + 5n)

(iii) n–তম সজ্জায় প্রয়োজনীয় কাঠির সংখ্যা = (1 + 4n)

2. একটি সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য (4y + 2)সেমি হলে ত্রিভুজটির পরিসীমা লিখি।

উত্তর –
সমবাহু ত্রিভুজের পরিসীমা = 3 × বাহুর দৈর্ঘ্য
∴ ত্রিভুজটির পরিসীমা = 3 ×(4y + 2) সেমি = (12y + 6) সেমি

3. একটি আয়তখেত্রের দৈর্ঘ্য (8x + 3y)সেমি এবং (8x – 3y)প্রস্থ সেমি। ওই আয়তখেত্রের ক্ষেত্রফল লিখি।

উত্তর –
আয়তখেত্রের ক্ষেত্রফল = দৈর্ঘ্য × প্রস্থ
∴ আয়তখেত্রটির ক্ষেত্রফল = (8x + 3y) (8x – 3y)বর্গসেমি
={(8x)² – (3y)²}  [∵ (a + b)(a – b)= a² – b²]
={64x² – 9y² } বর্গসেমি

4. বর্গক্ষেত্রের একটি বাহুর দৈর্ঘ্য (3m – 4)মিটার হলে ক্ষেত্রফল কত হবে m-এর মাধ্যমে লিখি। m-এর মান কত হলে এই বর্গক্ষেত্রের পরিসীমা 8 মিটার হবে হিসাব করে লিখি।

উত্তর –
বর্গক্ষেত্রের ক্ষেত্রফল = বাহু × বাহু
∴ বর্গক্ষেত্রটির ক্ষেত্রফল =(3m – 4) (3m – 4) বর্গমিটার =\left(3m-4\right)^2বর্গমিটার
বর্গক্ষেত্রের পরিসীমা = 4(3m – 4)মিটার

প্রশ্নানুসারে,

\[\text{4}\left( \text{3m }\text{ 4} \right)=8\]

\[\Rightarrow 12m-16=8\]

\[\Rightarrow 12m=8+16\]

\[\Rightarrow 12m=24\]

\[\therefore m=\frac{24}{12}=2\]

অর্থাৎ, m-এর মান 2 হলে এই বর্গক্ষেত্রের পরিসীমা 8 মিটার হবে

5.

বীজগানিতি সংখ্যামালা	যোগ করি	বিয়োগ করি
\[\left( a \right)\left( i \right){{x}^{2}}+2{{y}^{2}}\] \[\left( ii \right)\left( -8{{y}^{2}}+6{{x}^{2}}+{{z}^{2}} \right)\]	\[\left( i \right)+\left( ii \right)\] \[{{x}^{2}}+2{{y}^{2}}+\left( -8{{y}^{2}}+6{{x}^{2}}+{{z}^{2}} \right)\] \[={{x}^{2}}+2{{y}^{2}}-8{{y}^{2}}+6{{x}^{2}}+{{z}^{2}}\] \[=7{{x}^{2}}-6{{y}^{2}}+{{z}^{2}}\]	\[\left( i \right)-\left( ii \right)\] \[{{x}^{2}}+2{{y}^{2}}-\left( -8{{y}^{2}}+6{{x}^{2}}+{{z}^{2}} \right)\] \[={{x}^{2}}+2{{y}^{2}}+8{{y}^{2}}-6{{x}^{2}}-{{z}^{2}}\] \[=10{{y}^{2}}-5{{x}^{2}}-{{z}^{2}}\]
\[\left( b \right)\left( i \right)6{{a}^{2}}+2,\] \[\left( ii \right)-3{{a}^{2}}+3a,\] \[\left( iii \right)-2a+3\]	\[\left( i \right)+\left( ii \right)+\left( iii \right)\]	\[\left( ii \right)-\left( i \right)\] \[\left( iii \right)-\left( i \right)\]
\[\left( c \right)\left( i \right)9{{m}^{2}}-2mn+{{n}^{2}}\] \[\left( ii \right){{m}^{2}}+{{n}^{2}}\] \[\left( iii \right){{m}^{2}}-3mn-2{{n}^{2}}\]	\[\left( i \right)+\left( ii \right)+\left( iii \right)\]	\[\left( i \right)-\left( ii \right)\] \[\left( ii \right)-\left( iii \right)\]

উত্তর –

বীজগানিতি সংখ্যামালা	যোগ করি	বিয়োগ করি
\[\left( a \right)\left( i \right){{x}^{2}}+2{{y}^{2}}\] \[\left( ii \right)\left( -8{{y}^{2}}+6{{x}^{2}}+{{z}^{2}} \right)\]	\[\left( i \right)+\left( ii \right)\]\[{{x}^{2}}+2{{y}^{2}}+\left( -8{{y}^{2}}+6{{x}^{2}}+{{z}^{2}} \right)\] \[={{x}^{2}}+2{{y}^{2}}-8{{y}^{2}}+6{{x}^{2}}+{{z}^{2}}\] \[=7{{x}^{2}}-6{{y}^{2}}+{{z}^{2}}\]	\[\left( i \right)-\left( ii \right)\] \[{{x}^{2}}+2{{y}^{2}}-\left( -8{{y}^{2}}+6{{x}^{2}}+{{z}^{2}} \right)\] \[={{x}^{2}}+2{{y}^{2}}+8{{y}^{2}}-6{{x}^{2}}-{{z}^{2}}\] \[=10{{y}^{2}}-5{{x}^{2}}-{{z}^{2}}\]
\[\left( b \right)\left( i \right)6{{a}^{2}}+2,\] \[\left( ii \right)-3{{a}^{2}}+3a,\] \[\left( iii \right)-2a+3\]	\[\left( i \right)+\left( ii \right)+\left( iii \right)\] \[3{{a}^{2}}+a+5\]	\[\left( ii \right)-\left( i \right)\] \[-9{{a}^{2}}+3a-2\] \[\left( iii \right)-\left( i \right)\] \[-6{{a}^{2}}-2a+1\]
\[\left( c \right)\left( i \right)9{{m}^{2}}-2mn+{{n}^{2}}\] \[\left( ii \right){{m}^{2}}+{{n}^{2}}\] \[\left( iii \right){{m}^{2}}-3mn-2{{n}^{2}}\]	\[\left( i \right)+\left( ii \right)+\left( iii \right)\] \[11{{m}^{2}}-5mn\]	\[\left( i \right)-\left( ii \right)=8{{m}^{2}}-2mn\] \[\left( ii \right)-\left( iii \right)=3mn+3{{n}^{2}}\]

6.

বীজগানিতি সংখ্যামালা	গুন করি	ভাগ করি
\[\left( a \right)\left( i \right)9{{a}^{3}}{{b}^{2}}-15{{a}^{2}}{{b}^{3}}\] \[\left( b \right)3ab\]	\[\left( i \right)\times \left( ii \right)\] \[\left( 9{{a}^{3}}{{b}^{2}}-15{{a}^{2}}{{b}^{3}} \right)\times 3ab\] \[=27{{a}^{4}}{{b}^{3}}-45{{a}^{3}}{{b}^{4}}\]	\[\left( i \right)\div \left( ii \right)\] \[\frac{9{{a}^{3}}{{b}^{2}}-15{{a}^{2}}{{b}^{3}}}{3ab}\] \[=\frac{9{{a}^{3}}{{b}^{2}}}{3ab}-\frac{15{{a}^{2}}{{b}^{3}}}{3ab}\] \[=3{{a}^{2}}b-5a{{b}^{2}}\]
\[\left( b \right)\left( i \right){{x}^{4}}-4{{x}^{3}}+6{{x}^{2}}\] \[\left( ii \right){{x}^{2}}\]	\[\left( i \right)\times \left( ii \right)\]	\[\left( i \right)\div \left( ii \right)\]
\[\left( i \right)3{{m}^{2}}{{n}^{3}}+40{{m}^{3}}{{n}^{4}}-5{{m}^{4}}{{n}^{5}}\] \[\left( ii \right)10{{m}^{2}}{{n}^{2}}\]	\[\left( i \right)\times \left( ii \right)\]	\[\left( i \right)\div \left( ii \right)\]
\[\left( c \right)\left( i \right)\left( 49{{l}^{2}}-100{{m}^{2}} \right)\] \[\left( ii \right)\left( 7l+10m \right)\]	\[\left( i \right)\times \left( ii \right)\]	\[\left( i \right)\div \left( ii \right)\]   [\[{{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)\] সূত্রের সাহায্যে ]
\[\left( d \right)\left( i \right)625{{a}^{4}}-81{{b}^{4}}\] \[\left( ii \right)5a+3b\]	\[\left( i \right)\times \left( ii \right)\]	\[\left( i \right)\div \left( ii \right)\]   [\[{{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right)\] সূত্রের সাহায্যে ]

উত্তর –

বীজগানিতি সংখ্যামালা	গুন করি	ভাগ করি
\[\left( a \right)\left( i \right)9{{a}^{3}}{{b}^{2}}-15{{a}^{2}}{{b}^{3}}\] \[\left( b \right)3ab\]	\[\left( i \right)\times \left( ii \right)\] \[\left( 9{{a}^{3}}{{b}^{2}}-15{{a}^{2}}{{b}^{3}} \right)\times 3ab\] \[=27{{a}^{4}}{{b}^{3}}-45{{a}^{3}}{{b}^{4}}\]	\[\left( i \right)\div \left( ii \right)\] \[\frac{9{{a}^{3}}{{b}^{2}}-15{{a}^{2}}{{b}^{3}}}{3ab}\] \[=\frac{9{{a}^{3}}{{b}^{2}}}{3ab}-\frac{15{{a}^{2}}{{b}^{3}}}{3ab}\] \[=3{{a}^{2}}b-5a{{b}^{2}}\]
\[\left( b \right)\left( i \right){{x}^{4}}-4{{x}^{3}}+6{{x}^{2}}\] \[\left( ii \right){{x}^{2}}\]	\[\left( i \right)\times \left( ii \right)\] \[\left( {{x}^{4}}-4{{x}^{3}}+6{{x}^{2}} \right)\times {{x}^{2}}\] \[={{x}^{6}}-4{{x}^{5}}+6{{x}^{4}}\]	\[\left( i \right)\div \left( ii \right)\] \[\frac{{{x}^{4}}-4{{x}^{3}}+6{{x}^{2}}}{{{x}^{2}}}\] \[={{x}^{2}}-4x+6\]
\[\left( i \right)3{{m}^{2}}{{n}^{3}}+40{{m}^{3}}{{n}^{4}}-5{{m}^{4}}{{n}^{5}}\] \[\left( ii \right)10{{m}^{2}}{{n}^{2}}\]	\[\left( i \right)\times \left( ii \right)\] \[\left( 3{{m}^{2}}{{n}^{3}}+40{{m}^{3}}{{n}^{4}}-5{{m}^{4}}{{n}^{5}} \right)\times 10{{m}^{2}}{{n}^{2}}\] \[=30{{m}^{4}}{{n}^{5}}+400{{m}^{5}}{{n}^{6}}-50{{m}^{6}}{{n}^{7}}\]	\[\left( i \right)\div \left( ii \right)\] \[\frac{3{{m}^{2}}{{n}^{3}}+40{{m}^{3}}{{n}^{4}}-5{{m}^{4}}{{n}^{5}}}{10{{m}^{2}}{{n}^{2}}}\] \[=\frac{3}{10}n+4m{{n}^{2}}-\frac{1}{2}{{m}^{2}}{{n}^{3}}\]
\[\left( c \right)\left( i \right)\left( 49{{l}^{2}}-100{{m}^{2}} \right)\] \[\left( ii \right)\left( 7l+10m \right)\]	\[\left( i \right)\times \left( ii \right)\] \[\left( 49{{l}^{2}}-100{{m}^{2}} \right)\times \left( 7l+10m \right)\] \[=343{{l}^{3}}+490{{l}^{2}}m-700l{{m}^{2}}-1000{{m}^{3}}\]	\[\left( i \right)\div \left( ii \right)\] \[\frac{49{{l}^{2}}-100{{m}^{2}}}{7l+10m}\] \[=\frac{\left( 7l+10m \right)\left( 7l-10m \right)}{\left( 7l+10m \right)}\] \[=\left( 7l-10m \right)\]
\[\left( d \right)\left( i \right)625{{a}^{4}}-81{{b}^{4}}\] \[\left( ii \right)5a+3b\]	\[\left( i \right)\times \left( ii \right)\] \[\left( 625{{a}^{4}}-81{{b}^{4}} \right)\times \left( 5a+3b \right)\] \[=3125{{a}^{5}}+1875{{a}^{4}}b-405a{{b}^{4}}-243{{b}^{5}}\]	\[\left( i \right)\div \left( ii \right)\] \[\frac{625{{a}^{4}}-81{{b}^{4}}}{5a+3b}\] \[=\frac{\left( 25{{a}^{2}}+9{{b}^{2}} \right)\left( 25{{a}^{2}}-9{{b}^{2}} \right)}{\left( 5a+3b \right)}\]\[=\frac{\left( 25{{a}^{2}}+9{{b}^{2}} \right)\left( 5a+3b \right)\left( 5a-3b \right)}{\left( 5a+3b \right)}\]\[=\left( 25{{a}^{2}}+9{{b}^{2}} \right)\left( 5a+3b \right)\]

7.

সরল করি –

\[\left( i \right)\left( a-b \right)+\left( b-c \right)+\left( c-a \right)\]

\[\left( ii \right)\left( a+b \right)\left( a-b \right)+\left( b+c \right)\left( b-c \right)+\left( c+a \right)\left( c-a \right)\]

\[\left( iii \right){{x}^{2}}\times \left( \frac{x}{y}-\frac{y}{x} \right)\times \left( \frac{y}{x}+\frac{x}{y} \right)\times {{y}^{2}}\]

\[\left( iv \right)a\left( b-c \right)+b\left( c-a \right)+c\left( a-b \right)\]

\[\left( iv \right)a\left( b-c \right)+b\left( c-a \right)+c\left( a-b \right)\]

\[\left( v \right){{x}^{2}}\left( {{y}^{2}}-{{z}^{2}} \right)+{{y}^{2}}\left( {{z}^{2}}-{{x}^{2}} \right)+{{z}^{2}}\left( {{x}^{2}}-{{y}^{2}} \right)\]

\[\left( vi \right)\left( {{x}^{3}}+{{y}^{3}} \right)\left( {{x}^{3}}-{{y}^{3}} \right)+\left( {{y}^{3}}+{{z}^{3}} \right)\left( {{y}^{3}}-{{z}^{3}} \right)+\left( {{z}^{3}}+{{x}^{3}} \right)\left( {{z}^{3}}-{{x}^{3}} \right)\]

উত্তর –

\[\left( i \right)\left( a-b \right)+\left( b-c \right)+\left( c-a \right)\]

\[=a-b+b-c+c-a\]

\[=a-a+b-b+c-c\]

\[=0\]

\[\left( ii \right)\left( a+b \right)\left( a-b \right)+\left( b+c \right)\left( b-c \right)+\left( c+a \right)\left( c-a \right)\]

\[={{a}^{2}}-{{b}^{2}}+{{b}^{2}}-{{c}^{2}}+{{c}^{2}}-{{a}^{2}}\]

\[={{a}^{2}}-{{a}^{2}}+{{b}^{2}}-{{b}^{2}}+{{c}^{2}}-{{c}^{2}}\]

\[=0\]

\[\left( iii \right){{x}^{2}}\times \left( \frac{x}{y}-\frac{y}{x} \right)\times \left( \frac{y}{x}+\frac{x}{y} \right)\times {{y}^{2}}\]

\[={{x}^{2}}\times \left\{ {{\left( \frac{x}{y} \right)}^{2}}-{{\left( \frac{y}{x} \right)}^{2}} \right\}\times {{y}^{2}}\]

\[={{x}^{2}}\times \left\{ \frac{{{x}^{2}}}{{{y}^{2}}}-\frac{{{y}^{2}}}{{{x}^{2}}} \right\}\times {{y}^{2}}\]

\[={{x}^{2}}\times \frac{{{x}^{2}}}{{{y}^{2}}}\times {{y}^{2}}-{{x}^{2}}\times \frac{{{y}^{2}}}{{{x}^{2}}}\times {{y}^{2}}\]

\[={{x}^{4}}-{{y}^{4}}\]

\[\left( iv \right)a\left( b-c \right)+b\left( c-a \right)+c\left( a-b \right)\]

\[=ab-ac+bc-ab+ac-bc\]

\[=ab-ab+bc-bc+ac-ac\]

\[=0\]

\[\left( v \right){{x}^{2}}\left( {{y}^{2}}-{{z}^{2}} \right)+{{y}^{2}}\left( {{z}^{2}}-{{x}^{2}} \right)+{{z}^{2}}\left( {{x}^{2}}-{{y}^{2}} \right)\]

\[={{x}^{2}}{{y}^{2}}-{{x}^{2}}{{z}^{2}}+{{y}^{2}}{{z}^{2}}-{{x}^{2}}{{y}^{2}}+{{x}^{2}}{{z}^{2}}-{{y}^{2}}{{z}^{2}}\]

\[={{x}^{2}}{{y}^{2}}-{{x}^{2}}{{y}^{2}}+{{y}^{2}}{{z}^{2}}-{{y}^{2}}{{z}^{2}}+{{x}^{2}}{{z}^{2}}-{{x}^{2}}{{z}^{2}}\]

\[=0\]

\[\left( vi \right)\left( {{x}^{3}}+{{y}^{3}} \right)\left( {{x}^{3}}-{{y}^{3}} \right)+\left( {{y}^{3}}+{{z}^{3}} \right)\left( {{y}^{3}}-{{z}^{3}} \right)+\left( {{z}^{3}}+{{x}^{3}} \right)\left( {{z}^{3}}-{{x}^{3}} \right)\]

\[=\left\{ {{\left( {{x}^{3}} \right)}^{2}}-{{\left( {{y}^{3}} \right)}^{2}} \right\}+\left\{ {{\left( {{y}^{3}} \right)}^{2}}-{{\left( {{z}^{3}} \right)}^{2}} \right\}+\left\{ {{\left( {{z}^{3}} \right)}^{2}}-{{\left( {{x}^{3}} \right)}^{2}} \right\}\]

\[={{x}^{6}}-{{y}^{6}}+{{y}^{6}}-{{z}^{6}}+{{z}^{6}}-{{x}^{6}}\]

\[={{x}^{6}}-{{x}^{6}}-{{y}^{6}}+{{y}^{6}}-{{z}^{6}}+{{z}^{6}}\]

\[=0\]

;