দশম শ্রেণী – অধ্যায় ২৩ : ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি সম্পূর্ণ সমাধান

কষে দেখি – 23.1

1. একটি সমকোণী ত্রিভুজ ABC এঁকেছি যার অতিভুজ AB=10 সেমি, ভূমি BC=8 সেমি এবং লম্ব AC=6 সেমি। ∠ABC-এর Sine এবং tangent-এর মান নির্ণয় করি।

উত্তর –

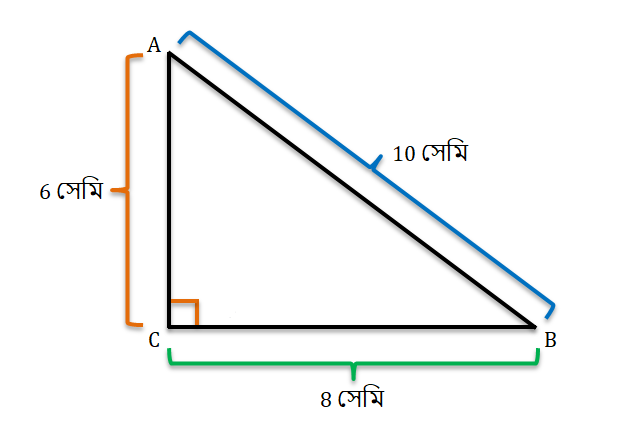
\[\sin \angle ABC=\frac{AC}{AB}=\frac{6}{10}=\frac{3}{5}\]

\[\tan \angle ABC=\frac{AC}{BC}=\frac{6}{8}=\frac{3}{4}\]

2. সোমা একটি সমকোণী ত্রিভুজ ABC এঁকেছে যার ∠ABC = 90°, AB=24 সেমি এবং BC=7 সেমি। হিসাব করে sinA, cosA, tanA ও cosecA-এর মান লিখি।

উত্তর –

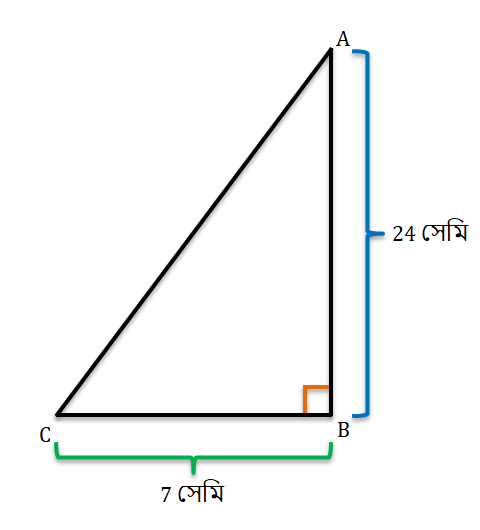
এখানে ABC সমকোনী ত্রিভুজের ∠ABC = 90°, AB=24 সেমি এবং BC=7 সেমি।

\therefore AC=\sqrt{{{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}}=\sqrt{{{\left( 24 \right)}^{2}}+{{\left( 7 \right)}^{2}}}=\sqrt{576+49}=\sqrt{625}=25 সেমি।

\[\sin A=\frac{BC}{AC}=\frac{7}{25}\]\[\cos A=\frac{AB}{AC}=\frac{24}{25}\]\[\tan A=\frac{BC}{AB}=\frac{7}{24}\]\[\cos ecA=\frac{AC}{BC}=\frac{25}{7}\]

3. যদি ABC একটি সমকোণী ত্রিভুজের ∠C=90°, BC=21 একক এবং AB=29 একক হয়, তাহলে sinA, cosA, sinB ও cosB-এর মান নির্ণয় করি।

উত্তর –

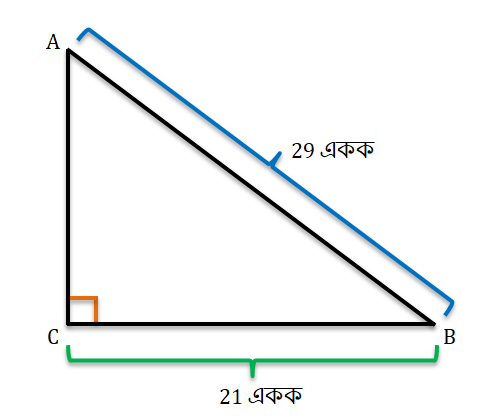
ABC সমকোণী ত্রিভুজের ∠C=90°, BC=21 একক এবং AB=29 একক

\[\therefore AC=\sqrt{{{\left( AB \right)}^{2}}-{{\left( BC \right)}^{2}}}=\sqrt{{{\left( 29 \right)}^{2}}-{{\left( 21 \right)}^{2}}}=\sqrt{\left( 29+21 \right)\left( 29-21 \right)}\]

\[=\sqrt{50\times 8}=\sqrt{5\times 5\times 2\times 2\times 2\times 2}=5\times 2\times 2=20\]

\[\sin A=\frac{BC}{AB}=\frac{21}{29}\]

\[\cos A=\frac{AC}{AB}=\frac{20}{29}\]

\[\sin B=\frac{AC}{AB}=\frac{20}{29}\]

\[\cos B=\frac{BC}{AB}=\frac{21}{29}\]

4. যদি \cos \theta =\frac{7}{25} হয়, তাহলে θ কোণের সকল ত্রিকোণমিতিক অনুপাতের মান নির্ণয় করি।

উত্তর –

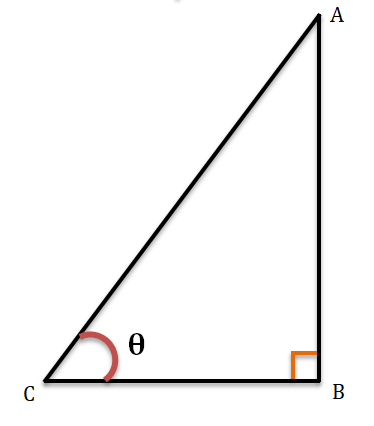
ABC সমকোনী ত্রিভুজের ∠ABC = 90°, ∠ACB = θ

\[\cos \theta =\frac{BC}{AC}=\frac{7}{25}\] 

মনেকরি, ভূমি BC = 7k একক এবং অতিভুজ  AC = 25k একক [ যেখানে k > 0]

∴ লম্ব AB=\sqrt{{{\left( AC \right)}^{2}}-{{\left( BC \right)}^{2}}}=\sqrt{{{\left( 25k \right)}^{2}}-{{\left( 7k \right)}^{2}}}

=\sqrt{625{{k}^{2}}-49{{k}^{2}}}=\sqrt{576{{k}^{2}}}=24k একক

\[\sin \theta =\frac{AB}{AC}=\frac{24k}{25k}=\frac{24}{25}\]

\[\tan \theta =\frac{AB}{BC}=\frac{24k}{7k}=\frac{24}{7}\]

\[\cos ec\theta =\frac{AC}{AB}=\frac{25k}{24k}=\frac{25}{24}\]

\[\sec \theta =\frac{AC}{BC}=\frac{25k}{7k}=\frac{25}{7}\]

\[\cot \theta =\frac{BC}{AB}=\frac{7k}{24k}=\frac{7}{24}\]

5. যদি cotθ=2 হয়, তাহলে tanθ ও secθ-এর মান নির্ণয় করি এবং দেখাই যে, 1 + tan²θ = sec²θ

উত্তর –

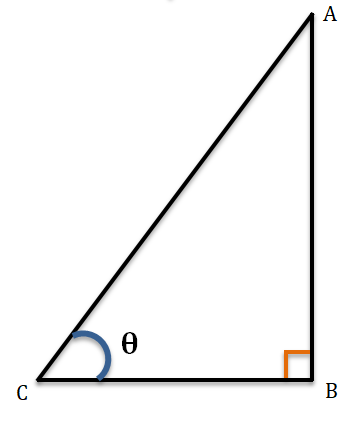
ABC সমকোনী ত্রিভুজের ∠ABC = 90°, ∠ACB = θ

\[\cot \theta =\frac{BC}{AB}=\frac{2}{1}\]

মনেকরি, ভূমি BC = 2k একক এবং অতিভুজ  AB = k একক [ যেখানে k > 0]

∴ অতিভুজ AC=\sqrt{{{\left( AB \right)}^{2}}+{{\left( BC \right)}^{2}}}=\sqrt{{{\left( k \right)}^{2}}+{{\left( 2k \right)}^{2}}}

=\sqrt{{{k}^{2}}+4{{k}^{2}}}=\sqrt{5{{k}^{2}}}=\sqrt{5}k একক

\[\tan \theta =\frac{AB}{BC}=\frac{k}{2k}=\frac{1}{2}\] 

\[\sec \theta =\frac{AC}{BC}=\frac{\sqrt{5}k}{2k}=\frac{\sqrt{5}}{2}\]

বামপক্ষ, 1+{{\tan }^{2}}\theta =1+{{\left( \frac{1}{2} \right)}^{2}}=1+\frac{1}{4}=\frac{5}{4}

ডানপক্ষ, {{\sec }^{2}}\theta ={{\left( \frac{\sqrt{5}}{2} \right)}^{2}}=\frac{5}{4}

∴ বামপক্ষ = ডানপক্ষ (প্রমানিত)।

6. cos θ=0.6 হলে, দেখাই যে, (5sinθ – 3tanθ) = 0

উত্তর –

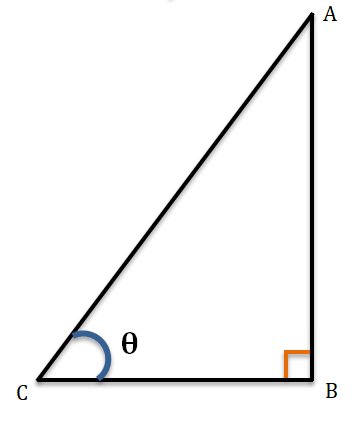
ABC সমকোনী ত্রিভুজের ∠ABC = 90°, ∠ACB = θ

\[\cos \theta =0.6=\frac{6}{10}=\frac{3}{5}\]

মনেকরি, ভূমি BC = 3k একক এবং অতিভুজ  AC = 5k একক [ যেখানে k > 0]

∴ লম্বAB=\sqrt{{{\left( AC \right)}^{2}}-{{\left( BC \right)}^{2}}}=\sqrt{{{\left( 5k \right)}^{2}}-{{\left( 3k \right)}^{2}}}

=\sqrt{25{{k}^{2}}-9{{k}^{2}}}=\sqrt{16{{k}^{2}}}=4k] একক

\[\sin \theta =\frac{AB}{AC}=\frac{4k}{5k}=\frac{4}{5}\]

\[\tan \theta =\frac{AB}{BC}=\frac{4k}{3k}=\frac{4}{3}\]

বামপক্ষ, 5\sin \theta -3\tan \theta =5\times \frac{4}{5}-3\times \frac{4}{3}=4-4=0

∴ বামপক্ষ = ডানপক্ষ (প্রমানিত)।

7. যদি \cot A=\frac{4}{7.5} হয়, তাহলে cosA এবং cosecA-এর মান নির্ণয় করি এবং দেখাই যে, 1 + cot²A = cosec²A

উত্তর –

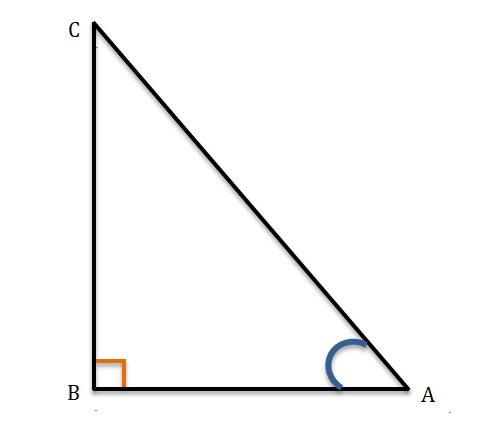
ABC সমকোনী ত্রিভুজের ∠ABC = 90°

\[\cot A=\frac{BA}{BC}=\frac{4}{7.5}=\frac{4\times 10}{75}=\frac{8}{15}\]

মনেকরি, ভূমি BA = 8k একক এবং লম্ব BC = 15k একক [ যেখানে k > 0]

∴ অতিভুজ AC=\sqrt{{{\left( BC \right)}^{2}}+{{\left( BA \right)}^{2}}}=\sqrt{{{\left( 15k \right)}^{2}}+{{\left( 8k \right)}^{2}}}

=\sqrt{225{{k}^{2}}+64{{k}^{2}}}=\sqrt{289{{k}^{2}}}=17k একক

\[\cos A=\frac{BA}{AC}=\frac{8k}{17k}=\frac{8}{17}\]

\[\cos ecA=\frac{AC}{BC}=\frac{17k}{15k}=\frac{17}{15}\]

বামপক্ষ, 1+{{\cot }^{2}}A=1+{{\left( \frac{8}{15} \right)}^{2}}=1+\frac{64}{225}=\frac{289}{225}

ডানপক্ষ, \cos e{{c}^{2}}A={{\left( \frac{17}{15} \right)}^{2}}=\frac{289}{225}

∴ বামপক্ষ = ডানপক্ষ (প্রমানিত)।

8. যদি \sin C=\frac{2}{3} হয়, তবে cosC × cosecC-এর মান হিসাব করে লিখি।

উত্তর –

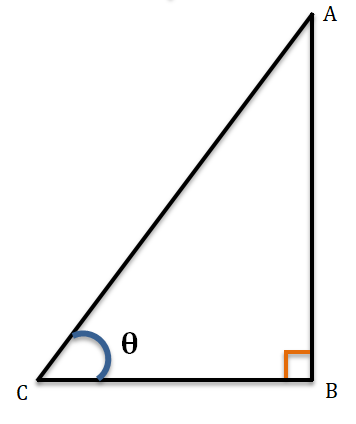
ABC সমকোনী ত্রিভুজের ∠ABC = 90°

\[\sin C=\frac{AB}{AC}=\frac{2}{3}\]

মনেকরি, লম্ব AB = 2k একক এবং অতিভুজ AC = 15k একক [ যেখানে k > 0]

∴ ভূমি BC=\sqrt{{{\left( AC \right)}^{2}}-{{\left( AB \right)}^{2}}}=\sqrt{{{\left( 3k \right)}^{2}}-{{\left( 2k \right)}^{2}}}

=\sqrt{9{{k}^{2}}-4{{k}^{2}}}=\sqrt{5{{k}^{2}}}=\sqrt{5}k একক

\[\cos C=\frac{BC}{AC}=\frac{\sqrt{5}k}{3k}=\frac{\sqrt{5}}{3}\]

\[\cos ec\,C=\frac{AC}{AB}=\frac{3k}{2k}=\frac{3}{2}\]

\[\therefore \text{cos C}\times \text{ cosec C}=\frac{\sqrt{5}}{3}\times \frac{3}{2}=\frac{\sqrt{5}}{2}\]

9. নীচের বিবৃতিগুলি সত্য না মিথ্যা তা যুক্তি সহকারে লিখি।

(i) tanA-এর মান সর্বদা 1 অপেক্ষা 1 বড়ো।

উত্তর – মিথ্যা। লম্ব, ভুমির থেকে সব সময় বড়ো নাও হতে পারে।

(ii) cotA-এর মান সর্বদা 1 অপেক্ষা ছোটো।

উত্তর – মিথ্যা। ভুমি, লম্বের থেকে সব সময় বড়ো নাও হতে পারে।

(iii) একটি কোণ θ-এর জন্য \sin \theta =\frac{4}{3} হতে পারে।

উত্তর – মিথ্যা। লম্ব, অতিভুজের থেকে বড়ো হতে পারে না।

(iv) একটি কোণ α-এর জন্য \sec \alpha =\frac{12}{5} হতে পারে।

উত্তর – সত্য। অতিভুজ, ভূমির থেকে বড়ো হতে পারে।

(v) একটি কোণ β-এর জন্য \cos ec\beta =\frac{5}{13} হতে পারে।

উত্তর – মিথ্যা। অতিভুজের মান লম্বের থেকে সর্বদা বড়ো হয়।

(vi) একটি কোণ θ-এর জন্য \cos \theta =\frac{3}{5} হতে পারে।

উত্তর – সত্য। অতিভুজের মান ভূমির থেকে সর্বদা বড়ো হয়।

কষে দেখি - 23.2

1. আমাদের বাড়ির জানালায় একটি মই ভূমির সঙ্গে 60° কোণে রাখা আছে। মইটি 2\sqrt{3} মিটার লম্বা হলে আমাদের ওই জানালাটি ভূমি থেকে কত উপরে আছে ছবি এঁকে হিসাব করে লিখি। 

উত্তর –

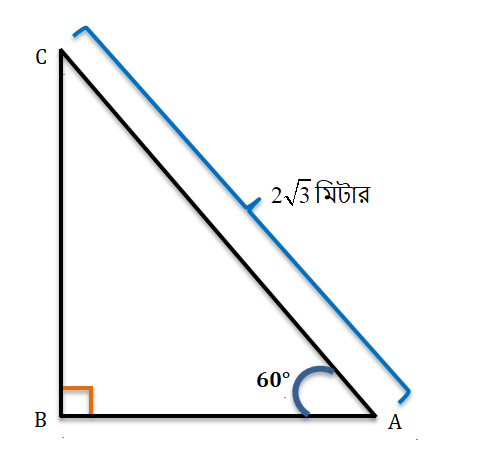
মনেকরি, BC হল ভূমি থেকে জানালার উচ্চতা এবং AC = 2\sqrt{3}মিটার লম্বা মই এবং ∠BAC = 60°।

ABC সমকোনী ত্রিভুজের

\[\frac{BC}{AC}=\sin 60{}^\circ \]

\[\Rightarrow \frac{BC}{2\sqrt{3}}=\frac{\sqrt{3}}{2}\]

\[\therefore BC=\frac{\sqrt{3}}{2}\times 2\sqrt{3}=3\]

∴ জানালাটি ভূমি থেকে 3 মিটার উপরে আছে।

2. ABC সমকোণী ত্রিভুজের ∠B সমকোণ। AB= 8\sqrt{3}সেমি এবং BC=8 সেমি হলে, ∠ACB ও ∠BAC-এর মান হিসাব করে লিখি।

উত্তর –

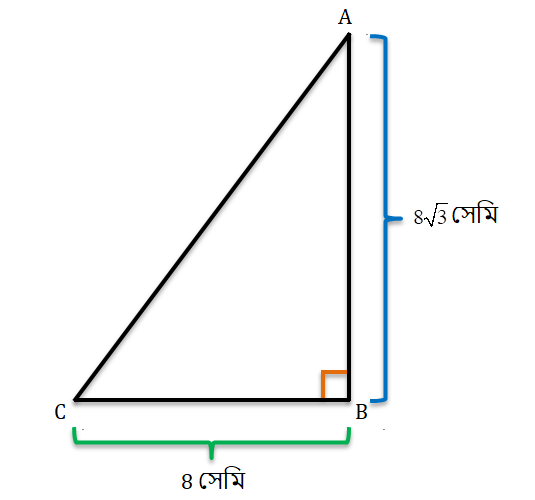
ABC সমকোণী ত্রিভুজের ∠B সমকোণ। AB=8\sqrt{3}সেমি এবং BC=8 সেমি।

\[\tan \angle ACB=\frac{AB}{BC}\]

\[\Rightarrow \tan \angle ACB=\frac{8\sqrt{3}}{8}\]

\[\Rightarrow \tan \angle ACB=\sqrt{3}\]

\[\Rightarrow \tan \angle ACB=\tan \,60{}^\circ \]

\[\therefore \angle ACB=60{}^\circ \]

আবার,

\[\cot \angle BAC=\frac{AB}{BC}\]

\[\Rightarrow \cot \angle BAC=\frac{8\sqrt{3}}{8}\]

\[\Rightarrow \cot \angle BAC=\sqrt{3}\]

\[\Rightarrow \cot \angle BAC=\cot \,30{}^\circ \]

\[\therefore \angle BAC=30{}^\circ \]

∴ ∠ACB ও ∠BAC-এর মান যথাক্রমে 60° এবং 30°।

3. ABC সমকোণী ত্রিভুজের ∠B=90°, ∠A=30° এবং AC=20 সেমি। BC এবং AB বাহুদ্বয়ের দৈর্ঘ্য হিসাব করে লিখি।

উত্তর –

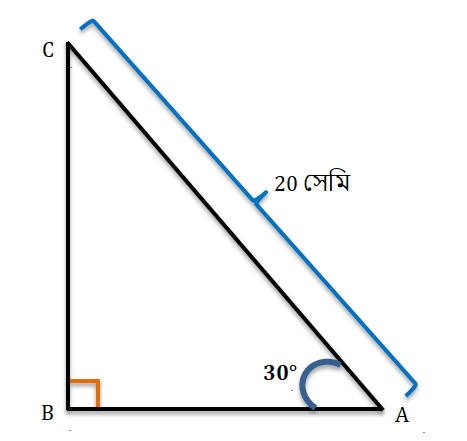
ABC সমকোণী ত্রিভুজের ∠B=90°, ∠A=30° এবং AC=20 সেমি।

\[\frac{AB}{AC}=\cos \,30{}^\circ \]

\[\Rightarrow \frac{AB}{20}=\frac{\sqrt{3}}{2}\]

\[\therefore AB=\frac{\sqrt{3}}{2}\times 20=10\sqrt{3}\]

আবার,

\[\frac{BC}{AC}=\sin \,30{}^\circ \]

\[\Rightarrow \frac{BC}{20}=\frac{1}{2}\]

\[\therefore BC=\frac{1}{2}\times 20=10\]

∴ BC এবং AB বাহুদ্বয়ের দৈর্ঘ্য যথাক্রমে 10 সেমি এবং 10\sqrt{3}সেমি।

4. PQR সমকোণী ত্রিভুজের ∠Q=90°, ∠R=45°; যদি PR= 3\sqrt{2} মিটার হয়, তাহলে PQ ও QR বাহুদ্বয়ের দৈর্ঘ্য নির্ণয় করি।

উত্তর –

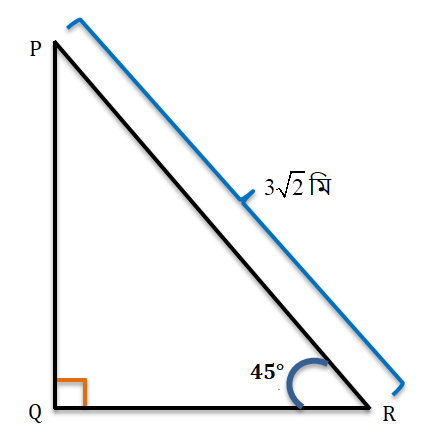
PQR সমকোণী ত্রিভুজের ∠Q=90°, ∠R=45°; যদি PR=3\sqrt{2}মিটার।

\[\frac{PQ}{PR}=\sin \,45{}^\circ \]

\[\Rightarrow \frac{PQ}{3\sqrt{2}}=\frac{1}{\sqrt{2}}\]

\[\therefore PQ=\frac{1}{\sqrt{2}}\times 3\sqrt{2}=3\]

আবার,

\[\frac{QR}{PR}=\cos \,45{}^\circ \]

\[\Rightarrow \frac{QR}{3\sqrt{2}}=\frac{1}{\sqrt{2}}\]

\[\therefore QR=\frac{1}{\sqrt{2}}\times 3\sqrt{2}=3\]

∴ PQ ও QR বাহুদ্বয়ের দৈর্ঘ্য যথাক্রমে 3 মিটার এবং 3 মিটার ।

5. মান নির্ণয় করি -

(i) {{\sin }^{2}}45{}^\circ -\cos e{{c}^{2}}60{}^\circ +{{\sec }^{2}}30{}^\circ

উত্তর –

\[{{\sin }^{2}}45{}^\circ -\cos e{{c}^{2}}60{}^\circ +{{\sec }^{2}}30{}^\circ \]

\[={{\left( \frac{1}{\sqrt{2}} \right)}^{2}}-{{\left( \frac{2}{\sqrt{3}} \right)}^{2}}+{{\left( \frac{2}{\sqrt{3}} \right)}^{2}}\].

\[=\frac{1}{2}\]

∴ নির্নেয় মান = \frac{1}{2}

(ii) {{\sec }^{2}}45{}^\circ -{{\cot }^{2}}45{}^\circ -{{\sin }^{2}}30{}^\circ -{{\sin }^{3}}60{}^\circ

উত্তর –

\[{{\sec }^{2}}45{}^\circ -{{\cot }^{2}}45{}^\circ -{{\sin }^{2}}30{}^\circ -{{\sin }^{2}}60{}^\circ \]

\[={{\left( \sqrt{2} \right)}^{2}}-{{\left( 1 \right)}^{2}}-{{\left( \frac{1}{2} \right)}^{2}}-{{\left( \frac{\sqrt{3}}{2} \right)}^{2}}\]

\[=2-1-\frac{1}{4}-\frac{3}{4}\]

\[=\frac{8-4-1-3}{4}=\frac{0}{4}=0\]

∴ নির্নেয় মান = 0

(iii) 3{{\tan }^{2}}45{}^\circ -{{\sin }^{2}}60{}^\circ -\frac{1}{3}{{\cot }^{2}}30{}^\circ -\frac{1}{8}{{\sec }^{2}}45{}^\circ

উত্তর –

\[3{{\tan }^{2}}45{}^\circ -{{\sin }^{2}}60{}^\circ -\frac{1}{3}{{\cot }^{2}}30{}^\circ -\frac{1}{8}{{\sec }^{2}}45{}^\circ \]

\[=3{{\left( 1 \right)}^{2}}-{{\left( \frac{\sqrt{3}}{2} \right)}^{2}}-\frac{1}{3}{{\left( \sqrt{3} \right)}^{2}}-\frac{1}{8}{{\left( \sqrt{2} \right)}^{2}}\]

\[=3-\frac{3}{4}-\frac{1}{3}\times 3-\frac{1}{8}\times 2\]

\[=3-\frac{3}{4}-1-\frac{1}{4}\]

\[=\frac{12-3-4-1}{4}=\frac{12-8}{4}=\frac{4}{4}=1\]

∴ নির্নেয় মান = 1

(iv) \,\frac{4}{3}{{\cot }^{2}}30{}^\circ +3{{\sin }^{2}}60{}^\circ -2\cos e{{c}^{2}}60{}^\circ -\frac{3}{4}{{\tan }^{2}}30{}^\circ

উত্তর –

\[\frac{4}{3}{{\cot }^{2}}30{}^\circ +3{{\sin }^{2}}60{}^\circ -2\cos e{{c}^{2}}60{}^\circ -\frac{3}{4}{{\tan }^{2}}30{}^\circ \]

\[=\frac{4}{3}{{\left( \sqrt{3} \right)}^{2}}+3{{\left( \frac{\sqrt{3}}{2} \right)}^{2}}-2{{\left( \frac{2}{\sqrt{3}} \right)}^{2}}-\frac{3}{4}{{\left( \frac{1}{\sqrt{3}} \right)}^{2}}\]

\[=\frac{4}{3}\times 3+3\times \frac{3}{4}-2\times \frac{4}{3}-\frac{3}{4}\times \frac{1}{3}\]

\[=4+\frac{9}{4}-\frac{8}{3}-\frac{1}{4}\]

\[=\frac{48+27-32-3}{12}\]

\[=\frac{75-35}{12}=\frac{40}{12}=\frac{10}{3}=3\frac{1}{3}\]

∴ নির্নেয় মান = 3\frac{1}{3}

(v) \frac{\frac{1}{3}\cos 30{}^\circ }{\frac{1}{2}\sin 45{}^\circ }+\frac{\tan 60{}^\circ }{\cos 30{}^\circ }

উত্তর –

\[\frac{\frac{1}{3}\cos 30{}^\circ }{\frac{1}{2}\sin 45{}^\circ }+\frac{\tan 60{}^\circ }{\cos 30{}^\circ }\]

\[=\frac{\frac{1}{3}\times \frac{\sqrt{3}}{2}}{\frac{1}{2}\times \frac{1}{\sqrt{2}}}+\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}\]

\[=\frac{\sqrt{3}}{3\times 2}\times \frac{2\sqrt{2}}{1}+\sqrt{3}\times \frac{2}{\sqrt{3}}\]

\[=\frac{\sqrt{6}}{3}+2=\frac{\sqrt{6}+6}{3}\]

∴ নির্নেয় মান = \frac{\sqrt{6}+6}{3}

(vi) {{\cot }^{2}}30{}^\circ -2{{\cos }^{2}}60{}^\circ -\frac{3}{4}{{\sec }^{2}}45{}^\circ -4{{\sin }^{2}}30{}^\circ

উত্তর –

\[{{\cot }^{2}}30{}^\circ -2{{\cos }^{2}}60{}^\circ -\frac{3}{4}{{\sec }^{2}}45{}^\circ -4{{\sin }^{2}}30{}^\circ \]

\[={{\left( \sqrt{3} \right)}^{2}}-2{{\left( \frac{1}{2} \right)}^{2}}-\frac{3}{4}{{\left( \sqrt{2} \right)}^{2}}-4{{\left( \frac{1}{2} \right)}^{2}}\]

\[=3-2\times \frac{1}{4}-\frac{3}{4}\times 2-4\times \frac{1}{4}\]

\[=3-\frac{1}{2}-\frac{3}{2}-1\]

\[=\frac{6-1-3-2}{2}\]

\[=\frac{6-6}{2}=\frac{0}{2}=0\]

∴ নির্নেয় মান = 0

(vii) {{\sec }^{2}}60{}^\circ -{{\cot }^{2}}30{}^\circ -\frac{2\tan 30{}^\circ \cos ec60{}^\circ }{1+{{\tan }^{2}}30{}^\circ }

উত্তর –

\[{{\sec }^{2}}60{}^\circ -{{\cot }^{2}}30{}^\circ -\frac{2\tan 30{}^\circ \cos ec60{}^\circ }{1+{{\tan }^{2}}30{}^\circ }\]

\[={{\left( 2 \right)}^{2}}-{{\left( \sqrt{3} \right)}^{2}}-\frac{2\times \frac{1}{\sqrt{3}}\times \frac{2}{\sqrt{3}}}{1+{{\left( \frac{1}{\sqrt{3}} \right)}^{2}}}\]

\[=4-3-\frac{\frac{4}{3}}{1+\frac{1}{3}}\]

\[=1-\frac{\frac{4}{3}}{\frac{4}{3}}=1-1=0\]

∴ নির্নেয় মান = 0

(viii) \,\frac{\tan 60{}^\circ -\tan 30{}^\circ }{1+\tan 60{}^\circ \tan 30{}^\circ }+\cos 60{}^\circ \cos 30{}^\circ +\sin 60{}^\circ \sin 30{}^\circ

উত্তর –

\[\frac{\tan 60{}^\circ -\tan 30{}^\circ }{1+\tan 60{}^\circ \tan 30{}^\circ }+\cos 60{}^\circ \cos 30{}^\circ +\sin 60{}^\circ \sin 30{}^\circ \]

\[=\frac{\sqrt{3}-\frac{1}{\sqrt{3}}}{1+\sqrt{3}\times \frac{1}{\sqrt{3}}}+\frac{1}{2}\times \frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}\times \frac{1}{2}\]

\[=\frac{\frac{3-1}{\sqrt{3}}}{1+1}+\frac{\sqrt{3}}{4}+\frac{\sqrt{3}}{4}\]

\[=\frac{2}{\sqrt{3}}\times \frac{1}{2}+2\times \frac{\sqrt{3}}{4}\]

\[=\frac{1}{\sqrt{3}}+\frac{\sqrt{3}}{2}=\frac{2+3}{2\sqrt{3}}=\frac{5}{2\sqrt{3}}\]

∴ নির্নেয় মান =\frac{5}{2\sqrt{3}}

(ix) \,\frac{1-{{\sin }^{2}}30{}^\circ }{1+{{\sin }^{2}}45{}^\circ }\times \frac{{{\cos }^{2}}60{}^\circ +{{\cos }^{2}}30{}^\circ }{\cos e{{c}^{2}}90{}^\circ -{{\cot }^{2}}90{}^\circ }\div \left( \sin 60{}^\circ \tan 30{}^\circ  \right)

উত্তর –

\[\frac{1-{{\sin }^{2}}30{}^\circ }{1+{{\sin }^{2}}45{}^\circ }\times \frac{{{\cos }^{2}}60{}^\circ +{{\cos }^{2}}30{}^\circ }{\cos e{{c}^{2}}90{}^\circ -{{\cot }^{2}}90{}^\circ }\div \left( \sin 60{}^\circ \tan 30{}^\circ  \right)\]

\[=\frac{1-{{\left( \frac{1}{2} \right)}^{2}}}{1+{{\left( \frac{1}{\sqrt{2}} \right)}^{2}}}\times \frac{{{\left( \frac{1}{2} \right)}^{2}}+{{\left( \frac{\sqrt{3}}{2} \right)}^{2}}}{{{\left( 1 \right)}^{2}}-0}\div \left( \frac{\sqrt{3}}{2}\times \frac{1}{\sqrt{3}} \right)\]

\[=\frac{1-\frac{1}{4}}{1+\frac{1}{2}}\times \frac{\frac{1}{4}+\frac{3}{4}}{1}\div \frac{1}{2}\]

\[=\frac{\frac{3}{4}}{\frac{3}{2}}\times \frac{4}{4}\times 2=\frac{3}{4}\times \frac{2}{3}\times 1\times 2=1\]

∴ নির্নেয় মান = 1

6. দেখাই যে,

(i) \,{{\sin }^{2}}45{}^\circ +{{\cos }^{2}}45{}^\circ =1

উত্তর –

বামপক্ষ,

\[{{\sin }^{2}}45{}^\circ +{{\cos }^{2}}45{}^\circ \]

\[={{\left( \frac{1}{\sqrt{2}} \right)}^{2}}+{{\left( \frac{1}{\sqrt{2}} \right)}^{2}}\]

\[=\frac{1}{2}+\frac{1}{2}=1\]

∴ বামপক্ষ = ডানপক্ষ (প্রমানিত)।

(ii) \cos 60{}^\circ ={{\cos }^{2}}30{}^\circ -{{\sin }^{2}}30{}^\circ

উত্তর –

বামপক্ষ,

\[\cos 60{}^\circ =\frac{1}{2}\] 

ডানপক্ষ,

\[{{\cos }^{2}}30{}^\circ -{{\sin }^{2}}30{}^\circ \]

\[={{\left( \frac{\sqrt{3}}{2} \right)}^{2}}-{{\left( \frac{1}{2} \right)}^{2}}\]

\[=\frac{3}{4}-\frac{1}{4}\]

\[=\frac{3-1}{4}=\frac{2}{4}=\frac{1}{2}\]

∴ বামপক্ষ = ডানপক্ষ (প্রমানিত)।

(iii) \frac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }=\sqrt{3}

উত্তর –

বামপক্ষ,

\[\frac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }\]

\[=\frac{2\times \frac{1}{\sqrt{3}}}{1-{{\left( \frac{1}{\sqrt{3}} \right)}^{2}}}=\frac{\frac{2}{\sqrt{3}}}{1-\frac{1}{3}}=\frac{\frac{2}{\sqrt{3}}}{\frac{2}{3}}=\frac{2}{\sqrt{3}}\times \frac{3}{2}=\sqrt{3}\]

∴ বামপক্ষ = ডানপক্ষ (প্রমানিত)।

(iv) \sqrt{\frac{1+\cos 30{}^\circ }{1-\cos 30{}^\circ }}=\sec 60{}^\circ +\tan 60{}^\circ

উত্তর –

বামপক্ষ,

\[\sqrt{\frac{1+\cos 30{}^\circ }{1-\cos 30{}^\circ }}\]

\[=\sqrt{\frac{1+\frac{\sqrt{3}}{2}}{1-\frac{\sqrt{3}}{2}}}=\sqrt{\frac{\frac{2+\sqrt{3}}{2}}{\frac{2-\sqrt{3}}{2}}}=\sqrt{\frac{2+\sqrt{3}}{2-\sqrt{3}}}\]

\[=\sqrt{\frac{{{\left( 2+\sqrt{3} \right)}^{2}}}{\left( 2-\sqrt{3} \right)\left( 2+\sqrt{3} \right)}}=\sqrt{\frac{{{\left( 2+\sqrt{3} \right)}^{2}}}{4-3}}\]

\[=2+\sqrt{3}\]

ডানপক্ষ,

\[\sec 60{}^\circ +\tan 60{}^\circ =2+\sqrt{3}\]

∴ বামপক্ষ = ডানপক্ষ (প্রমানিত)।

(v) \frac{2{{\tan }^{2}}30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }+{{\sec }^{2}}45{}^\circ -{{\cot }^{2}}45{}^\circ =\sec 60{}^\circ

উত্তর –

বামপক্ষ,

\[\frac{2{{\tan }^{2}}30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }+{{\sec }^{2}}45{}^\circ -{{\cot }^{2}}45{}^\circ \]

\[=\frac{2{{\left( \frac{1}{\sqrt{3}} \right)}^{2}}}{1-{{\left( \frac{1}{\sqrt{3}} \right)}^{2}}}+{{\left( \sqrt{2} \right)}^{2}}-{{\left( 1 \right)}^{2}}\]

\[=\frac{2\times \frac{1}{3}}{1-\frac{1}{3}}+2-1=\frac{\frac{2}{3}}{\frac{2}{3}}+1\]

\[=1+1=2\]

ডানপক্ষ,

\[\sec 60{}^\circ =2\]

∴ বামপক্ষ = ডানপক্ষ (প্রমানিত)।

(vi) {{\tan }^{2}}\frac{\pi }{4}\sin \frac{\pi }{3}\tan \frac{\pi }{6}{{\tan }^{2}}\frac{\pi }{3}=1\frac{1}{2}

উত্তর –

বামপক্ষ,

\[{{\tan }^{2}}\frac{\pi }{4}\sin \frac{\pi }{3}\tan \frac{\pi }{6}{{\tan }^{2}}\frac{\pi }{3}\]

\[={{\left( 1 \right)}^{2}}\times \frac{\sqrt{3}}{2}\times \frac{1}{\sqrt{3}}\times {{\left( \sqrt{3} \right)}^{2}}\]

\[=1\times \frac{1}{2}\times 3=\frac{3}{2}=1\frac{1}{2}\]

∴ বামপক্ষ = ডানপক্ষ (প্রমানিত)।

(vii) \sin \frac{\pi }{3}\tan \frac{\pi }{6}+\sin \frac{\pi }{2}\cos \frac{\pi }{3}=2{{\sin }^{2}}\frac{\pi }{4}

উত্তর –

\[\sin \frac{\pi }{3}\tan \frac{\pi }{6}+\sin \frac{\pi }{2}\cos \frac{\pi }{3}\]

\[=\frac{\sqrt{3}}{2}\times \frac{1}{\sqrt{3}}+1\times \frac{1}{2}\]

\[=\frac{1}{2}+\frac{1}{2}=1\]

ডানপক্ষ,

\[2{{\sin }^{2}}\frac{\pi }{4}=2{{\left( \frac{1}{\sqrt{2}} \right)}^{2}}=2\times \frac{1}{2}=1\]

∴ বামপক্ষ = ডানপক্ষ (প্রমানিত)।

7. (i)  x\sin 45{}^\circ \cos 45{}^\circ \tan 60{}^\circ ={{\tan }^{2}}45{}^\circ -\cos 60{}^\circ হলে, x-এর মান নির্ণয় করি।

উত্তর –

\[x\sin 45{}^\circ \cos 45{}^\circ \tan 60{}^\circ ={{\tan }^{2}}45{}^\circ -\cos 60{}^\circ \]

\[\Rightarrow x\times \frac{1}{\sqrt{2}}\times \frac{1}{\sqrt{2}}\times \sqrt{3}={{\left( 1 \right)}^{2}}-\frac{1}{2}\]

\[\Rightarrow \frac{\sqrt{3}}{2}x=1-\frac{1}{2}\]

\[\Rightarrow \frac{\sqrt{3}}{2}x=\frac{1}{2}\]

\[\therefore \,\,x=\frac{1}{2}\times \frac{2}{\sqrt{3}}=\frac{1}{\sqrt{3}}\]

∴ নির্নেয় x-এর মান \frac{1}{\sqrt{3}}

(ii) x\sin 60{}^\circ {{\cos }^{2}}30{}^\circ =\frac{{{\tan }^{2}}45{}^\circ \sec 60{}^\circ }{\cos ec60{}^\circ } হলে, x-এর মান নির্ণয় করি।

উত্তর –

\[x\sin 60{}^\circ {{\cos }^{2}}30{}^\circ =\frac{{{\tan }^{2}}45{}^\circ \sec 60{}^\circ }{\cos ec60{}^\circ }\]

\[\Rightarrow x\left( \frac{\sqrt{3}}{2} \right){{\left( \frac{\sqrt{3}}{2} \right)}^{2}}=\frac{{{\left( 1 \right)}^{2}}\left( 2 \right)}{\left( \frac{2}{\sqrt{3}} \right)}\]

\[\Rightarrow x\times \frac{\sqrt{3}}{2}\times \frac{3}{4}=\frac{2\sqrt{3}}{2}\]

\[\Rightarrow x=\frac{2\sqrt{3}}{2}\times \frac{4}{3}\times \frac{2}{\sqrt{3}}\]

\[\therefore x=\frac{8}{3}=2\frac{2}{3}\]

∴ নির্নেয় x-এর মান 2\frac{2}{3}

(iii) {{x}^{2}}={{\sin }^{2}}30{}^\circ +4{{\cot }^{2}}45{}^\circ -{{\sec }^{2}}60{}^\circ হলে, x-এর মান নির্ণয় করি।

উত্তর –

\[{{x}^{2}}={{\sin }^{2}}30{}^\circ +4{{\cot }^{2}}45{}^\circ -{{\sec }^{2}}60{}^\circ \]

\[\Rightarrow {{x}^{2}}={{\left( \frac{1}{2} \right)}^{2}}+4{{\left( 1 \right)}^{2}}-{{\left( 2 \right)}^{2}}\]

\[\Rightarrow {{x}^{2}}=\frac{1}{4}+4-4\]

\[\Rightarrow {{x}^{2}}=\frac{1}{4}\]

\[\therefore \,x=\pm \sqrt{\frac{1}{4}}=\pm \frac{1}{2}\]

∴ নির্নেয় x-এর মান \pm \frac{1}{2}

8. x\tan 30{}^\circ +y\cot 60{}^\circ =0 এবং 2x-y\tan 45{}^\circ =1 হলে, x ও y-এর মান হিসাব করে লিখি।

উত্তর –

\[x\tan 30{}^\circ +y\cot 60{}^\circ =0\]

\[\Rightarrow x\times \frac{1}{\sqrt{3}}+y\times \frac{1}{\sqrt{3}}=0\]

\[\Rightarrow \frac{x}{\sqrt{3}}=-\frac{y}{\sqrt{3}}\]

\[\therefore \,\,x=-y.........\left( i \right)\]

আবার,

\[2x-y\tan 45{}^\circ =1\]

\[\Rightarrow 2\left( -y \right)-y\left( 1 \right)=1\]

\[\Rightarrow -2y-y=1\]

\[\Rightarrow -3y=1\]

\[\therefore \,\,y=-\frac{1}{3}\]

∴ (i) থেকে পাই,

\[x=-\left( -\frac{1}{3} \right)=\frac{1}{3}\]

∴ নির্নেয় x-এর মান \frac{1}{3}, y -এর মান -\frac{1}{3}

9. যদি A=B=45° হয়, তবে যাচাই করি যে,

(i) \sin \left( A+B \right)=\sin A\cos B+\cos A\sin B

(ii) \cos \left( A+B \right)=\cos A\cos B-\sin A\sin B

10. (i) ABC সমবাহু ত্রিভুজের BD একটি মধ্যমা। প্রমাণ করি যে, tan∠ABD=cot∠BAD

(ii) ABC সমদ্বিবাহু ত্রিভুজের AB=AC এবং ∠BAC=90°; ∠BAC-এর সমদ্বিখণ্ডক BC বাহুকে D বিন্দুতে ছেদ করে।

প্রমাণ করি যে, \frac{\sec \angle ACD}{\sin \angle CAD}=\cos e{{c}^{2}}\angle CAD

11. θ (0°≤θ≤90°)-এর কোন মান/মানগুলির জন্য 2{{\cos }^{2}}\theta -3\cos \theta +1=0 সত্য হবে নির্ণয় করি।

কষে দেখি - 23.3

1. (i) \sin \theta =\frac{4}{5} হলে, \frac{\cos ec\theta }{1+\cot \theta }-এর মান নির্ণয় করে লিখি। 

(ii) যদি \tan \theta =\frac{3}{4} হয়, তবে দেখাই যে  \sqrt{\frac{1-\sin \theta }{1+\sin \theta }}=\frac{1}{2}

(iii) \tan \theta =1 হলে,  \frac{8\sin \theta +5\cos \theta }{{{\sin }^{3}}\theta -2{{\cos }^{3}}\theta +7\cos \theta }-এর মান নির্ণয় করি।

2. (i) cosecθ এবং tanθ-কে sinθ-এর মাধ্যমে প্রকাশ করি।

(ii) cosecθ এবং tanθ-কে cosθ-এর মাধ্যমে লিখি।

3. (i) secθ + tanθ = 2 হলে, (secθ – tanθ)-এর মান নির্ণয় করি।

(ii) cosecθ – cotθ = \sqrt{2}-1 হলে, (cosecθ + cotθ)-এর মান হিসাব করে লিখি।

(iii) sinθ + cosθ = 1 হলে sinθ × cosθ-এর মান নির্ণয় করি।

(iv) tanθ + cotθ = 2 হলে, (tanθ – cotθ)-এর মান নির্ণয় করি।

(v) sinθ – cosθ = \frac{7}{13} হলে, sinθ + cosθ –এর মান নির্ণয় করি।

(vi) sinθcosθ = \frac{1}{2}হলে, (sinθ + cosθ) –এর মান হিসাব করে লিখি।

(vii) secθ – tanθ = \frac{1}{\sqrt{3}} হলে, secθ এবং tanθ উভয়ের মান নির্ণয় করি।

(viii) cosecθ + cotθ = \sqrt{3} হলে, cosecθ এবং cotθ উভয়ের মান নির্ণয় করি।

(ix) \frac{\sin \theta +\cos \theta }{\sin \theta -\cos \theta }=7 হলে, tanθ –এর মান হিসাব করে লিখি।

(x)  \frac{\cos ec\theta +\sin \theta }{\cos ec\theta -\sin \theta }=\frac{5}{2} হলে, sinθ–এর মান হিসাব করে লিখি।

(xi) secθ + cosθ = \frac{5}{2}হলে, ( secθ – cosθ) –এর মান হিসাব করে লিখি।

(xii) 5sin²θ + 4cos²θ = \frac{9}{2} সম্পর্কটি থেকে tanθ –এর মান নির্ণয় করি।

(xiii) tan2θ + cot2θ = \frac{10}{3}হলে,  tanθ + cotθ এবং tanθ – cotθ –এর মান নির্ণয় করি এবং সেখান থেকে tanθ –এর মান হিসাব করে লিখি।

(xiv) sec²θ + tan²θ = \frac{13}{4}হলে, (sec⁴θ – tan⁴θ) –এর মান হিসাব করে লিখি।

4. (i) PQR ত্রিভুজে ∠Q সমকোণ। PR = \sqrt{5} একক এবং PQ – RQ = 1 একক হলে, cosP – cosR –এর মান নির্ণয় করি।

(ii) XYZ ত্রিভুজে ∠Y সমকোণ। XY = 2\sqrt{3} একক এবং XZ – YZ = 2 একক হলে (secX – tanX)-এর মান নির্ণয় করি।

5. সম্পর্কগুলি থেকে ‘θ’ অপনয়ন করি -

(i) x = 2sin θ, y = 3cos θ             

(ii) 5x = 3sec θ, y=3tan θ

6. (i) যদি sinα = \frac{5}{13} হয়, তাহলে দেখাই যে tanα + secα = 1.5

(ii) যদি tanA = \frac{n}{m}হয়, তাহলে sinA ও secA উভয়ের মান নির্ণয় করি।

(iii) যদি cosθ = \frac{x}{\sqrt{{{x}^{2}}+{{y}^{2}}}} হয়, তাহলে দেখাই যে,  xsinθ = ycosθ

(iv) যদি sinα = \frac{{{a}^{2}}-{{b}^{2}}}{{{a}^{2}}+{{b}^{2}}} হয়, তাহলে দেখাই যে, cotα = \frac{2ab}{{{a}^{2}}-{{b}^{2}}}

(v) যদি \frac{\sin \theta }{x}=\frac{\cos \theta }{y} হয়, তাহলে দেখাই যে, \sin \theta -\cos \theta =\frac{x-y}{\sqrt{{{x}^{2}}+{{y}^{2}}}}

(vi) যদি (1 + 4x²)cosA = 4x হয়, তাহলে দেখাই যে, cosecA + cotA = \frac{1+2x}{1-2x}

7. যদি x = asinθ এবং y = btanθ হয়, তাহলে প্রমাণ করি যে, \frac{{{a}^{2}}}{{{x}^{2}}}-\frac{{{b}^{2}}}{{{y}^{2}}}=1

8. যদি sinθ + sin²θ = 1 হয়, তাহলে প্রমাণ করি যে, cos²θ + cos⁴θ = 1

9. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q)

(i) যদি 3x = cosecα এবং \frac{3}{x}=cotα হয়, তাহলে 3\left( {{x}^{2}}-\frac{1}{{{x}^{2}}} \right) -এর মান (a) \frac{1}{27}   (b) \frac{1}{81}   (c) \frac{1}{3}  (d) \frac{1}{9} 

(ii) যদি 2x = secA এবং \frac{2}{x}=\tan Aহয়, তাহলে 2\left( {{x}^{2}}-\frac{1}{{{x}^{2}}} \right) -এর মান (a) \frac{1}{2}   (b) \frac{1}{4}   (c) \frac{1}{8}  (d) \frac{1}{16}  

(iii) tanα + cotα = 2 হলে, (tan¹³α + cot¹³α)-এর মান  (a) 1  (b) 0  (c) 2  (d) কোনোটিই নয়

(iv) যদি sinθ – cosθ = 0 (0°≤θ≤90°) এবং secθ + cosecθ = x হয়, তাহলে x-এর মান (a) 1  (b) 2  (c) \sqrt{2}  (d) 2\sqrt{2}

(v) 2cos3θ = 1 হলে, θ-এর মান (a) 10°  (b) 15°  (c) 20°  (d) 30°  

(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি –

(i) যদি 0°≤α≤90° হয়, তাহলে (sec²α + cos²α)-এর সর্বনিম্ন মান 2

(ii) (cos0°×cos1°×cos2°×cos3°×…………cos90°)-এর মান 1

(C) শূন্যস্থান পূরণ করি –

(i) \left( \frac{4}{{{\sec }^{2}}\theta }+\frac{1}{1+{{\cot }^{2}}\theta }+3{{\sin }^{2}}\theta  \right)-এর মান __________

(ii) \sin \left( \theta -30{}^\circ  \right)=\frac{1}{2}হলে, cosθ-এর মান __________

(iii) cos2θ – sin2θ = \frac{1}{2} হলে, cos⁴θ – sin⁴θ-এর মান __________

10. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

(i) যদি r cosθ = 2\sqrt{3}, r sinθ = 2 এবং 0°<θ<90° হয়, তাহলে r এবং θ উভয়ের মান নির্ণয় করি।

(ii) যদি sinA + sinB = 2 হয়, যেখানে 0°≤A≤90° এবং 0°≤B≤90°, তাহলে (cosA + cosB)-এর মান নির্ণয় করি।

(iii) যদি 0°<θ<90° হয়, তাহলে (9tan²θ + 4cot²θ)-এর মান নির্ণয় করি।

(iv) (sin⁶α + cos⁶α + 3sin²αcos²α)-এর মান নির্ণয় করি।

(v) যদি cosec²θ = 2cotθ এবং 0°<θ<90° হয়, তাহলে θ-এর মান নির্ণয় করি।

;