অষ্টম শ্রেণি – তৃতীয় অধ্যায় : মূলদ সংখ্যার ধারণা সম্পূর্ণ সমাধান

মূলদ সংখ্যা

যে সংখ্যাকে \frac{p}{q} আকারে প্রকাশ করা যায়, যেখানে p এবং q পূর্ণসংখ্যা আর q\neq0 , তাদের মূলদ সংখ্যা বলে। তাই \frac23 এবং \frac{-7}6 হল মূলদ সংখ্যার উদাহরণ।

উদাহরণ

1. সকল ভগ্নাংশই হল মূলদ সংখ্যা। \frac83,\frac57এবং \frac{-47}6 হল কিছু মূলদ সংখ্যার উদাহরণ।
2. সকল স্বাভাবিক সংখ্যাই হল মূলদ সংখ্যা, কারন, 3=\frac21, 17=\frac{17}1
3. পূর্ণসংখ্যা 0, হল একটি মূলদ সংখ্যা, কারন, এটিকে \frac0{\pm1},\frac0{\pm2},\frac0{\pm3} ইত্যাদি আকারে প্রকাশ করা যায়।
4. সকল পূর্ণসংখ্যা হল একটি মূলদ সংখ্যা, কারন, 5=\frac51, -17=\frac{-17}1
5. সকল সমাপ্তি দশমিক হল মূলদ সংখ্যা। যেমন, 4.3=\frac{43}{10},0.\dot5=\frac59 ইত্যাদি।

ধনাত্মক মূলদ সংখ্যা

একটি মূলদ সংখ্যাকে তক্ষণই ধনাত্মক মূলদ সংখ্যা বলা হয় যদি এর লব এবং হর উভয় ধনাত্মক হয় বা উভয়ই  ঋনাত্মক হয়। যেমন, 3,\;\frac6{11} এবং \frac{-15}{-19} হল কিছু ধনাত্মক মূলদ সংখ্যা।

ঋনাত্মক মূলদ সংখ্যা

একটি মূলদ সংখ্যাকে তক্ষণই ঋনাত্মক মূলদ সংখ্যা বলা হয় যদি এর লব এবং হর এর মধ্যে যেকোনো একটি  ঋনাত্মক হয়। যেমন, -3,\;\frac6{-11} এবং \frac{-15}{19} হল কিছু ঋনাত্মক মূলদ সংখ্যা।

মূলদ সংখ্যার বৈশিষ্ট্য

১নং বৈশিষ্ট্য :- যদি \frac pq মূলদ সংখ্যা হয় এবং m একটি শূন্য নয় এমন পূর্ণসংখ্যা হয় তবে, \frac pq=\frac{p\times m}{q\times m}

সুতরাং, কোনও মূলদ সংখ্যার লব এবং হর উভয়কে শূন্য নয় এমন একটি পূর্ণসংখ্যা দিয়ে গুন করলে মূলদ সংখ্যাটি অপরিবর্তিত থাকে। উদাহরণ – \frac{-3}4=\frac{-3\times2}{4\times2}=\frac68=\frac{-3\times3}{4\times3}=\frac{-9}{12}=…

যদি কোনও মূলদ সংখ্যার হর ঋনাত্মক হয়, তাহলে এই বৈশিষ্ট্যের সাহায্যে লব ও হর উভয়কে দ্বারা গুন করে হরটিকে ধনাত্মক করা হয়। উদাহরণ – \frac2{-5}=\frac{2\times\left(-1\right)}{-5\times\left(-1\right)}=\frac{-2}5,\frac3{-5}=\frac{-3\times\left(-1\right)}{-5\times\left(-1\right)}=\frac35 ইত্যাদি।

২নং বৈশিষ্ট্য :- যদি \frac pq মূলদ সংখ্যা হয় এবং m  যদি p ও q  এর সাধারণ বিভাজক হয় তাহলে, \frac pq=\frac{p\div m}{q\div m}

সুতরাং, কোনও মূলদ সংখ্যার লব এবং হর উভয়কে শূন্য নয় এমন এর সাধারণ বিভাজক দিয়ে ভাগ করলে মূলদ সংখ্যাটি অপরিবর্তিত থাকে। উদাহরণ – \frac{-12}{18}=\frac{-12\div2}{18\div2}=\frac{-6}9=\frac{-12\div3}{18\div3}=\frac{-4}6 ইত্যাদি।

৩নং বৈশিষ্ট্য :– যদি দুটি মূলদ সংখ্যা \frac pq এবং \frac pq পরস্পর সমান হয় তবে, ps=qr \হবে।

অর্থাৎ, \frac pq=\frac rs\Rightarrow p\times s=q\times r

সমতুল্য মূলদ সংখ্যা

কোনও মূলদ সংখ্যার লব এবং হর উভয়কে শূন্য নয় এমন একটি পূর্ণসংখ্যা দিয়ে গুন অথবা ভাগ করলে আমরা সমতুল্য মূলদ সংখ্যা পাই। উদাহরণ –

\frac25=\frac{2\times2}{5\times2}=\frac4{10};\frac25=\frac{2\times3}{5\times3}=\frac6{15};\frac25=\frac{2\times4}{5\times4}=\frac8{20}; ইত্যাদি।

আবার, \frac{18}{30}=\frac{18\div2}{30\div2}=\frac9{15};\frac{18}{30}=\frac{18\div3}{30\div3}=\frac6{10};\frac{18}{30}=\frac{18\div6}{30\div6}=\frac35; ইত্যাদি।

সুতরাং, \frac25,\frac4{10},\frac6{15},\frac8{20}, ... ইত্যাদি সমতুল্য মূলদ সংখ্যা, একই রকমভাবে, \frac{18}{30},\frac9{15},\frac6{10},\frac35, ... ইত্যাদি সমতুল্য মূলদ সংখ্যা।

কষে দেখি – 3

1. নিচের সমীকরণগুলির সমাধান করি ও বীজগুলি  \frac pq[ (q\neq0) যেখানে p,q পূর্ণসংখ্যা ] আকারে প্রকাশ করি।

a) 7x=14          b) 4p+32=0     c) 11x=0          d) 5m-3=0       e) 9y+18=0         f)t=8-12t        

g) 6y=5+y       h) 2x+____=____           [নিজে মুলদ সংখ্যা বসাই]

উত্তরঃ-

\[a)7x=14\] \[\Rightarrow x=\frac{14}{7}\] \[\therefore x=2\]

\[b)4p+32=0\] \[\Rightarrow 4p=-32\] \[\Rightarrow p=\frac{-32}{4}\] \[\therefore p=-8\]

\[c)11x=0\] \[\Rightarrow x=\frac{0}{11}\] \[\therefore x=0\]

\[d)5m-3=0\] \[\Rightarrow 5m=3\] \[\therefore m=\frac{3}{5}\]

\[e)9y+18=0\] \[\Rightarrow 9y=-18\] \[\Rightarrow y=\frac{-18}{9}\] \[\therefore y=-2\]

\[f)t=8-12t\] \[\Rightarrow t+12t=8\] \[\Rightarrow 13t=8\] \[\therefore t=\frac{8}{13}\]

\[g)2x+7=10\] \[\Rightarrow 2x=10-7\] \[\Rightarrow 2x=3\] \[\therefore x=\frac{3}{2}\]

2.  y=-\frac54 হলে, -(-y)=y যাচাই করি।

উত্তরঃ-

\[-\left( -y \right)=-\left\{ -\left( -\frac{5}{4} \right) \right\}=-\left\{ \frac{5}{4} \right\}=-\frac{5}{4}=y\][প্রমানিত]

3. x=-\frac{3}{8} হলে, মান খুঁজি        a) 2x+5            b) x+\frac{3}{8}          c) 5-(-x)
d) ____ – (-x) [নিজে মুলদ সংখ্যা বসাই]।

উত্তরঃ-

\[x=-\frac{3}{8}\]

a)

\[2x+5=2(-\frac{3}{4})+5=-\frac{3}{4}+5=\frac{-3+20}{4}=\frac{17}{4}\]

b)

\[x+\frac{3}{8}=-\frac{3}{8}+\frac{3}{8}=0\]

c)

\[5-(-x)=5+x=5+(-\frac{3}{8})=5-\frac{3}{8}=\frac{40-3}{8}=\frac{37}{8}\]

d)

\[7-(-x)=7+x=7+(-\frac{3}{8})=7-\frac{3}{8}=\frac{56-3}{8}=\frac{53}{8}\]

4. নিচের ফাঁকা ঘরে বুঝে সংখ্যা লিখি :

a) \frac{9}{11}+\_\_\_=0       

b) \_\_\_+\left( -\frac{21}{29} \right)=0                          

c) \frac{7}{19}\times \_\_\_=1                 

d) -5\times \_\_\_=1

e) -\frac{15}{23}\times \_\_\_=1        

f) \left( -\frac{8}{3} \right)\times \left( -\frac{21}{20} \right)=\_\_\_

উত্তরঃ-

a) মনে করি অজানা সংখ্যাটি X

\begin{align}& \frac{9}{11}+x=0 \\& \Rightarrow x=0-\frac{9}{11} \\& \Rightarrow x=-\frac{9}{11} \\\end{align}

b) মনে করি অজানা সংখ্যাটি X

\begin{align}& x+(-\frac{21}{29})=0 \\& \Rightarrow x-\frac{21}{29}=0 \\& \Rightarrow x=0+\frac{21}{29} \\& \Rightarrow x=\frac{21}{29} \\\end{align}

c) \begin{align}& x\times \frac{7}{19}=1 \\& \Rightarrow x=\frac{1}{\frac{7}{19}} \\& \Rightarrow x=1\times \frac{7}{19} \\& \Rightarrow x=\frac{19}{7} \\\end{align}

d) \begin{align}& x\times (-5)=1 \\& \Rightarrow x=-\frac{1}{5} \\\end{align}

e) \begin{align}& -\frac{15}{23}\times x=1 \\& \Rightarrow x=\frac{1}{-\frac{15}{23}} \\& \Rightarrow x=1\times (-\frac{23}{15}) \\& \Rightarrow x=-\frac{23}{15} \\\end{align}

f) (-\frac{8}{3})\times (-\frac{21}{20})=\frac{14}{5}

5. \frac{7}{18} কে \left( -\frac{5}{6} \right) এর অনোন্যোক দিয়ে গুণ করে গুনফল লিখি।

উত্তরঃ-

(-5/6) এর অনন্যক (-6/5)

\[\therefore (\frac{7}{18})\times (-\frac{6}{5})=-\frac{7}{15}\]

6. বিনিময় ও সংযোগ নিয়মের সাহায্যে মান খুঁজি :

(i) \frac{5}{8}+\left( -\frac{7}{15} \right)+\left( \frac{3}{32} \right)+\frac{11}{75}        

(ii) \frac{8}{121}\times \frac{35}{169}\times \frac{55}{36}\times \frac{78}{49}

উত্তরঃ-

i)

\[\frac{5}{8}+\left( -\frac{7}{15} \right)+\left( \frac{3}{32} \right)+\frac{11}{75}\]

\[=\frac{5}{8}-\frac{7}{15}+\frac{3}{32}+\frac{11}{75}\]

\[=\left( \frac{5}{8}+\frac{3}{32} \right)+\left( \frac{11}{75}-\frac{7}{15} \right)\]

\[=\left( \frac{20+3}{32} \right)+\left( \frac{11-35}{75} \right)\]

\[=\frac{23}{32}+\left( -\frac{24}{75} \right)\]

\[=\frac{23}{32}-\frac{24}{75}\]

\[=\frac{1725-768}{2400}\]

\[=\frac{957}{2400}\]

\[=\frac{319}{800}\]

ii)

\[\frac{8}{121}\times \frac{35}{169}\times \frac{55}{36}\times \frac{78}{49}\]

\[=\frac{100}{3003}\]

7. সংখ্যারেখায় মুলদ সংখ্যাগুলি বসাই :              \frac{1}{4},-,\frac{3}{4},-,\frac{2}{3},\frac{6}{5},-,\frac{8}{3}

উত্তরঃ-

\frac{1}{4},-\frac{3}{4},-\frac{2}{3},\frac{6}{5},-\frac{8}{3}

\frac{1}{4}ও -\frac{3}{4} কে সংখ্যা রেখায় প্রকাশ করার জন্য পূর্ণসংখ্যার সংখ্যারেখার 0 থেকে 1 এবং 0 থেকে -1 এর মধ্যের দূরত্বকে সমান 4 ভাগে ভাগ করতে হবে।

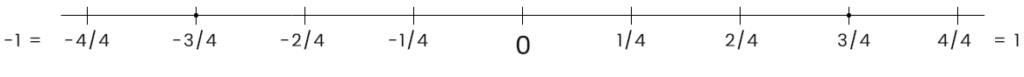
-\frac{2}{3}কে সংখ্যা রেখায় প্রকাশ করার জন্য পূর্ণসংখ্যার সংখ্যারেখার 0 থেকে -1 এর মধ্যের দূরত্বকে সমান 3 ভাগে ভাগ করতে হবে।

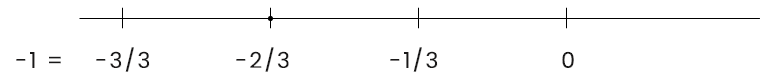
\frac{6}{5}=1\frac{1}{5} সংখ্যাটি 1 এর থেকে বড়, তাই সংখ্যাটিকে সংখ্যা রেখায় প্রকাশ করার জন্য পূর্ণসংখ্যার সংখ্যারেখার 1 থেকে 2 এর মধ্যের দূরত্বকে সমান 5 ভাগে ভাগ করতে হবে।

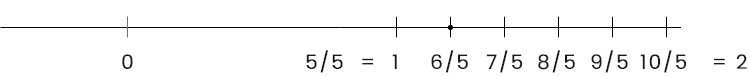
-\frac{8}{3}=-2\frac{2}{3} সংখ্যাটি -2 এর থেকে ছোট, তাই সংখ্যাটিকে সংখ্যা রেখায় প্রকাশ করার জন্য পূর্ণসংখ্যার সংখ্যারেখার -2 থেকে -3 এর মধ্যের দূরত্বকে সমান 3 ভাগে ভাগ করতে হবে।

8. 4টি মুলদ সংখ্যা লিখি যারা 1- এর থেকে বড় কিন্তু 2- এর থেকে ছোট।

উত্তরঃ-

1 এর থেকে বড় কিন্তু 2 এর থেকে ছোট চারটি মুলদ সংখ্যা হল- =\frac{7}{5},\frac{11}{7},\frac{7}{4},\frac{5}{3}

9. -\frac{3}{5} ও \frac{1}{2} এর মধ্যে 10টি মুলদ সংখ্যা খুঁজি :

[সংকেত:           -\frac{3}{5}=-\frac{6}{10}       ,              \frac{1}{2}=\frac{5}{10}]

উত্তরঃ-

-\frac{3}{5},\frac{1}{2} সংখ্যাদুটিকে সমহরে প্রকাশ করে পাই-

\[-\frac{3}{5}=\frac{-3\times 2}{5\times 2}=-\frac{6}{10}\]

\[\frac{1}{2}=\frac{1\times 5}{2\times 5}=\frac{5}{10}\]

এইবার সংখ্যারেখার প্রতিটি পূর্ণসংখ্যার মধ্যবর্তী দূরত্বকে 10টি সমান ভাগে ভাগ করে পাই।

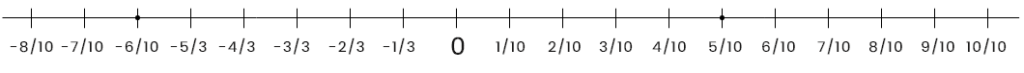
\therefore -\frac{3}{10}ও \frac{1}{2}এর মধ্যবর্তী 10টি মুলদ সংখ্যা হল

\[=-\frac{5}{10},-\frac{4}{10},-\frac{3}{10},-\frac{2}{10},-\frac{1}{10},0,\frac{1}{10},\frac{2}{10},\frac{3}{10},\frac{4}{10}\]

10. নিচের মুলদ সংখ্যাদুটির মধ্যে পাঁচটি করে মুলদ সংখ্যা লিখি :

a) \frac{1}{3}  ও \frac{3}{5}              

b) \frac{1}{4}  ও \frac{1}{2}              

c) -\frac{4}{3}  ও \frac{3}{7}

[সংকেত: হরগুলি সমান করে নিই, \frac{1}{3}=\frac{5}{15}=\frac{10}{30},\frac{3}{5}=\frac{9}{15}=\frac{18}{30}]

উত্তরঃ-

a)

\frac{1}{3}ও \frac{3}{5}কে সম হরে প্রকাশ করে পাই

\[\frac{1}{3}=\frac{1\times 5}{3\times 5}=\frac{5}{15}=\frac{5\times 2}{15\times 2}=\frac{10}{30}\]

\[\frac{3}{5}=\frac{3\times 3}{5\times 3}=\frac{9}{15}=\frac{9\times 2}{15\times 2}=\frac{18}{30}\]

\frac{1}{3}ও \frac{3}{5}এর মধ্যবর্তী 5টি মুলদ সংখ্যা হল

\[\frac{11}{30},\frac{12}{30},\frac{13}{30},\frac{14}{30},\frac{15}{30}\]

\[\frac{11}{30},\frac{2}{5},\frac{13}{30},\frac{7}{15},\frac{1}{2}\]

b)

\frac{1}{4}ও \frac{1}{2}কে সম হরে প্রকাশ করে পাই

\[\frac{1}{4}=\frac{1\times 1}{4\times 1}=\frac{1}{4}=\frac{1\times 6}{4\times 6}=\frac{6}{24}\]

\[\frac{1}{2}=\frac{1\times 2}{2\times 2}=\frac{2}{4}=\frac{2\times 6}{4\times 6}=\frac{12}{24}\]

\frac{1}{4}ও \frac{1}{2}এর মধ্যবর্তী 5টি মুলদ সংখ্যা হল

\[\frac{7}{24},\frac{8}{24},\frac{9}{24},\frac{10}{24},\frac{11}{24}\]

\[\frac{7}{24},\frac{1}{6},\frac{3}{8},\frac{5}{12},\frac{11}{24}\]

c)

-\frac{4}{3}ও \frac{3}{7}কে সমহরে প্রকাশ করে পাই

\[-\frac{4}{3}=\frac{-4\times 7}{3\times 7}=-\frac{28}{21}\]

\[\frac{3}{7}=\frac{3\times 3}{4\times 3}=\frac{9}{21}\]

-\frac{4}{3}ও \frac{3}{7}এর মধ্যবর্তী 5টি মুলদ সংখ্যা হল

\[-\frac{27}{21},-\frac{26}{21},-\frac{25}{21},-\frac{24}{21},-\frac{1}{1}\]

\[-\frac{9}{7},-\frac{26}{21},-\frac{25}{21},-\frac{8}{7},-1\]

;