কষে দেখি – 16.1
1. নীচের প্রতিক্ষেত্রে (x) এর মান লিখি।
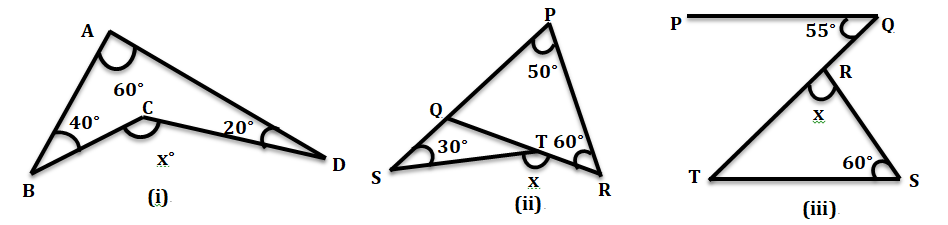
উত্তর-
(i) ∆ABE-এর বহিঃ ∠E = 40° + 60° = 100°
∆CDE-এর বহিঃ ∠C = x = 100° + 20° = 120°
(ii) ∠PQR = 180° – (50° + 60°) = 180° – 110° = 70°
∆QST-তে ∠PQR = ∠QST + ∠STQ
⟹ 70° = 30° + ∠STQ
∴ ∠STQ = 70° – 30° = 40°
∠QTR = সরলকোণ = 180°
∴ ∠STR = ∠QTR – ∠STQ = 180° – 40° = 140°
∴ x = ∠STR = 140°
(iii) ∠STQ = ∠PQT = 55° (∵ একান্তর কোণ)
∴ x = 180°- (∠S + ∠T) = 180° – (60° + 55°) = 180° – 115° = 65°
2. পাশের চিত্রে ∆EHG এর কোণগুলির পরিমাপ লিখি।
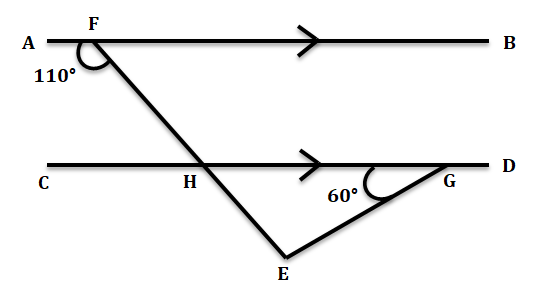
উত্তর-
∠AFG = 110° = ∠CHE [∵ AB||CD]
∆EHG ∠CHE = ∠HEG + ∠EGH [∵ ত্রিভুজের বহিঃস্থ কোণ বিপরীত অন্তঃস্থ কোণদ্বয়ের সমষ্টির সমান]
∴ 110° = ∠HEG + 60°
∴ ∠HEG = 110° – 60° = 50°
∴ ∠EHG = 180° – (50° + 60°) = 180° – 110° = 70°
∴ ∆EHG-এর কোণগুলি
∠EHG = 70° ও ∠HEG = 50°
3. পাশের চিত্রে ∠A + ∠B + ∠C + ∠D + ∠E + ∠F এর পরিমাপ লিখি।
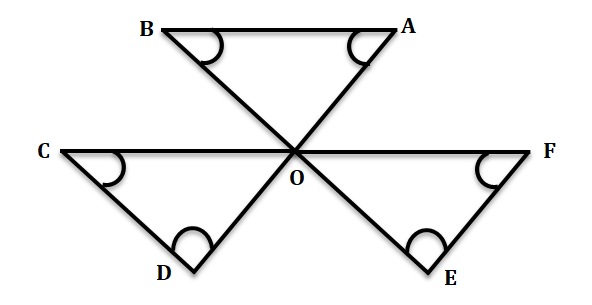
উত্তর-
∆AOB-তে ∠A + ∠B + ∠AOB = 180° ………….(i)
∆COD-তে ∠C + ∠D + ∠COD = 180° ………….(ii)
∆EOF-তে ∠F + ∠E + ∠EOF = 180° ………….(iii)
(i) + (ii) + (iii)করে পাই,
∠A + ∠B + ∠C + ∠D + ∠E + ∠F + ∠AOB + ∠COD + ∠EOF = 180° + 180° +180° = 540°
এখন, ∠AOB = ∠EOD [∵ বিপ্রতীপ কোণ ]
∠COD = ∠AOF [∵ বিপ্রতীপ কোণ ]
∠EOF = ∠COB [∵ বিপ্রতীপ কোণ ]
এবং যেহেতু ∠AOB + ∠EOD + ∠COD + ∠AOF + ∠EOF + ∠COB = 360°
∴ ∠AOB + ∠COD + ∠EOF = ½ × 360° = 180°
∴ ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = 540° – 180° = 360°
4. AB = AC হলে ∠ABC, ∠ACB ও ∠BAC –এর পরিমাপ লিখি।
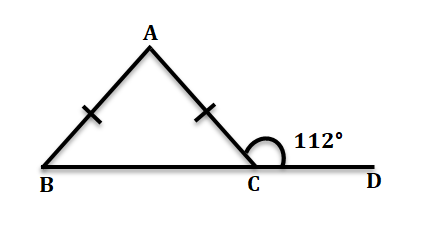
উত্তর-
∠BCD = ∠ACB + ∠ACD = 180°
⟹∠ACB + 112° = 180°
∴ ∠ACB = 180° – 112° = 68°
∵ AB = AC
∴ ∠ABC = ∠ACB = 68°
∴ ∠BAC = 180° – (68° + 68°) = 180° – 136° = 44°
∴ ∠ABC = 68°, ∠ACB = 68°, ∠BAC = 44°
5. AB = BC হলে ∠ABC ও ∠ACB –এর পরিমাপ লিখি।
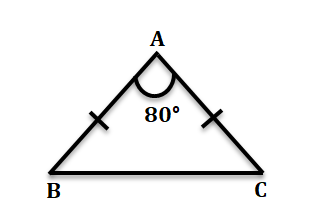
উত্তর-
∆ABC- তে
∵ AB = AC
∴ ∠ABC = ∠ACB
∠ABC + ∠ACB = 180° – 80° = 100°
∵ ∠ABC = ∠ACB
∴ ∠ABC = \frac{{{100}^{{}^\circ }}}{2}={{50}^{{}^\circ }} = ∠ACB
6. AB = BC হলে ∠ACB ও ∠BAC –এর পরিমাপ লিখি।
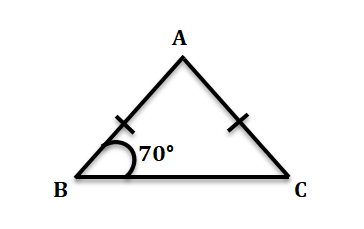
উত্তর-
∆ABC- তে
∵ AB = AC
∴ ∠ABC = ∠ACB = 70°
∴ ∠BAC = 180° – (70° + 70°) = 180° – 140° = 40°
7. AB = BC এবং ∠BAC + ∠ACB = 50°; ∆ABC-এর কোণগুলির পরিমাপ লিখি।
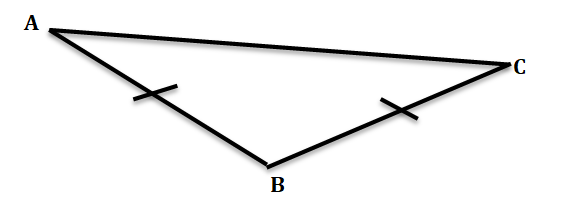
উত্তর-
∆ABC- তে
∵ AB = BC
∴ ∠BAC = ∠ACB
∵ ∠BAC + ∠ACB = 50°
∴ ∠BAC = ∠ACB = \frac{{{50}^{{}^\circ }}}{2}={{25}^{{}^\circ }}
এবং ∠ABC = 180° – 50° = 130°
∴ ∠ABC = 130°, ∠BAC = 25° ও ∠ACB = 25°
8. ∆ABC এর অন্তঃস্থ একটি বিন্দু O; প্রমাণ করি যে ∠BOC > ∠BAC
উত্তর-
Coming Soon…
9. প্রমাণ করি যে ∆ABC-এর BC বাহুকে উভয়দিকে বাড়ালে যে দুটি বহিঃকোণ উৎপন্ন হয় তাদের সমষ্টি 2 সমকোণের বেশি।
উত্তর-
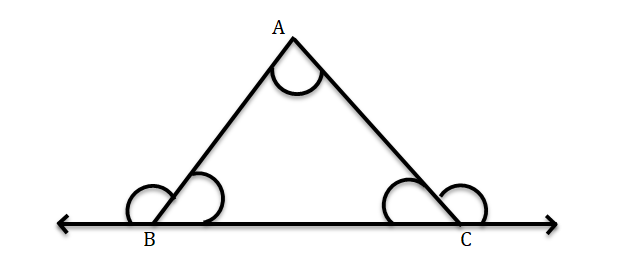
প্রদত্ত ∆ABC এর BC বাহুকে উভয়দিকে বৃদ্ধি করা হল।
প্রমাণ করতে হবে যে, বহিঃ ∠B + বহিঃ ∠C > 180° = 2 সমকোণ
প্রমাণ
বহিঃ ∠B = ∠BAC + ∠ACB বহিঃ ∠C = ∠BAC + ∠ABC
বহিঃ ∠B + বহিঃ ∠C = (∠BAC + ∠ACB) + (∠BAC + ∠ABC)
⟹ বহিঃ ∠B + বহিঃ ∠C = ∠BAC + (∠ACB + ∠BAC + ∠ABC)
⟹ বহিঃ ∠B + বহিঃ ∠C = ∠BAC + 180° [যেহেতু, একই ∆ABC এর তিনটি কোণ ]
∴ বহিঃ ∠B + বহিঃ ∠C > 180°
∴ বহিঃ ∠B + বহিঃ ∠C > 2 সমকোণ
10. ∆ABC এর কৌণিক বিন্দু A ও C দিয়ে যথাক্রমে BC ও BA বাহুর সমান্তরাল সরলরেখাংশ D বিন্দুতে মিলিত হয়। প্রমাণ করি যে, ∠ABC = ∠ADC
উত্তর-
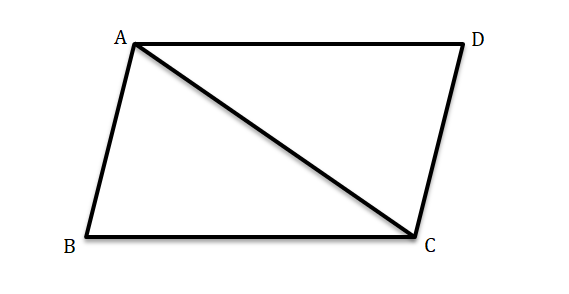
প্রদত্ত ∆ABC এর AB || CD এবং BC ||AD
প্রমাণ করতে হবে যে, ∠ABC = ∠ADC
প্রমাণ
∵ AB || CD এবং AD ছেদক
∴ ∠BAC = ∠ACD
আবার যেহেতু, BC ||AD এবং CD ছেদক
∴ ∠DAC = ∠ACB
এখন ∆ABC ও ∆ACD এর মধ্যে
∠BAC = ∠ACD, ∠DAC = ∠ACB এবং AC সাধারণ বাহু
∆ABC ≅ ∆ACD
∴ ∠ABC = ∠ADC (প্রমানিত)
11. ∆ABC এর ∠ABC ও ∠ACB এর অন্তঃসমদ্বিখন্ডকদ্বয় O বিন্দুতে মিলিত হয়। প্রমাণ করি যে, ∠BOC = 90° + ½ ∠BAC
উত্তর-
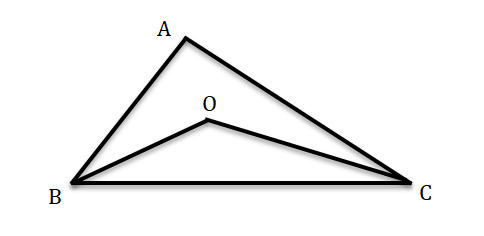
প্রদত্ত ∆ABC এর ∠ABC ও ∠ACB এর অন্তঃসমদ্বিখন্ডকদ্বয় O বিন্দুতে মিলিত হয়েছে।
প্রমাণ করতে হবে যে, ∠BOC = 90° + ½ ∠BAC
প্রমাণ
∆ABC এর
∠BAC + ∠ABC + ∠ACB = 180°
∴ ½∠BAC + ½∠ABC + ½∠ACB = ½(180°) = 90°
∴ ½∠ABC + ½∠ACB = 90° – ½∠BAC
আবার, ∆OBC এর
∠BOC + ∠OBC + ∠OCB = 180°
∴ ∠BOC = 180° – (∠OBC + ∠OCB)
⟹ ∠BOC = 180° – (½∠ABC + ½∠ACB)
⟹ ∠BOC = 180° – (90° – ½∠BAC)
⟹ ∠BOC = 180° – 90° + ½∠BAC
∴ ∠BOC = 90° + ½∠BAC (প্রমানিত)
12. ∆ABC এর ∠ABC ও ∠ACB এর বহিঃসমদ্বিখন্ডকদ্বয় O বিন্দুতে মিলিত হয়। প্রমাণ করি যে, ∠BOC = 90° + ½ ∠BAC
উত্তর-
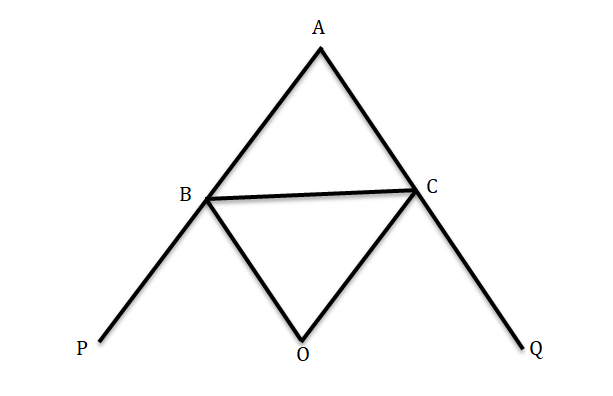
প্রদত্ত ∆ABC এর ∠ABC ও ∠ACB এর বহিঃসমদ্বিখন্ডকদ্বয় O বিন্দুতে মিলিত হয়েছে।
প্রমাণ করতে হবে যে, ∠BOC = 90° – ½ ∠BAC
প্রমাণ
∠ABC + ∠CBP = 180°
বা, ∠ABC + 2 ∠OBC = 180° [∵ BO, ∠CBP-কে সমদ্বিখন্ডিত করেছে]
বা, 2 ∠OBC = 180° – ∠ABC
বা, ∠OBC = ½ (180° – ∠ABC)
∴ ∠OBC = 90° – ½ ∠ABC
আবার, ∠ACB + ∠QCB = 180° [∵ সরলকোণ]
বা, ∠ACB + 2 ∠OCB = 180°
বা, 2 ∠OCB = 180° – ∠ACB
বা, ∠OCB = ½ (180° – ∠ACB)
∴ ∠OCB = 90° – ½ ∠ACB
∆BOC
∠OBC + ∠OCB + ∠BOC = 180° [ একই ত্রিভুজের তিনটি কোণ ]
বা, 90° – ½ ∠ABC + 90° – ½ ∠ACB + ∠BOC = 180°
বা, 180° – ½ (∠ABC + ∠ACB) + ∠BOC = 180°
বা, ∠BOC = ½ (∠ABC + ∠ACB)
বা, ∠BOC = ½(180° – ∠BAC) [∵∠ABC + ∠ACB + ∠BAC = 180° ]
∴ ∠BOC = 90° – ½ ∠BAC (প্রমানিত)
13. ∆ABC এর ∠ACB –এর বহিঃসমদ্বিখন্ডক A বিন্দু দিয়ে BC বাহুর সমান্তরাল সরলরেখাকে D বিন্দুতে ছেদ করে। প্রমাণ করি যে, ∠ADC = 90° – ½ ∠ACB
উত্তর-
Coming soon…
14. প্রমাণ করি যে, একটি ত্রিভুজের শীর্ষকোণের সমদ্বিখন্ডক এবং শীর্ষকোণ থেকে ভূমির উপর অঙ্কিত লম্বের অন্তর্ভুক্ত কোণ ত্রিভুজের ভূমিস্থ কোণদ্বয়ের অর্ধেক।
উত্তর-
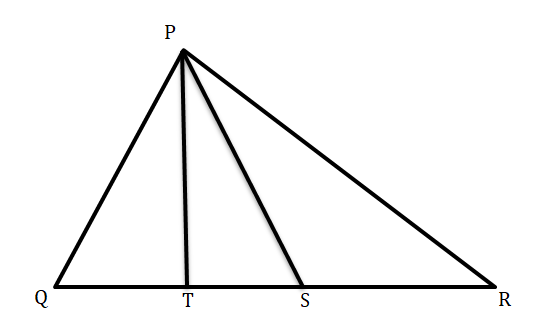
প্রদত্ত: ∆PQR এর শীর্ষকোণ P-এর সমদ্বিখণ্ডক PS এবং P থেকে ভূমি QR-এর উপর অঙ্কিত লম্ব PT
প্রমাণ করতে হবে যে, ∠TPS = ½ (∠PQR – ∠PRQ)
প্রমান
∵ PS, ∠QPR এর সমদ্বিখণ্ডক
∴∠QPS = ∠SPR ………(i)
∆PQT এর
∠PQT + ∠PTQ + ∠QPT = 180°
বা, ∠PQT + 90° + ∠QPT = 180°
বা, ∠PQT + ∠QPT = 90°
বা, ∠PQT = 90° – ∠QPT
∴ ∠PQR = 90° – ∠QPT ………(ii)
∆PTR এর
∠PRT + ∠TPR + ∠PTR = 180°
বা, ∠PRT + ∠TPR + 90° = 180°
বা, ∠PRT + ∠TPR = 90°
বা, ∠PRT = 90° – ∠TPR
∴ ∠PRQ = 90° – ∠TPR ………(iii)
(ii) – (iii) করে পাই,
∠PQR – ∠PRQ = (90° – ∠QPT) – (90° – ∠TPR)
বা, ∠PQR – ∠PRQ = ∠TPR – ∠QPT
বা, ∠PQR – ∠PRQ = (∠TPS + ∠SPR) – (∠QPS – ∠TPS)
বা, ∠PQR – ∠PRQ = 2∠TPS
∴ ∠TPS = ½ (∠PQR – ∠PRQ) (প্রমানিত)
15. ABC সমদ্বিবাহু ত্রিভুজের ভূমির একটি কোণ শীর্ষকোণের দ্বিগুন। ত্রিভুজটির কোণগুলির পরিমাপ লিখি।
উত্তর-
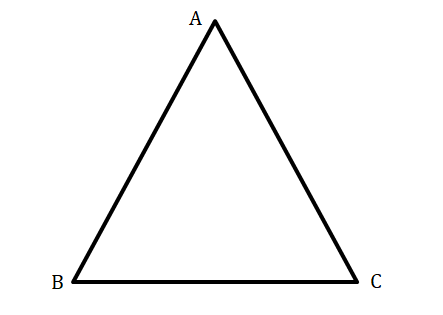
প্রদত্ত ABC একটি সমদ্বিবাহু ত্রিভুজ যার AB = AC, ∠ACB = 2∠BAC
∆ABC-এর কোণগুলির পরিমাপ নির্ণয় করতে হবে।
∠ABC = ∠ACB [∵ AB = AC]
∠BAC + ∠ABC + ∠ACB = 180° [∵ ত্রিভুজের তিনটি কোণের সমষ্টি 180°]
∠BAC + 2∠BAC + 2∠BAC = 180°
5∠BAC = 180°
∠BAC = 36°
∠ABC = 2 × 36° = 72°
∠ACB = 2 × 36° = 72°
16. ∆ABC-এর ∠BAC = 90° এবং ∠BCA = 30°; প্রমাণ করি যে, AB = ½ BC.
উত্তর-
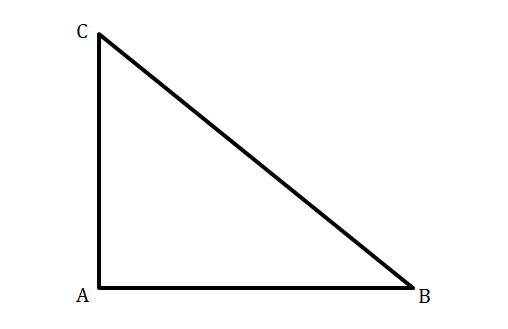
∆ABC-এর ∠BAC = 90° এবং ∠BCA = 30°
প্রমাণ করতে হবে যে, AB = ½ BC.
প্রমান
∆ABC-এর
∠ABC = 180° – (90° + 30°) = 180° – 120° = 60°
∠BCA = ½ ∠ABC
∠BCA এর বিপরীত বাহু AB এবং ∠ABC
∵ ত্রিভুজের কোণের সাথে তার বিপরীত বাহুগুলি সমানুপাতে থাকে
17. ∆XYZ-এর ∠XYZ = 90° এবং XY = XZ; প্রমাণ করি যে ∠YXZ = 60°
উত্তর-
Coming Soon…
18. প্রমাণ করি যে, সমবাহু ত্রিভুজের প্রতিটি কোণের পরিমাপ 60°
উত্তর-
Coming Soon…
19. ABC ত্রিভুজের ∠BAC-এর সমদ্বিখন্ডক এবং AC বাহুর মধ্যবিন্দু D দিয়ে AB বাহুর সমান্তরাল সরলরেখা পরস্পর BC বাহুর বাইরে E বিন্দুতে মিলিত হয়। প্রমাণ করি যে, ∠AEC = 1 সমকোণ।
উত্তর-
Coming Soon…
কষে দেখি – 16.2
Answers will come soon…
1. চিত্রে ∠QPR > ∠PQR, PR এবং QR বাহুর সম্পর্ক লিখি।
2. ∆ABCতে AC >AB. AC বাহুর D এমন একটি বিন্দু যে ∠ADB = ∠ABD; প্রমাণ করি ∠ABC > ∠ACB।
3. ABC ত্রিভুজে AB > AC; ∠BAC –এর সমদ্বিখন্ডক BC বাহুকে D বিন্দুতে ছেক করে। প্রমাণ করি যে, BD < CD।
4. ABC ত্রিভুজে AD, BC বাহুর উপর লম্ব এবং AC > AB; প্রমাণ করি যে, (i) ∠CAD > ∠BAD (ii) DC > BD
5. একটি চতুর্ভুজের বৃহত্তম ও ক্ষুদ্রতম বাহু দুটি বিপরীত। প্রমাণ করি যে, বৃহত্তম বাহুর সন্নিহিত একটি কোণ তাঁর বিপরীত কোণের চেয়ে ছোটো।
6. চিত্রে, AB < OB এবং CD > OD; প্রমাণ করি যে, ∠BAO > ∠OCD।
7. ∆PQR-এর PQ > PR; PQ বাহু থেকে PR বাহুর দৈর্ঘ্যের সমান করে PS সরলরেখাংশ কেটে নিলাম। R এবং S বিন্দু দুটি যুক্ত করলাম। প্রমাণ করি যে, (i) ∠PSR = ½ (∠PQR + ∠PRQ) (ii) ∠QRS = ½ (∠PRQ – ∠PQR)
8. ABC ত্রিভুজে, AB > AC; ∠BAC এর সমদ্বিখন্ডক BC বাহুকে D বিন্দুতে ছেদ করে। AB বাহু থেকে AC-এর দৈর্ঘ্যের সমান করে AE সরলরেখাংশ কেটে নিলাম। D, E যুক্ত করলাম। প্রমাণ করি যে, (i) ∆ACD ∆AED (ii) ∠ACB > ∠ABC
9. চিত্রে, AB = CD, ∠OCD > ∠COD এবং ∠OAB < ∠AOB প্রমাণ করি যে OB < OD
10. প্রমাণ করি যে, সমকোনী ত্রিভুজের অতিভুজ বৃহত্তম বাহু।
11. প্রমাণ করি যে, স্থুলকোনী ত্রিভুজে স্থুলকোণের বিপরীত বাহু বৃহত্তম। 12. ABC ত্রিভুজের ∠ABC ও ∠ACB এর সমদ্বিখন্ডকদ্বয় I বিন্দুতে মিলিত হয়। যদি AB > AC হয়, প্রমাণ করি যে, IB > IC
;

