Table of Contents
In the previous articles we studied, the tendency of data to cluster around a figure which is in the central location, in following articles we will study different measures of dispersion.
What is Dispersion?
Dispersion means scatteredness. So it is mean deviation or spread of values from their central values. It can also be defined as the difference between two extreme values of the series.
Requisites of Ideal Measures of Dispersion
The following are the requisites of ideal measure of dispersion:
It should be
1. Easy to understand and simple to calculate
2. Based on all values
3. Rigidly defined
4. Affected by extreme values
5. Affected by sampling fluctuations
6. Capable of further algebraic treatment
Types of Measures of Dispersion
There are two types of measures of variations
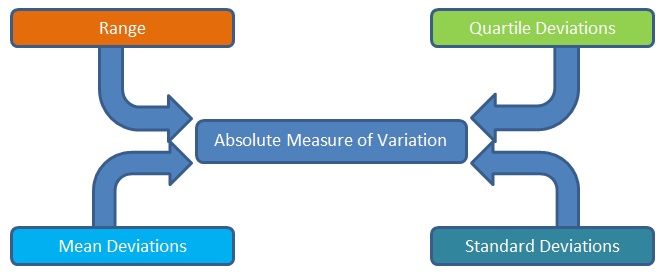
Absolute Measure of Variation
Under the absolute method, the dispersions are found out in the same unit in which data are expressed. But this method is not suitable for the comparative study of two or more distributions when the variables are expressed in different units.
It includes –
1. Range (R)
2. Quartile Deviations (Q.D.)
3. Mean Deviations (M.D.)
4. Standard Deviations (S.D.)
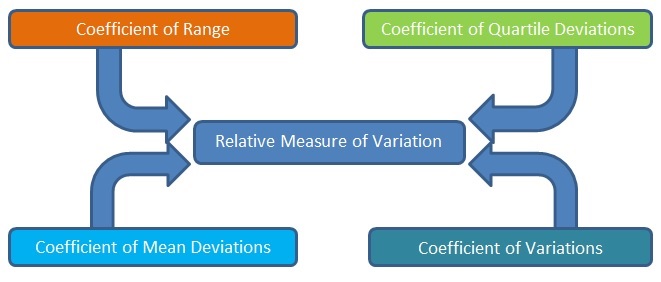
Relative Measure of Variation
The relative measure of variations is the ratio of a measure of absolute variation to an average. It is also known as the coefficient of variation. That is, it is a pure number that is independent of the unit of measurement.
It includes –
1. Coefficient of Range
2. Coefficient of Quartile Deviations
3. Coefficient of Mean Deviations
4. Coefficient of Variations
Mean Median Mode |
Standard Deviation |


