Functions in Group Theory with Examples

Functions

Let A and B be two non-empty sets. A function or a mapping f from A to be B is a rule which associates every element of A with a unique element of B and is denoted by f:A\to B .
In other words, a function f from A to B is a relation satisfying
i) Every element of A is related to some element of B.
ii) No element of A is related to two different elements of B.

Domain and Range of a Function

if f:A\to B is a function then A is called the domain and B is called the co-domain of f. If x\in A is associated with a unique element y\in B by the function f, then y is called the image of x under f and is denoted by y=f\left( x \right). Also, x is called the pre-image of y under f.

The range of f is the set of those elements of B which appear as the image of at least one element of A and is denoted by f\left( A \right). Thus f\left( A \right)=\left\{ f\left( x \right)\in B:x\in A \right\}. Clearly f\left( A \right) is a subset of B.

Example 01

Let A = {1, 2, 3, 4} and Z be the set of integers. Define f:A\to Z by f\left( x \right)=2x+3. Show that f is a function from A to B. Also find the range of f.

Solution:

Now,

\[f\left( 1 \right)=5,\,\,f\left( 2 \right)=7,\,\,f\left( 3 \right)=9,\,\,f\left( 4 \right)=11\]

\[\therefore f=\left\{ \left( 1,5 \right),\left( 2,7 \right),\left( 3,9 \right),\left( 4,11 \right) \right\}\]

Since every element of A is associated with a unique element of B, f is a function.
Therefore Range of f=\left\{ 5,7,9,11 \right\}

Example 02

Let N be the set of natural numbers. If f:N\to N is defined by f\left( x \right)=2x-1 show that f is a function and find the range of f.

Solution:

Now,

\[f\left( 1 \right)=1,\,f\left( 2 \right)=3,\,f\left( 3 \right)=5,\,….\]

\[\therefore f=\left\{ \left( 1,1 \right),\left( 2,3 \right),\left( 3,5 \right),\left( 4,7 \right),…. \right\}\]

Clearly, f is a function.
Therefore, Range of f=\left\{ 1,3,5,7,.... \right\}

Example 03

Let R be the set of real numbers. Defined f:R\to R\,\,by\,\,f\left( x \right)={{x}^{2}} for every x\in R. Show that f is a function and find the range of f.

Solution:

Here f associates every real number to its square, which is certainly a real number. Hence f is a function. Range of R is the set of all non-negative real numbers.

One-One Function or Injection

A function f:A\to B is said to be one-one or injection if for all {{x}_{1}},\,{{x}_{2}}\in A,\,f\left( {{x}_{1}} \right)=f\left( {{x}_{2}} \right)\,\,implies\,\,{{x}_{1}}={{x}_{2}}. The contrapositive of this implication is that of all {{x}_{1}},\,{{x}_{2}}\in A,\,{{x}_{1}}\ne {{x}_{2}}\,\,implies\,\,f\left( {{x}_{1}} \right)\ne f\left( {{x}_{2}} \right)\,.

Thus a function f:A\to B is said to be one-one if different elements of A have different images in B.

Example 04

Let R be the set of real numbers. Defined f:R\to R\,\,by\,\,i)f\left( x \right)=2x+3\,\,ii)f\left( x \right)={{x}^{3}} for every x\in R. Prove that f is one-one.

Solution:

i) Let f\left( {{x}_{1}} \right)=f\left( {{x}_{2}} \right) for some {{x}_{1}},\,{{x}_{2}}\in R

\[\Rightarrow 2{{x}_{1}}+3=2{{x}_{2}}+3\]

\[\Rightarrow {{x}_{1}}={{x}_{2}}\]

Thus for every {{x}_{1}},\,{{x}_{2}}\in R,\,f\left( {{x}_{1}} \right)=f\left( {{x}_{2}} \right)\,\,implies\,\,{{x}_{1}}={{x}_{2}}. Therefore f is one-one.

ii) Let f\left( {{x}_{1}} \right)=f\left( {{x}_{2}} \right) for some {{x}_{1}},\,{{x}_{2}}\in R

\[\Rightarrow {{x}_{1}}^{3}={{x}_{2}}^{3}\]

\[\Rightarrow {{x}_{1}}={{x}_{2}}\]

Thus for every {{x}_{1}},\,{{x}_{2}}\in R,\,f\left( {{x}_{1}} \right)=f\left( {{x}_{2}} \right)\,\,implies\,\,{{x}_{1}}={{x}_{2}}. Therefore f is one-one.

Example 05

If f:R\to R is defined by f\left( x \right)={{x}^{2}} for every x\in R , show that f is not one-one.

Solution:

Let

\[f\left( {{x}_{1}} \right)=f\left( {{x}_{2}} \right)\]

\[\Rightarrow {{x}_{1}}^{2}={{x}_{2}}^{2}\]

\[\Rightarrow {{x}_{1}}=\pm {{x}_{2}}\]

Hence f is not one-one.
For example, f\left( -2 \right)=4\,\,and\,\,f\left( 2 \right)=4. The images of -2 and 2 are not different. Hence f is not one-one.

Onto Function or Surjection

A function f:A\to B is said to be onto or surjection if for every y\in B there exist at least one element x\in A such that f\left( x \right)=y i.e., every element of the co-domain B appears as the image of at least one element of the domain A.

If f is onto, then f\left( A \right)=B.

Example 06

Defined f:R\to R\,\,by\,\,i)f\left( x \right)=2x+3\,\,ii)f\left( x \right)={{x}^{3}} for every x\in R. Show that f is onto.

Solution:

i) Let y\in R then to find x\in R such that f\left( x \right)=y\,\,i.e.,\,2x+3=y
Solving for x we get, x=\frac{y-3}{2}
Since y\in R,\,x=\frac{y-3}{2}\in R
Hence for every y\in R\,\,exists\,\,x=\frac{y-3}{2}\in Rsuch that f\left( \frac{y-3}{2} \right)=y. Therefore f is onto.

ii) Let y\in R.
We shall show that there exists x\in Rsuch that f\left( x \right)=y.
That is {{x}^{3}}=y.
Hence x={{y}^{\frac{1}{3}}}. If y\in R,\,\,then\,\,{{y}^{\frac{1}{3}}}\in R.
Thus for every y\in R there exists {{y}^{\frac{1}{3}}}\in R such that f\left( {{y}^{\frac{1}{3}}} \right)={{\left( {{y}^{\frac{1}{3}}} \right)}^{3}}=y.
Therefore f is onto.

Example 07

If f:R\to R is defined by f\left( x \right)={{x}^{2}} for every x\in R then prove that f is not onto.

Solution:

Since a negative number is the square of any real number, the negative numbers do not appear as the image of any element of R. For example, -9\in R but there does not exist any x\in R such that f\left( x \right)={{x}^{2}}=-9. Hence f is not onto.

One-to-one function or Bijection

A function f:A\to B is said to be one-to-one or bijection if it is both one-one and onto.
For example, if f:R\to R is defined by i)f\left( x \right)=2x+3\,\,ii)f\left( x \right)={{x}^{3}} for every x\in R then f is one-to-one function.

Inverse Image of an element

Let f:A\to B be a function and y\in B. Then the inverse image of y under f denoted by {{f}^{-1}}\left( y \right) is the set of those elements of A which have y as their image.

That is {{f}^{-1}}\left( y \right)=\left\{ x\in A:f\left( x \right)=y \right\}.

Example 08

If f:R\to R\, is defined by f\left( x \right)={{x}^{2}}-3x+5 find \left( i \right)\,{{f}^{-1}}\left( 3 \right)\,\,and\,\,\left( ii \right)\,{{f}^{-1}}\left( 15 \right)

Solution:

i) Let

\[{{f}^{-1}}\left( 3 \right)\,=y\Rightarrow f\left( y \right)=3\]

\[\Rightarrow {{y}^{2}}-3y+5=3\]

\[\Rightarrow {{y}^{2}}-3y+2=0\]

\[\Rightarrow \left( y-1 \right)\left( y-2 \right)=0\]

\[\therefore \,y=1\,\,or\,\,y=2\]

Therefore, {{f}^{-1}}\left( 3 \right)\,=\left\{ 1,\,2 \right\}

ii) Let

\[{{f}^{-1}}\left( 15 \right)=y\Rightarrow f\left( y \right)=15\]

\[\Rightarrow {{y}^{2}}-3y+5=15\]

\[\Rightarrow {{y}^{2}}-3y-10=0\]

\[\Rightarrow \left( y-5 \right)\left( y+2 \right)=0\]

\[\therefore \,y=5\,\,or\,\,y=-2\]

Hence, {{f}^{-1}}\left( 15 \right)=\left\{ -2,\,5 \right\}

Inverse Function

If a function f:A\to B is one-one and onto then the inverse of f denoted by {{f}^{-1}}:B\to A is denoted by {{f}^{-1}}=\left\{ \left( y,x \right):\left( x,y \right)\in f \right\}

Thus if f:A\to B is both one-one and onto then {{f}^{-1}}:B\to A is obtained by reversing the ordered pairs of f.

Note: {{f}^{-1}} exists only when f is both one-one and onto. Further {{f}^{-1}} is also one-one and onto.

Example 09

Let Q be the set of the rational numbers. If f:Q\to Q is defined by f\left( x \right)=2x-3 for every x\in Q then find {{f}^{-1}} if it exists.

Solution:

i) Let

\[f\left( {{x}_{1}} \right)=f\left( {{x}_{1}} \right)\]

\[\Rightarrow 2{{x}_{1}}-3=2{{x}_{2}}-3\]

\[\Rightarrow {{x}_{1}}={{x}_{2}}\]

Hence f is one-one.

ii) Let y\in Q. Then to find x\in Q:f\left( x \right)=y
i.e., 2x-3=y therefore x=\frac{y+3}{2}
Whenever y is rational, x=\frac{y+3}{2} is also a rational. Hence there exists \frac{y+3}{2}\in Q such that f\left( \frac{y+3}{2} \right)=y
Hence f is also onto. Therefore {{f}^{-1}}:Q\to Q exists.

Let x={{f}^{-1}}\left( y \right)\Rightarrow f\left( x \right)=y
i.e., 2x-3=ytherefore x=\frac{y+3}{2}
Define {{f}^{-1}}:Q\to Q\,\,by\,\,{{f}^{-1}}\left( y \right)=\frac{y+3}{2} for every y\in Q.
Replacing y by x we get {{f}^{-1}}\left( x \right)=\frac{x+3}{2},\,\,x\in Q. This is the required inverse function.

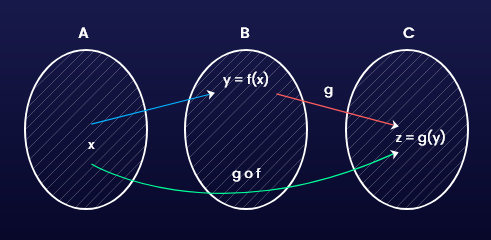
Composite Function or Product Function

If f:A\to Band g:B\to Care two functions then the composite function of f and g is denoted by gofis a function from A to C defined by \left( gof \right)\left( x \right)=g\left\{ f\left( x \right) \right\} for every x\in A
Here \left( gof \right)\left( x \right)=g\left\{ f\left( x \right) \right\}=g\left\{ y \right\}=z

Note: gof\ne fog. That is composition of mapping is not commutative.

Example 10

Let R be the set of real numbers. Define f:R\to R\,\,and\,\,g:R\to R\,\,by\,\,f\left( x \right)=3x-2\,\,and\,\,g\left( x \right)={{x}^{2}}+4 find (i) gof (ii) fog

Solution:

\[(i) \left( gof \right)\left( x \right)=g\left\{ f\left( x \right) \right\}=g\left\{ 3x-2 \right\}={{\left( 3x-2 \right)}^{2}}+4=9{{x}^{2}}-12x+8\,\,\forall x\in R\]

\[(ii) \left( fog \right)\left( x \right)=f\left\{ g\left( x \right) \right\}=f\left\{ {{x}^{2}}+4 \right\}=3\left( {{x}^{2}}+4 \right)-2=3{{x}^{2}}+10\,\forall x\in R\]

Example 11

If f\left( x \right)=\frac{1}{1-x},\,x\ne 1 find f\left[ f\left\{ f\left( x \right) \right\} \right]

Solution:

Now,

\[f\left[ f\left\{ f\left( x \right) \right\} \right]\]

\[=f\left[ f\left\{ \frac{1}{1-x} \right\} \right]=f\left[ \frac{1}{1-\frac{1}{1-x}} \right]=f\left[ \frac{1-x}{1-x-1} \right]=f\left[ \frac{1-x}{-x} \right]=f\left[ \frac{x-1}{x} \right]\]

\[\therefore f\left[ f\left\{ f\left( x \right) \right\} \right]=\frac{1}{1-\frac{x-1}{x}}=\frac{x}{x-x+1}=x\]

<< Previous Topic Relations

Next Topic >> Sequences

;