Definition of Circle
If a point is moving in a plane at equal distances from a fixed point, its path of transmission or locus is called a circle. The fixed point is called the center of the circle and the fixed distance from the moving fixed point is called the radius of the circle.
Some Formulae on Circle
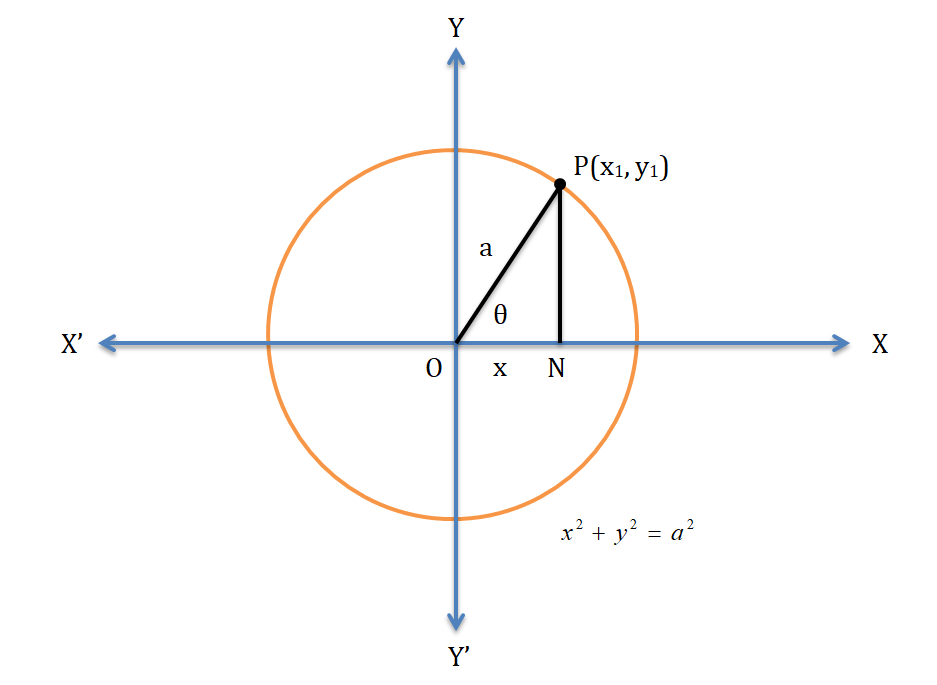
1. The equation of a circle having center at origin and radius ‘a’ is {{x}^{2}}+{{y}^{2}}={{a}^{2}}.........\left( 1 \right)
The parametric equation of the circle (1) is
\[x=a\cos \theta ,\,\,y=a\sin \theta \]
2. The equation of a circle with center at (α, β) and radius ‘a’ is
\[{{\left( x-\alpha \right)}^{2}}+{{\left( y-\beta \right)}^{2}}={{a}^{2}}\]
3. The general equation of a circle is {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 with center at \left( -g,-f \right) and radius = \sqrt{{{g}^{2}}+{{f}^{2}}-c}.
The circle makes x-intercept of 2\sqrt{{{g}^{2}}-c} unit and y-intercept of 2\sqrt{{{f}^{2}}-c} unit.
4. The quadratic equation a{{x}^{2}}+2hxy+b{{y}^{2}}+2gx+2fy+c=0 will represent the equation of a circle if a = b and h = 0.
5. If (x1, y1) and (x2, y2) be the end points of diameter of circle then the equation of the circle is \[\left( x-{{x}_{1}} \right)\left( x-{{x}_{2}} \right)+\left( y-{{y}_{1}} \right)\left( y-{{y}_{2}} \right)=0\]
6. Equation of the circle passing through the intersecting points of the circles {{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+2{{f}_{1}}y+{{c}_{1}}=0 and {{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+2{{f}_{1}}y+c\,=\,0, {{x}^{2}}+{{y}^{2}}+2{{g}_{2}}x+2{{f}_{2}}y+{{c}_{2}}=0 is \[{{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+2{{f}_{1}}y+{{c}_{1}}+k\left( {{x}^{2}}+{{y}^{2}}+2{{g}_{2}}x+2{{f}_{2}}y+{{c}_{2}} \right)=0\,\,\left[ k\ne 0 \right]\]
7. Equation of the concentric circle with the circle {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 is \[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c’=0\]
8. The point (x1, y1) will be in, on or outer of the circle {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0 if \[{{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+2{{f}_{1}}y+c>0,\,\,=\,\,or\,\,<0\]
9. Equation of the common chord of the circles {{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+2{{f}_{1}}y+c\,=\,0 and {{x}^{2}}+{{y}^{2}}+2{{g}_{1}}x+2{{f}_{1}}y+c\,=\,0 is \[2\left( {{g}_{1}}-{{g}_{2}} \right)x+2\left( {{f}_{1}}-{{f}_{2}} \right)y+{{c}_{1}}-{{c}_{2}}=0\]
| Example 01 |
A circle passes through the point (5, –1) and its center is at (2, –3). Find the equation of the circle.
Solution:
The circle passes through the point (5, –1) and its center is at (2, –3). So its radius = \sqrt{{{\left( 5-2 \right)}^{2}}+{{\left( -1+3 \right)}^{2}}}=\sqrt{9+4}=\sqrt{13}
Therefore the equation of the circle is
\[{{\left( x-2 \right)}^{2}}+{{\left( y+3 \right)}^{2}}={{\left( \sqrt{13} \right)}^{2}}\]
\[\Rightarrow {{x}^{2}}-4x+4+{{y}^{2}}+6y+9=13\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-4x+6y=0\]
| Example 02 |
Find the center and radius of the circle 5{{x}^{2}}+5{{y}^{2}}-8x+6y-15=0.
Solution:
We have,
\[5{{x}^{2}}+5{{y}^{2}}-8x+6y-15=0\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-\frac{8}{5}x+\frac{6}{5}y-3=0\]
Comparing it with the general form of the circle {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0, we get
\[2g=-\frac{8}{5};\,\,2f=\frac{6}{5}\,\,and\,\,c=-3\]
\[\Rightarrow g=-\frac{4}{5};\,\,f=\frac{3}{5}\,\,and\,\,c=-3\]
So, the center of the circle is \left( -g,-f \right)=\left( \frac{4}{5},-\frac{3}{5} \right) and radius = \sqrt{{{g}^{2}}+{{f}^{2}}-c}=\sqrt{{{\left( -\frac{4}{5} \right)}^{2}}+{{\left( \frac{3}{5} \right)}^{2}}-\left( -3 \right)}=\sqrt{4}=2 units
| Example 03 |
Find the parametric equation of the circle {{x}^{2}}+{{y}^{2}}-5x+2y+5=0.
Solution:
We have,
\[{{x}^{2}}+{{y}^{2}}-5x+2y+5=0\]
\[\Rightarrow {{x}^{2}}-2\times x\times \frac{5}{2}+{{\left( \frac{5}{2} \right)}^{2}}+{{y}^{2}}+2\times y\times 1+{{\left( 1 \right)}^{2}}={{\left( \frac{5}{2} \right)}^{2}}+{{\left( 1 \right)}^{2}}-5\]
\[\Rightarrow {{\left( x-\frac{5}{2} \right)}^{2}}+{{\left( y+1 \right)}^{2}}=\frac{9}{4}\]
\[\Rightarrow {{\left( x-\frac{5}{2} \right)}^{2}}+{{\left( y+1 \right)}^{2}}={{\left( \frac{3}{2} \right)}^{2}}\]
Obviously, x-\frac{5}{2}=\frac{3}{2}\cos \theta \,\,and\,\,y+1=\frac{3}{2}\sin \theta satisfies the above equation.
Therefore, the parametric equation of the given circle is
\[x-\frac{5}{2}=\frac{3}{2}\cos \theta \,\,and\,\,y+1=\frac{3}{2}\sin \theta \]
\[\Rightarrow x=\frac{1}{2}\left( 5+3\cos \theta \right)\,\,and\,\,y=-1+\frac{3}{2}\sin \theta \]
| Example 04 |
If 2{{x}^{2}}+2{{y}^{2}}+3x-y-5=0 be the inner circle of an equilateral triangle, then find the area of the triangle.
Solution:
We have
\[2{{x}^{2}}+2{{y}^{2}}+3x-y-5=0\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}+\frac{3}{2}x-\frac{1}{2}y-\frac{5}{2}=0\]
Therefore radius of the above circle r = \sqrt{{{\left( \frac{3}{4} \right)}^{2}}+{{\left( -\frac{1}{4} \right)}^{2}}-\left( -\frac{5}{2} \right)}=\sqrt{\frac{9}{16}+\frac{1}{16}+\frac{5}{2}}=\frac{1}{4}\sqrt{50} units
Now, let each side of the equilateral triangle be ‘a’ and area be △, then
\[\Delta =\frac{\sqrt{3}}{4}{{a}^{2}}\,\,and\,\,\Delta =rs=r\times \frac{3a}{2}\,\,\left[ \because s=Half\,of\,perimeter=\frac{3a}{2} \right]\]
\[\therefore \frac{\sqrt{3}}{4}{{a}^{2}}=r\times \frac{3a}{2}\]
\[\Rightarrow a=2\sqrt{3}r\]
\[\therefore \Delta =\frac{\sqrt{3}}{4}{{a}^{2}}=\frac{\sqrt{3}}{4}{{\left( 2\sqrt{3}r \right)}^{2}}=\frac{\sqrt{3}}{4}\times 12{{r}^{2}}\]
\[=3\sqrt{3}\times \frac{50}{16}\,\,\left[ \because \,r=\frac{1}{4}\sqrt{50} \right]\]
\[=\frac{75\sqrt{3}}{8}\]
Therefore, area of the equilateral triangle is \frac{75\sqrt{3}}{8} sq. units.
| Example 05 |
The center of a circle lies on the straight line 3x-2y+8=0 and passes through the points (2, 3) and (–6, –1). Find the equation of the circle.
Solution:
Let the equation of the circle be
\[{{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0………\left( 1 \right)\]
Since, (1) passes through the points (2, 3) and (–6, –1)
\[{{\left( 2 \right)}^{2}}+{{\left( 3 \right)}^{2}}+2g\left( 2 \right)+2f\left( 3 \right)+c=0\]
\[\Rightarrow 4+9+4g+6f+c=0\]
\[\Rightarrow 4g+6f+c+13=0………\left( 2 \right)\]
\[{{\left( -6 \right)}^{2}}+{{\left( -1 \right)}^{2}}+2g\left( -6 \right)+2f\left( -1 \right)+c=0\]
\[\Rightarrow 36+1-12g-2f+c=0\]
\[\Rightarrow -12g-2ff+c+37=0………\left( 3 \right)\]
Again the center \left( -g,-f \right) of the given circle lies on the straight line 3x-2y+8=0
\[\therefore 3\left( -g \right)-2\left( -f \right)+8=0\]
\[\Rightarrow -3g+2f+8=0……….\left( 4 \right)\]
Now subtracting (3) from (2) we get,
\[16g+8f-24=0\]
\[\Rightarrow 2g+f-3=0………….\left( 5 \right)\]
Solving (4) and (5) we get, g=2,\,\,f=-1
Putting the values of g\,and\,f in (2) we get, c = –15
Therefore, required equation of the circle is
\[{{x}^{2}}+{{y}^{2}}+4x-2y-15=0\]
| Example 06 |
If a circle touches the x-axis at the origin and passes through the point (h, k), find the equation of the circle.
Solution:
Since the circle touches the x-axis at the origin, so the ordinate of the center of the circle is equal to the radius of the circle.
Let the radius of the circle = a and coordinate of the center is (α, a). Then the equation of the circle will be
\[{{\left( x-\alpha \right)}^{2}}+{{\left( y-a \right)}^{2}}={{a}^{2}}………\left( 1 \right)\]
According the question circle (1) passes through (0, 0) and (h, k)
\[{{\left( 0-\alpha \right)}^{2}}+{{\left( 0-a \right)}^{2}}={{a}^{2}}\]
\[\Rightarrow {{\alpha }^{2}}+{{a}^{2}}={{a}^{2}}\Rightarrow \alpha =0\]
\[{{\left( h-\alpha \right)}^{2}}+{{\left( k-a \right)}^{2}}={{a}^{2}}\]
\[\Rightarrow {{h}^{2}}-2\alpha h+{{\alpha }^{2}}+{{k}^{2}}-2ak+{{a}^{2}}={{a}^{2}}\]
\[\Rightarrow {{h}^{2}}+{{k}^{2}}-2ak+{{a}^{2}}={{a}^{2}}\,\,\left[ \because \,a=0 \right]\]
\[\therefore \,\,2a=\frac{{{h}^{2}}+{{k}^{2}}}{k}\]
Therefore, equation of the circle is
\[{{x}^{2}}+{{y}^{2}}-2ay=0\,\,\left[ Putting\,\alpha =0\,\,in\,\left( 1 \right) \right]\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}-\frac{{{h}^{2}}+{{k}^{2}}}{k}\times y=0\,\left[ \because \,\,2a=\frac{{{h}^{2}}+{{k}^{2}}}{k} \right]\]
\[\therefore k\left( {{x}^{2}}+{{y}^{2}} \right)=\left( {{h}^{2}}+{{k}^{2}} \right)y\]
| Example 07 |
Find the equation of the circle passing through the point of intersection of the circle {{x}^{2}}+{{y}^{2}}+4\left( x+y \right)+4=0 and the straight linex+y+2=0, also the center at the origin.
Solution:
\[{{x}^{2}}+{{y}^{2}}+4\left( x+y \right)+4=0………\left( 1 \right)\]
\[x+y+2=0………\left( 2 \right)\]
Equation of the circle passing through the point of intersection of (1) and (2) is
\[{{x}^{2}}+{{y}^{2}}+4\left( x+y \right)+4+k\left( x+y+2 \right)=0\]
\[\Rightarrow {{x}^{2}}+{{y}^{2}}+\left( 4+k \right)x+\left( 4+k \right)y+4+2k=0……….\left( 3 \right)\]
Now, the coordinate of the circle (3) is \left( -\frac{4+k}{2},-\frac{4+k}{2} \right)
According to the question
\[-\frac{4+k}{2}=0\]
\[\Rightarrow 4+k=0\Rightarrow k=-4\]
Therefore, equation of the required circle is
\[{{x}^{2}}+{{y}^{2}}-4=0\]
| Example 08 |
Show that the circles {{x}^{2}}+{{y}^{2}}+6x+14y+9=0 and {{x}^{2}}+{{y}^{2}}-4x-10y-7=0 touches each other externally. Find the common tangent of both the circles.
Solution:
\[{{x}^{2}}+{{y}^{2}}+6x+14y+9=0………\left( 1 \right)\]
\[{{x}^{2}}+{{y}^{2}}-4x-10y-7=0………\left( 2 \right)\]
Comparing circle (1) with the general form of the circle {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0, we have the center of the circle (1) \left( -g,-f \right)=A\left( -3,-7 \right) and radius = {{r}_{1}}=\sqrt{{{g}^{2}}+{{f}^{2}}-c}=\sqrt{9+49-9}=7
Similarly, comparing circle (2) with the general form of the circle {{x}^{2}}+{{y}^{2}}+2gx+2fy+c=0, we have the center of the circle (2) \left( -g,-f \right)=B\left( 2,5 \right) and {{r}_{1}}=\sqrt{{{g}^{2}}+{{f}^{2}}-c}=\sqrt{4+25-\left( -7 \right)}=6.
Now, the distance between the centers of both the circles
\[\overline{AB}=\sqrt{{{\left( -3-2 \right)}^{2}}+{{\left( -7-5 \right)}^{2}}}=\sqrt{25+144}=\sqrt{169}=13\]
∴ \overline{AB}=7+6={{r}_{1}}+{{r}_{2}}= Sum of the radius of the circles.
Therefore, the circles touch each other externally.
Now the equation of any curve passing through point of contact is
\[{{x}^{2}}+{{y}^{2}}+6x+14y+9+k\left( {{x}^{2}}+{{y}^{2}}-4x-10y-7 \right)=0\]
\[\Rightarrow \left( 1+k \right)\left( {{x}^{2}}+{{y}^{2}} \right)+\left( 6-4k \right)x+\left( 14-10k \right)y+9-7k=0………\left( 3 \right)\]
Equation (3) will represent a straight line if 1+k=0\Rightarrow k=-1
Putting k=-1 in (3) we have
\[10x+24y+16=0\]
\[\Rightarrow 5x+12y+8=0\]
Hence the equation of the common tangent of both the circles.
Pair of Straight Lines |
Parabola |


