কষে দেখি – 5.1
1. দুটি ঘনক তৈরি করি যার একটি বাহুর দৈর্ঘ্য যথাক্রমে 5 সেমি. ও 1 সেমি.।
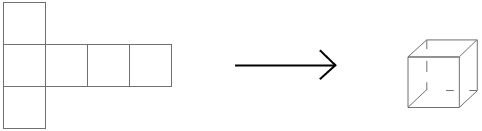
কতগুলি 1 সেমি. দৈর্ঘ্যের বাহুবিশিষ্ট ঘনক জুড়ে এই বড়ো ঘনক পাব হিসাব করে লিখি।
উত্তরঃ-
বড়ো ঘনকটির প্রতিটি বাহুর দৈর্ঘ্য 5 সেমি।
ঘনকটির আয়তন = 53 ঘন সেমি = 125 ঘন সেমি ।
ছোট ঘনকটির প্রতিটি বাহুর দৈর্ঘ্য 1 সেমি।
ঘনকটির আয়তন = 13 ঘন সেমি = 1 ঘন সেমি ।
∴ 1 সেমি দৈর্ঘ্যের বাহুর ঘনক জুড়ে এই বড়ো ঘনক তৈরি করতে 125 টি ছোট ঘনক লাগবে।
2. সুমন্ত অনেকগুলি 1 সেমি. দৈর্ঘ্যের বাহুবিশিষ্ট ঘনক তৈরি করেছে। মনামী সেই ঘনকগুলি জোড়া লাগিয়ে বড়ো ঘনক তৈরির চেষ্টা করছে। হিসাব করে দেখি নীচের কোন সংখ্যক ঘনকের ক্ষেত্রে মনামী বড়ো ঘনক তৈরি করতে পারবে।
(i) 100 (ii) 1000 (iii) 1331 (iv) 1210 (v) 3375 (vi) 2700
উত্তরঃ-
(i) 100 = 10 × 10 = 102
(ii) 1000 = 10 × 10 × 10 = 103
(iii) 1331 = 11 × 11 × 11 = 113
(iv) 324 = 18 × 18 = 182
(v) 3375 = 15 × 15 × 15 = 153
(vi) 2700 = 3 × 3 × 3 × 10 × 10 = 33 × 102
∴ মনামী সবচেয়ে বড়ো ঘনক পারবে 153 = 3375
3. নীচের সংখ্যাগুলির মধ্যে কোনটি পূর্ণঘন সংখ্যা নয় লিখি।
(i) 216 (ii) 343 (iii) 1024 (iv) 324 (v) 1744 (vi) 1372
উত্তরঃ-
(i) 216 = 2 × 2 × 2 × 3 × 3 × 3 = 23 × 33 = 63
(ii) 343 = 7 × 7 × 7 = 73
(iii) 1024 = 8 × 8 × 8 × 2 = 83 × 2
(iv) 324 = 3 × 3 × 3 × 3 × 2 × 2 = 33 × 3 × 22
(v) 1744 = 2 × 2 × 2 × 2 × 109 = 23 × 2 × 109
(vi) 1372= 7 × 7 × 7× 2 × 2 = 73 × 22
এখানে পূর্ণঘনসংখ্যা নয় – (iii) 1024, (iv) 324, (v) 1744 ও (vi) 1372
4. দেবনাথ একটি আয়তঘন তৈরি করেছে যার দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 4 সেমি., 3 সেমি., ও 3 সেমি.। হিসাব করে দেখি এইরকম কতগুলি আয়তঘন জুড়ে দেবনাথ ঘনক তৈরি করতে পারবে।
উত্তরঃ-
আয়তঘনটির দৈর্ঘ্য = 4 সেমি, প্রস্থ = 3 সেমি ও উচ্চতা = 3 সেমি
∴ আয়তঘনটির ঘনফল = 4 × 3 × 3 ঘন সেমি
আয়তঘনটিকে ঘনক হতে হলে প্রয়োজন 4 × 3 × 3 × 4 × 4 × 3 ঘন সেমি
অতিরিক্ত আয়তঘনকের প্রয়োজন = 4 × 4 × 3 টি = 48 টি।
5. নীচের সংখ্যাগুলিকে ক্ষুদ্রতম কোন ধনাত্মক সংখ্যা দিয়ে গুণ করলে গুণফল পূর্ণঘন সংখ্যা হবে হিসাব করে লিখি।
(i) 675 (ii) 200 (iii) 108 (iv) 121 (v) 1225
উত্তরঃ-
(i) 675 = 3 × 3 × 3 × 5 × 5 = 33 × 52
অর্থাৎ, 675 পূর্ণঘনসংখ্যা নয়।
কিন্তু, 33 × 52 × 5 = 33 × 53 = 3375 = 153
∴ 675 কে ক্ষুদ্রতম ধনাত্মক সংখ্যা 5 দিয়ে গুন করলে গুণফল 3375 পূর্ণঘনসংখ্যা হবে।
(ii) 200 = 2 × 2 × 2 × 5 × 5 = 23 × 52
অর্থাৎ, 200 পূর্ণঘনসংখ্যা নয়।
কিন্তু, 23 × 52 × 5 = 23 × 53 = 1000 = 103
∴ 200 কে ক্ষুদ্রতম ধনাত্মক সংখ্যা 5 দিয়ে গুন করলে গুণফল 1000 পূর্ণঘনসংখ্যা হবে।
(iii) 108 = 3 × 3 × 3 × 2 × 2 = 33 × 22
অর্থাৎ, 108 পূর্ণঘনসংখ্যা নয়।
কিন্তু, 33 × 22 × 3 = 33 × 23 = 216 = 63
∴ 108 কে ক্ষুদ্রতম ধনাত্মক সংখ্যা 2 দিয়ে গুন করলে গুণফল 216 পূর্ণঘনসংখ্যা হবে।
(iv) 121 = 11 × 11 = 112
অর্থাৎ, 121 পূর্ণঘনসংখ্যা নয়।
কিন্তু, 112 × 11 = 113 = 1331 = 113
∴ 121 কে ক্ষুদ্রতম ধনাত্মক সংখ্যা 11 দিয়ে গুন করলে গুণফল 1331 পূর্ণঘনসংখ্যা হবে।
(v) 1225 = 7 × 7 × 5 × 5 = 72 × 52
অর্থাৎ, 1225 পূর্ণঘনসংখ্যা নয়।
কিন্তু, 72 × 52 × 7 × 5 = 73 × 53 = 42875 = 353
∴ 1225 কে ক্ষুদ্রতম ধনাত্মক সংখ্যা 7 × 5 = 35 দিয়ে গুন করলে গুণফল 42875 পূর্ণঘনসংখ্যা হবে।
6. নীচের সংখ্যাগুলিকে ক্ষুদ্রতম কোন ধনাত্মক সংখ্যা দিয়ে ভাগ করলে ভাগফল পূর্ণঘন সংখ্যা হবে হিসাব করে লিখি।
(i) 7000 (ii) 2662 (iii) 4394 (iv) 6750 (v) 675
উত্তরঃ-
(i) 7000 = 10 × 10 × 10 × 7 = 103 × 7
∴ 7000 কে ক্ষুদ্রতম ধনাত্মক সংখ্যা 7 দিয়ে ভাগ করলে ভাগফলটি পূর্ণঘনসংখ্যা হবে।
(ii) 2662 = 2 × 11 × 11 × 11 = 2 × 113
∴ 2662 কে ক্ষুদ্রতম ধনাত্মক সংখ্যা 2 দিয়ে ভাগ করলে ভাগফলটি পূর্ণঘনসংখ্যা হবে।
(iii) 4394 = 13 × 13 × 13 × 2 = 133 × 2
∴ 4394 কে ক্ষুদ্রতম ধনাত্মক সংখ্যা 2 দিয়ে ভাগ করলে ভাগফলটি পূর্ণঘনসংখ্যা হবে।
(iv) 6750 = 5 × 5 × 5 × 3 × 3 × 3 × 2 = 53 × 33 × 2
∴ 6750 কে ক্ষুদ্রতম ধনাত্মক সংখ্যা 2 দিয়ে ভাগ করলে ভাগফলটি পূর্ণঘনসংখ্যা হবে।
(v) 675 = 5 × 5 × 3 × 3 × 3 = 52 × 33
∴ 675 কে ক্ষুদ্রতম ধনাত্মক সংখ্যা 5 × 5 = 25 দিয়ে ভাগ করলে ভাগফলটি পূর্ণঘনসংখ্যা হবে।
7. নীচের পূর্ণঘনসংখ্যাগুলি মৌলিক উৎপাদকে বিশ্লেষণ করি ও ঘনমূল লিখি।
(i) 512 (ii) 1728 (iii) 5832 (iv) 15625 (v) 10648
উত্তরঃ-
(i) 512 = 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 × 2 = 23 × 23 × 23 = 83
∴ ∛512 = 8
(ii) 1721 = 2 × 2 × 2 × 2 × 2 × 2 × 3 × 3 × 3 = 23 × 23 × 33 = 123
∴ ∛1721 = 12
(iii) 5832 = 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3 = 23 × 33 × 33 = 183
∴ ∛5832 = 18
(iv) 15625 = 5 × 5 × 5 × 5 × 5 × 5 = 53 × 53 = 253
∴ ∛15625 = 25
(v) 10648 = 2 × 2 × 2 × 11 × 11 × 11 = 23 × 113 = 223
∴ ∛10648 = 22
কষে দেখি – 5.2
1.
| ঘনকের বাহুর দৈর্ঘ্য (একক) | ঘনকের আয়তন (ঘন একক) | |
| (i) | \[{{p}^{2}}+{{q}^{2}}\] | |
| (ii) | \[\frac{x}{3}+\frac{4}{y}\] | |
| (iii) | \[{{x}^{2}}y-{{z}^{2}}\] | |
| (iv) | \[l+b-2c\] | |
| (v) | \[{{\left( 2.89 \right)}^{3}}+{{\left( 2.11 \right)}^{3}}+15\times 2.89\times 2.11\] | |
| (vi) | \[{{\left( 2m+3n \right)}^{3}}+{{\left( 2m-3n \right)}^{3}}+15\left( 4{{m}^{2}}-9{{n}^{2}} \right)\] | |
| (vii) | \[{{\left( a+b \right)}^{3}}-{{\left( a-b \right)}^{3}}-6b\left( {{a}^{2}}-{{b}^{2}} \right)\] | |
| (viii) | \[2x-3y-4z\] | |
| (ix) | \[{{x}^{6}}-15{{x}^{4}}+75{{x}^{2}}-125\] | |
| (x) | \[1000+30x\left( 10+x \right)+{{x}^{3}}\] |
উত্তরঃ-
| ঘনকের বাহুর দৈর্ঘ্য (একক) | ঘনকের আয়তন (ঘন একক) | |
| (i) | \[{{p}^{2}}+{{q}^{2}}\] | \[{{\left( {{p}^{2}}+{{q}^{2}} \right)}^{3}}={{\left( {{p}^{2}} \right)}^{3}}+3.{{\left( {{p}^{2}} \right)}^{2}}.{{q}^{2}}+3.{{p}^{2}}.{{\left( {{q}^{2}} \right)}^{2}}+{{\left( {{q}^{2}} \right)}^{3}}\] \[={{p}^{6}}+3{{p}^{4}}{{q}^{2}}+3{{p}^{2}}{{q}^{4}}+{{q}^{6}}\] |
| (ii) | \[\frac{x}{3}+\frac{4}{y}\] | \[{{\left( \frac{x}{3}+\frac{4}{y} \right)}^{3}}={{\left( \frac{x}{3} \right)}^{3}}+3{{\left( \frac{x}{3} \right)}^{2}}\left( \frac{4}{y} \right)+3\left( \frac{x}{3} \right){{\left( \frac{4}{y} \right)}^{2}}+{{\left( \frac{4}{y} \right)}^{3}}\] \[=\frac{{{x}^{3}}}{27}+\frac{4{{x}^{2}}}{3y}+\frac{16x}{{{y}^{2}}}+\frac{64}{{{y}^{3}}}\] |
| (iii) | \[{{x}^{2}}y-{{z}^{2}}\] | \[{{\left( {{x}^{2}}y-{{z}^{2}} \right)}^{3}}={{\left( {{x}^{2}}y \right)}^{3}}-3{{\left( {{x}^{2}}y \right)}^{2}}\left( {{z}^{2}} \right)+3\left( {{x}^{2}}y \right){{\left( {{z}^{2}} \right)}^{2}}-{{\left( {{z}^{2}} \right)}^{3}}\] \[={{x}^{6}}{{y}^{3}}-3{{x}^{4}}{{y}^{2}}{{z}^{2}}+3{{x}^{2}}y{{z}^{4}}-{{z}^{6}}\] |
| (iv) | \[l+b-2c\] | \[{{\left( l+b-2c \right)}^{3}}\] \[={{l}^{3}}+{{b}^{3}}-8{{c}^{3}}+3{{l}^{2}}b+3l{{b}^{2}}-6c{{l}^{2}}-12lbc-6{{b}^{2}}c-12{{c}^{2}}l+12{{c}^{2}}b\] |
| (v) | \[\left( 2.89+2.11 \right)\] | \[{{\left( 2.89 \right)}^{3}}+{{\left( 2.11 \right)}^{3}}+15\times 2.89\times 2.11\] |
| (vi) | \[\left( 2m+3n \right)+\left( 2m-3n \right)\] | \[{{\left( 2m+3n \right)}^{3}}+{{\left( 2m-3n \right)}^{3}}+15\left( 4{{m}^{2}}-9{{n}^{2}} \right)\] |
| (vii) | \[\left( a+b \right)-\left( a-b \right)\] | \[{{\left( a+b \right)}^{3}}-{{\left( a-b \right)}^{3}}-6b\left( {{a}^{2}}-{{b}^{2}} \right)\] |
| (viii) | \[2x-3y-4z\] | \[{{\left( 2x-3y-4z \right)}^{3}}\] \[=8{{x}^{3}}-27{{y}^{3}}-64{{z}^{3}}-36{{x}^{2}}y+54x{{y}^{2}}-48{{x}^{2}}z+144xyz-108{{y}^{2}}z+96xy{{z}^{2}}-144y{{z}^{2}}\] |
| (ix) | \[{{x}^{2}}-5\] | \[{{x}^{6}}-15{{x}^{4}}+75{{x}^{2}}-125\] |
| (x) | \[10+x\] | \[1000+30x\left( 10+x \right)+{{x}^{3}}\] |
2. I থেকে IV নং অভেদের সাহায্যে নিচের প্রশ্নগুলি সমাধান করি।
a) x-y=2 হলে x^3-y^3-6xy-এর মান হিসাব করে লিখি।
b) a+b=-\frac13 হলে প্রমাণ করার চেষ্টা করি a^3+b^3-ab\; =-\frac1{27}
c) x+y=2 এবং \frac1x+\frac1y=2 হলে x^3+y^3-এর মান হিসাব করে লিখি।
d) \frac{x^2-1}x=2 হলে \frac{x^6-1}{x^3}-এর মান হিসাব করে লেখার চেষ্টা করি।
e) x+\frac1x=5 হলে x^3+\frac1{x^3}-এর মান হিসাব করে লিখি।
f) x=y+z হলে x^3-y^3-z^3-3xyz-এর মান হিসাব করে লিখি।
g) xy\left(x+y\right)=m হলে x^3+y^3+3m=\frac{m^3}{x^3y^3} প্রমান করার চেষ্টা করি।
h) 2x+\frac1{3x}=4 হলে প্রমান করার চেষ্টা করি 27x^3+\frac1{8x^3}=189
i) 2a-\frac2a+1=0 হলে, a^3-\frac1{a^3}+2-এর মান হিসাব করে লিখি।
j) a^3+b^3+c^3=3abc হলে (a+b+c) –এর মান হিসাব করে লিখি \left(a\neq b\neq c\right) ।
k) যদি m+n=5 এবং mn=6 হয় তবে \left(m^2+n^2\right)\left(m^3+n^3\right)-এর মান হিসাব করে লিখি।
উত্তরঃ-
(a) দেওয়া আছে, x-y=2
\[{{x}^{3}}-{{y}^{3}}-6xy\]
\[={{x}^{3}}-{{y}^{3}}-3xy\left( 2 \right)\]
\[={{x}^{3}}-{{y}^{3}}-3xy\left( x-y \right)\]
\[={{\left( x-y \right)}^{3}}\]
\[={{\left( 2 \right)}^{3}}\]
\[=8\]
(b) দেওয়া আছে, a+b=-\frac{1}{3}
বামপক্ষ,
\[{{a}^{3}}+{{b}^{3}}-ab\]
\[={{a}^{3}}+{{b}^{3}}+3ab\left( -\frac{1}{3} \right)\]
\[={{a}^{3}}+{{b}^{3}}+3ab\left( a+b \right)\]
\[={{\left( a+b \right)}^{3}}\]
\[={{\left( -\frac{1}{3} \right)}^{3}}\]
\[=-\frac{1}{27}\]
= ডানপক্ষ (প্রমানিত)।
(c) দেওয়া আছে, x+y=2 এবং \frac{1}{x}+\frac{1}{y}=2
\[\Rightarrow \frac{y+x}{xy}=2\]
\[\Rightarrow x+y=2xy\]
\[\Rightarrow 2=2xy\]
\[\Rightarrow xy=1\]
এবার,
\[{{x}^{3}}+{{y}^{3}}\]
\[={{\left( x+y \right)}^{3}}-3xy\left( x+y \right)\]
\[={{\left( 2 \right)}^{3}}-3\left( 1 \right)\left( 2 \right)\]
\[=8-6\]
\[=2\]
(d) দেওয়া আছে, \frac{{{x}^{2}}-1}{x}=2
\[\Rightarrow x-\frac{1}{x}=2\]
এবার,
\[\frac{{{x}^{6}}-1}{{{x}^{3}}}\]
\[=\frac{{{x}^{6}}}{{{x}^{3}}}-\frac{1}{{{x}^{3}}}\]
\[={{x}^{3}}-\frac{1}{{{x}^{3}}}\]
\[={{\left( x-\frac{1}{x} \right)}^{3}}+3.x.\frac{1}{x}\left( x-\frac{1}{x} \right)\]
\[={{\left( 2 \right)}^{3}}+3\left( 2 \right)\]
\[=8+6=14\]
(e) দেওয়া আছে, x+\frac{1}{x}=5
এবার,
\[{{x}^{3}}+\frac{1}{{{x}^{3}}}\]
\[={{\left( x+\frac{1}{x} \right)}^{3}}-3.x.\frac{1}{x}\left( x+\frac{1}{x} \right)\]
\[={{\left( 5 \right)}^{3}}-3\left( 5 \right)\]
\[=125-15\]
\[=110\]
(f) দেওয়া আছে, x=y+z
এবার,
\[{{x}^{3}}-{{y}^{3}}-{{z}^{3}}-3xyz\]
\[={{\left( y+z \right)}^{3}}-{{y}^{3}}-{{z}^{3}}-3\left( y+z \right)yz\]
\[={{y}^{3}}+{{z}^{3}}+3yz\left( y+z \right)-{{y}^{3}}-{{z}^{3}}-3yz\left( y+z \right)\]
\[=0\]
(g) দেওয়া আছে, xy\left( x+y \right)=m
\[\Rightarrow \left( x+y \right)=\frac{m}{xy}\]
বামপক্ষ,
\[{{x}^{3}}+{{y}^{3}}+3m\]
\[={{\left( x+y \right)}^{3}}-3xy\left( x+y \right)+3m\]
\[={{\left( \frac{m}{xy} \right)}^{3}}-3m+3m\]
\[=\frac{{{m}^{3}}}{{{x}^{3}}{{y}^{3}}}\]
= ডানপক্ষ (প্রমানিত)।
(h) দেওয়া আছে, 2x+\frac{1}{3x}=4
\[\Rightarrow 6{{x}^{2}}+1=12x\]
\[\Rightarrow 2x\left( 3x+\frac{1}{2x} \right)=12x\]
\[\Rightarrow 3x+\frac{1}{2x}=6\]
বামপক্ষ,
\[27{{x}^{3}}+\frac{1}{8{{x}^{3}}}\]
\[={{\left( 3x \right)}^{3}}+{{\left( \frac{1}{2x} \right)}^{3}}\]
\[={{\left( 3x+\frac{1}{2x} \right)}^{3}}-3.3x.\frac{1}{2x}\left( 3x+\frac{1}{2x} \right)\]
\[={{\left( 6 \right)}^{3}}-\frac{9}{2}\left( 6 \right)\]
\[=216-27\]
\[=189\]
= ডানপক্ষ (প্রমানিত)।
(i) দেওয়া আছে, 2a-\frac{2}{a}+1=0
\[\Rightarrow 2a-\frac{2}{a}=-1\]
\[\Rightarrow 2\left( a-\frac{1}{a} \right)=-1\]
\[\Rightarrow a-\frac{1}{a}=-\frac{1}{2}\]
এবার,
\[{{a}^{3}}-\frac{1}{{{a}^{3}}}+2\]
\[=\left\{ {{\left( a-\frac{1}{a} \right)}^{3}}+3.a.\frac{1}{a}\left( a-\frac{1}{a} \right) \right\}+2\]
\[=\left\{ {{\left( -\frac{1}{2} \right)}^{3}}+3\left( -\frac{1}{2} \right) \right\}+2\]
\[=-\frac{1}{8}-\frac{3}{2}+2\]
\[=\frac{-1-12+16}{8}\]
\[=\frac{3}{8}\]
(j) দেওয়া আছে, {{a}^{3}}+{{b}^{3}}+{{c}^{3}}=3abc
\[\Rightarrow {{a}^{3}}+{{b}^{3}}+{{c}^{3}}-3abc=0\]
\[\Rightarrow \left( a+b+c \right)\left( {{a}^{2}}+{{b}^{2}}+{{c}^{2}}-ab-bc-ca \right)=0\]
হয়, a+b+c=0 নতুবা, {{a}^{2}}+{{b}^{2}}+{{c}^{2}}-ab-bc-ca=0
\[\therefore a+b+c=0\]
(k) দেওয়া আছে, m+n=5,mn=6
এবার,
\[\left( {{m}^{2}}+{{n}^{2}} \right)\left( {{m}^{3}}+{{n}^{3}} \right)\]
\[=\left\{ {{\left( m+n \right)}^{2}}-2mn \right\}\left\{ {{\left( m+n \right)}^{3}}-3mn\left( m+n \right) \right\}\]
\[=\left\{ {{\left( 5 \right)}^{2}}-2\left( 6 \right) \right\}\left\{ {{\left( 5 \right)}^{3}}-3\left( 6 \right)\left( 5 \right) \right\}\]
\[=\left\{ 25-12 \right\}\left\{ 125-90 \right\}\]
\[=13\times 35\]
\[=455\]
কষে দেখি – 5.3
1. ফাঁকা ঘরে বুঝে লিখিঃ
| প্রথম বীজগানিতিক সংখ্যামালা | দ্বিতীয় বীজগানিতিক সংখ্যামালা | \[{{a}^{3}}+{{b}^{3}}=\left[ {} \right]\times \left[ {} \right]\] \[{{a}^{3}}-{{b}^{3}}=\left[ {} \right]\times \left[ {} \right]\] অভেদের সাহায্যে প্রথম ও দ্বিতীয়ের গুণফল |
| \[(i)x+9\] | \[{{x}^{2}}-9x+81\] | |
| \[(ii)2a-1\] | \[=8{{a}^{3}}-1\] \[={{\left( 2a \right)}^{3}}-{{\left( 1 \right)}^{3}}\] \[\left( 2a-1 \right)\left\{ {{\left( 2a \right)}^{2}}+2a\times 1+{{\left( 1 \right)}^{2}} \right\}\] \[\left( 2a-1 \right)\left( 4{{a}^{2}}+2a+1 \right)\] | |
| \[(iii)3-5c\] | \[27-125{{c}^{3}}\] | |
| \[(iv)\left( a+b+c \right)\] | \[{{\left( a+b \right)}^{2}}-\left( a+b \right)c+{{c}^{2}}\] | |
| \[(v)3x\] | \[{{\left( 2x+1 \right)}^{2}}-\left( 2x+1 \right)\left( x+1 \right)+{{\left( x+1 \right)}^{2}}\] | |
| \[\left( vi \right)\frac{x}{y}+1\] | \[\frac{{{x}^{2}}}{{{y}^{2}}}-\frac{x}{y}+1\] | |
| \[\left( vii \right)4a-5b\] | \[16{{a}^{2}}+20ab+25{{b}^{2}}\] | |
| \[\left( viii \right)\] | \[{{a}^{2}}{{b}^{2}}+abcd+{{c}^{2}}{{d}^{2}}\] | \[{{a}^{3}}{{b}^{3}}-{{c}^{3}}{{d}^{3}}\] |
| \[\left( ix \right)1-4y\] | \[1-64{{y}^{3}}\] | |
| \[\left( x \right)\left( 2p+1 \right)\] | \[8{{\left( p-3 \right)}^{3}}+343\] | |
| \[\left( xi \right)\left( m-p \right)\] | \[{{\left( m+n \right)}^{2}}+\left( m+n \right)\left( n+p \right)+{{\left( n+p \right)}^{2}}\] | |
| \[\left( xii \right)\left( a+b \right)\] | \[{{\left( 3a-2b \right)}^{2}}+\left( 3a-2b \right)\left( 2a-3b \right)+{{\left( 2a-3b \right)}^{2}}\] |
উত্তরঃ-
| প্রথম বীজগানিতিক সংখ্যামালা | দ্বিতীয় বীজগানিতিক সংখ্যামালা | \[{{a}^{3}}+{{b}^{3}}=\left( a+b \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right)\] \[{{a}^{3}}-{{b}^{3}}=\left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right)\] অভেদের সাহায্যে প্রথম ও দ্বিতীয়ের গুণফল |
| \[(i)x+9\] | \[{{x}^{2}}-9x+81\] | \[{{x}^{3}}+729\] |
| \[(ii)2a-1\] | \[4{{a}^{2}}+2a+1\] | \[\left( 2a-1 \right)\left\{ {{\left( 2a \right)}^{2}}+2a\times 1+{{\left( 1 \right)}^{2}} \right\}\] \[={{\left( 2a \right)}^{3}}-{{\left( 1 \right)}^{3}}\] \[=8{{a}^{3}}-1\] |
| \[(iii)3-5c\] | \[9+15c+25{{c}^{2}}\] | \[27-125{{c}^{3}}\] |
| \[(iv)\left( a+b+c \right)\] | \[{{\left( a+b \right)}^{2}}-\left( a+b \right)c+{{c}^{2}}\] | \[{{\left( a+b \right)}^{3}}+{{c}^{3}}\] |
| \[(v)3x\] | \[{{\left( 2x+1 \right)}^{2}}-\left( 2x+1 \right)\left( x+1 \right)+{{\left( x+1 \right)}^{2}}\] | \[27{{x}^{3}}\] |
| \[\left( vi \right)\frac{x}{y}+1\] | \[\frac{{{x}^{2}}}{{{y}^{2}}}-\frac{x}{y}+1\] | \[\frac{{{x}^{3}}}{{{y}^{3}}}+1\] |
| \[\left( vii \right)4a-5b\] | \[16{{a}^{2}}+20ab+25{{b}^{2}}\] | \[64{{a}^{3}}-125{{b}^{3}}\] |
| \[\left( viii \right)ab-cd\] | \[{{a}^{2}}{{b}^{2}}+abcd+{{c}^{2}}{{d}^{2}}\] | \[{{a}^{3}}{{b}^{3}}-{{c}^{3}}{{d}^{3}}\] |
| \[\left( ix \right)1-4y\] | \[1+4y+16{{y}^{2}}\] | \[1-64{{y}^{3}}\] |
| \[\left( x \right)\left( 2p+1 \right)\] | \[{{\left( 2p-6 \right)}^{2}}-14\left( p-3 \right)+49\] | \[8{{\left( p-3 \right)}^{3}}+343\] |
| \[\left( xi \right)\left( m-p \right)\] | \[{{\left( m+n \right)}^{2}}+\left( m+n \right)\left( n+p \right)+{{\left( n+p \right)}^{2}}\] | \[{{\left( m+n \right)}^{3}}-{{\left( n+p \right)}^{3}}\] |
| \[\left( xii \right)\left( a+b \right)\] | \[{{\left( 3a-2b \right)}^{2}}+\left( 3a-2b \right)\left( 2a-3b \right)+{{\left( 2a-3b \right)}^{2}}\] | \[{{\left( 3a-2b \right)}^{3}}-{{\left( 2a-3b \right)}^{3}}\] |
2. সরল করি [ সূত্রের সাহায্যে ]
\[\left( i \right)\left( a+b \right)\left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right)\]
\[\left( ii \right)\left( a-2b \right)\left( {{a}^{2}}+2ab+4{{b}^{2}} \right)\left( {{a}^{3}}+8{{b}^{3}} \right)\]
\[\left( iii \right)\left( 4{{a}^{2}}-9 \right)\left( 4{{a}^{2}}-6a+9 \right)\left( 4{{a}^{2}}+6a+9 \right)\]
\[\left( iv \right)\left( x-y \right)\left( {{x}^{2}}+xy+{{y}^{2}} \right)+\left( y-z \right)\left( {{y}^{2}}+yz+{{z}^{2}} \right)+\left( z-x \right)\left( {{z}^{2}}+zx+{{x}^{2}} \right)\]
\[\left( v \right)\left( x+1 \right)\left( {{x}^{2}}-x+1 \right)+\left( 2x-1 \right)\left( 4{{x}^{2}}+2x+1 \right)-\left( x-1 \right)\left( {{x}^{2}}+x+1 \right)\]
উত্তরঃ-
\[\left( i \right)\left( a+b \right)\left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right)\]
\[=\left\{ \left( a+b \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right) \right\}\left\{ \left( a-b \right)\left( {{a}^{2}}+ab+{{b}^{2}} \right) \right\}\]
\[=\left( {{a}^{3}}+{{b}^{3}} \right)\left( {{a}^{3}}-{{b}^{3}} \right)\]
\[={{\left( {{a}^{3}} \right)}^{2}}-{{\left( {{b}^{3}} \right)}^{2}}\]
\[={{a}^{6}}-{{b}^{6}}\]
\[\left( ii \right)\left( a-2b \right)\left( {{a}^{2}}+2ab+4{{b}^{2}} \right)\left( {{a}^{3}}+8{{b}^{3}} \right)\]
\[=\left\{ \left( a-2b \right)\left( {{a}^{2}}+a\left( 2b \right)+{{\left( 2b \right)}^{2}} \right) \right\}\left( {{a}^{3}}+8{{b}^{3}} \right)\]
\[=\left\{ {{a}^{3}}-{{\left( 2b \right)}^{3}} \right\}\left( {{a}^{3}}+8{{b}^{3}} \right)\]
\[=\left( {{a}^{3}}-8{{b}^{3}} \right)\left( {{a}^{3}}+8{{b}^{3}} \right)\]
\[={{\left( {{a}^{3}} \right)}^{2}}-{{\left( 8{{b}^{3}} \right)}^{2}}\]
\[={{a}^{6}}-64{{b}^{6}}\]
\[\left( iii \right)\left( 4{{a}^{2}}-9 \right)\left( 4{{a}^{2}}-6a+9 \right)\left( 4{{a}^{2}}+6a+9 \right)\]
\[=\left\{ {{\left( 2a \right)}^{2}}-{{\left( 3 \right)}^{2}} \right\}\left( 4{{a}^{2}}-6a+9 \right)\left( 4{{a}^{2}}+6a+9 \right)\]
\[=\left( 2a+3 \right)\left( 2a-3 \right)\left( 4{{a}^{2}}-6a+9 \right)\left( 4{{a}^{2}}+6a+9 \right)\]
\[=\left\{ \left( 2a+3 \right)\left( 4{{a}^{2}}-6a+9 \right) \right\}\left\{ \left( 2a-3 \right)\left( 4{{a}^{2}}+6a+9 \right) \right\}\]
\[=\left[ \left( 2a+3 \right)\left\{ {{\left( 2a \right)}^{2}}-2a\times 3+{{\left( 3 \right)}^{2}} \right\} \right]\left[ \left( 2a-3 \right)\left\{ {{\left( 2a \right)}^{2}}+2a\times 3+{{\left( 3 \right)}^{2}} \right\} \right]\]
\[=\left\{ {{\left( 2a \right)}^{3}}+{{\left( 3 \right)}^{3}} \right\}\left\{ {{\left( 2a \right)}^{3}}-{{\left( 3 \right)}^{3}} \right\}\]
\[=\left( 8{{a}^{3}}+27 \right)\left( 8{{a}^{3}}-27 \right)\]
\[={{\left( 8{{a}^{3}} \right)}^{2}}-{{\left( 27 \right)}^{2}}\]
\[=64{{a}^{6}}-729\]
\[\left( iv \right)\left( x-y \right)\left( {{x}^{2}}+xy+{{y}^{2}} \right)+\left( y-z \right)\left( {{y}^{2}}+yz+{{z}^{2}} \right)+\left( z-x \right)\left( {{z}^{2}}+zx+{{x}^{2}} \right)\]
\[={{x}^{3}}-{{y}^{3}}+{{y}^{3}}-{{z}^{3}}+{{z}^{3}}-{{x}^{3}}\]
\[=0\]
\[\left( v \right)\left( x+1 \right)\left( {{x}^{2}}-x+1 \right)+\left( 2x-1 \right)\left( 4{{x}^{2}}+2x+1 \right)-\left( x-1 \right)\left( {{x}^{2}}+x+1 \right)\]
\[={{x}^{3}}+1+8{{x}^{3}}-1-{{x}^{3}}+1\]
\[=8{{x}^{3}}+1\]
3. x+\frac1x=-1 হলে x^3-1 এর মান কি হবে হিসাব করে লিখি।
উত্তরঃ-
দেওয়া আছে, x+\frac{1}{x}=-1
\[\Rightarrow \frac{{{x}^{2}}+1}{x}=-1\]
\[\Rightarrow {{x}^{2}}+1=-x\]
\[\Rightarrow {{x}^{2}}+x+1=0\]
এবার,
\[{{x}^{3}}-1\]
\[=\left( x-1 \right)\left( {{x}^{2}}+x+1 \right)\]
\[=\left( x-1 \right)\left( 0 \right)\]
\[=0\]
4. a+\frac9a=3 হলে a^3+27 এর মান কি হবে হিসাব করে লিখি।
উত্তরঃ-
দেওয়া আছে, a+\frac{9}{a}=3
\[\Rightarrow \frac{{{a}^{2}}+9}{a}=3\]
\[\Rightarrow {{a}^{2}}+9=3a\]
\[\Rightarrow {{a}^{2}}-3a+9=0\]
এবার,
\[{{a}^{3}}+27\]
\[={{\left( a \right)}^{3}}+{{\left( 3 \right)}^{3}}\]
\[=\left( a+3 \right)\left( {{a}^{2}}-3a+9 \right)\]
\[=\left( a+3 \right)\left( 0 \right)\]
\[=0\]
5. \frac ab+\frac ba=1হলে a^3+b^3এর মান কি হবে হিসাব করে লিখি।
উত্তরঃ-
দেওয়া আছে, \frac{a}{b}+\frac{b}{a}=1
\[\Rightarrow \frac{{{a}^{2}}+{{b}^{2}}}{ab}=1\]
\[\Rightarrow {{a}^{2}}+{{b}^{2}}=ab\]
\[\Rightarrow {{a}^{2}}-ab+{{b}^{2}}=0\]
এবার,
\[{{a}^{3}}+{{b}^{3}}\]
\[=\left( a+b \right)\left( {{a}^{2}}-ab+{{b}^{2}} \right)\]
\[=\left( a+b \right)\left( 0 \right)\]
\[=0\]
6. নিচের বীজগাণিতিক সঙ্খামালাগুলিকে উৎপাদকে বিশ্লেষণ করি।
\[\left( i \right)1000{{a}^{3}}+27{{b}^{6}}\]
\[\left( ii \right)1-216{{z}^{3}}\]
\[\left( iii \right){{m}^{4}}-m\]
\[\left( iv \right)192{{a}^{3}}+3\]
\[\left( v \right)16{{a}^{4}}{{x}^{3}}+54a{{y}^{3}}\]
\[\left( vi \right)729{{a}^{3}}{{b}^{3}}{{c}^{3}}-125\]
\[\left( vii \right)\frac{27}{{{a}^{3}}}-\frac{1}{27{{b}^{3}}}\]
\[\left( viii \right)\frac{{{x}^{3}}}{64}-\frac{64}{{{x}^{3}}}\]
\[\left( ix \right){{x}^{3}}+3{{x}^{2}}y+3x{{y}^{2}}+2{{y}^{3}}\]
\[\left( x \right)1+9x+27{{x}^{2}}+28{{x}^{3}}\]
\[\left( xi \right){{x}^{3}}-9{{y}^{3}}-3xy\left( x-y \right)\]
\[\left( xii \right)8-{{a}^{3}}+3{{a}^{2}}b-3a{{b}^{2}}+{{b}^{3}}\]
\[\left( xiii \right){{x}^{6}}+3{{x}^{4}}{{b}^{2}}+3{{x}^{2}}{{b}^{4}}+{{b}^{6}}+{{a}^{3}}{{b}^{3}}\]
\[\left( xiv \right){{x}^{6}}+27\]
\[\left( xv \right){{x}^{6}}-{{y}^{6}}\]
\[\left( xvi \right){{x}^{12}}-{{y}^{12}}\]
\[\left( xvii \right){{m}^{3}}-{{n}^{3}}-m\left( {{m}^{2}}-{{n}^{2}} \right)+n{{\left( m-n \right)}^{2}}\]
উত্তরঃ-
\[\left( i \right)1000{{a}^{3}}+27{{b}^{6}}\]
\[={{\left( 10a \right)}^{3}}+{{\left( 3{{b}^{2}} \right)}^{3}}\]
\[=\left( 10a+3{{b}^{2}} \right)\left\{ {{\left( 10a \right)}^{2}}-10a\times 3{{b}^{2}}+\left( 3{{b}^{2}} \right) \right\}\]
\[=\left( 10a+3{{b}^{2}} \right)\left( 100{{a}^{2}}-30{{a}^{2}}+9{{b}^{4}} \right)\]
\[\left( ii \right)1-216{{z}^{3}}\]
\[={{\left( 1 \right)}^{3}}-{{\left( 6z \right)}^{3}}\]
\[=\left( 1-6z \right)\left\{ {{\left( 1 \right)}^{2}}+1\times 6z+{{\left( 6z \right)}^{2}} \right\}\]
\[=\left( 1-6z \right)\left( 1+6z+36{{z}^{2}} \right)\]
\[\left( iii \right){{m}^{4}}-m\]
\[=m\left( {{m}^{3}}-1 \right)\]
\[=m\left( m-1 \right)\left( {{m}^{2}}+m+1 \right)\]
\[\left( iv \right)192{{a}^{3}}+3\]
\[=3\left( 64{{a}^{3}}+1 \right)\]
\[=3\left\{ {{\left( 4a \right)}^{3}}+{{\left( 1 \right)}^{3}} \right\}\]
\[=3\left( 4a+1 \right)\left( 16{{a}^{2}}-4a+1 \right)\]
\[\left( v \right)16{{a}^{4}}{{x}^{3}}+54a{{y}^{3}}\]
\[=2a\left( 8{{a}^{3}}{{x}^{3}}+27{{y}^{3}} \right)\]
\[=2a\left\{ {{\left( 2ax \right)}^{3}}+{{\left( 3y \right)}^{3}} \right\}\]
\[=2a\left( 2ax+3y \right)\left\{ {{\left( 2ax \right)}^{2}}-2ax\times 3y+{{\left( 3y \right)}^{2}} \right\}\]
\[=2a\left( 2ax+3y \right)\left( 4{{a}^{2}}{{x}^{2}}-6axy+9{{y}^{2}} \right)\]
\[\left( vi \right)729{{a}^{3}}{{b}^{3}}{{c}^{3}}-125\]
\[={{\left( 9abc \right)}^{3}}-{{\left( 5 \right)}^{3}}\]
\[=\left( 9abc-5 \right)\left( 81{{a}^{2}}{{b}^{2}}{{c}^{2}}+45abc+25 \right)\]
\[\left( vii \right)\frac{27}{{{a}^{3}}}-\frac{1}{27{{b}^{3}}}\]
\[={{\left( \frac{3}{a} \right)}^{3}}-{{\left( \frac{1}{3b} \right)}^{3}}\]
\[=\left( \frac{3}{a}-\frac{1}{3b} \right)\left\{ {{\left( \frac{3}{a} \right)}^{2}}+\frac{3}{a}\times \frac{1}{3b}+{{\left( \frac{1}{3b} \right)}^{2}} \right\}\]
\[=\left( \frac{3}{a}-\frac{1}{3b} \right)\left( \frac{9}{{{a}^{3}}}+\frac{1}{ab}+\frac{1}{9{{b}^{2}}} \right)\]
\[\left( viii \right)\frac{{{x}^{3}}}{64}-\frac{64}{{{x}^{3}}}\]
\[={{\left( \frac{x}{4} \right)}^{3}}-{{\left( \frac{4}{x} \right)}^{3}}\]
\[=\left( \frac{x}{4}-\frac{4}{x} \right)\left\{ {{\left( \frac{x}{4} \right)}^{2}}+\frac{x}{4}\times \frac{4}{x}+{{\left( \frac{4}{x} \right)}^{2}} \right\}\]
\[=\left( \frac{x}{4}-\frac{4}{x} \right)\left( \frac{{{x}^{2}}}{16}+1+\frac{16}{{{x}^{2}}} \right)\]
\[=\left( \frac{x}{4}-\frac{4}{x} \right)\left\{ {{\left( \frac{x}{4} \right)}^{2}}+{{\left( \frac{4}{x} \right)}^{2}}+1 \right\}\]
\[=\left( \frac{x}{4}-\frac{4}{x} \right)\left\{ {{\left( \frac{x}{4}+\frac{4}{x} \right)}^{2}}-2\times \frac{x}{4}\times \frac{4}{x}+1 \right\}\]
\[=\left( \frac{x}{4}-\frac{4}{x} \right)\left\{ {{\left( \frac{x}{4}+\frac{4}{x} \right)}^{2}}-1 \right\}\]
\[=\left( \frac{x}{4}-\frac{4}{x} \right)\left( \frac{x}{4}+\frac{4}{x}+1 \right)\left( \frac{x}{4}-\frac{4}{x}-1 \right)\]
\[\left( ix \right){{x}^{3}}+3{{x}^{2}}y+3x{{y}^{2}}+2{{y}^{3}}\]
\[={{x}^{3}}+3{{x}^{2}}y+3x{{y}^{2}}+{{y}^{3}}+{{y}^{3}}\]
\[={{\left( x+y \right)}^{3}}+{{y}^{3}}\]
\[=\left( x+y+y \right)\left\{ {{\left( x+y \right)}^{2}}-\left( x+y \right)y+{{y}^{2}} \right\}\]
\[=\left( x+2y \right)\left( {{x}^{2}}+2xy+{{y}^{2}}-xy-{{y}^{2}}+{{y}^{2}} \right)\]
\[=\left( x+2y \right)\left( {{x}^{2}}+xy+{{y}^{2}} \right)\]
\[\left( x \right)1+9x+27{{x}^{2}}+28{{x}^{3}}\]
\[=\left( 1+9x+27{{x}^{2}}+27{{x}^{3}} \right)+{{x}^{3}}\]
\[=\left\{ {{\left( 1 \right)}^{3}}+3\times {{\left( 1 \right)}^{2}}\times 3x+3\times 1\times {{\left( 3x \right)}^{2}}+{{\left( 3x \right)}^{3}} \right\}+{{x}^{3}}\]
\[={{\left( 1+3x \right)}^{3}}+{{\left( x \right)}^{3}}\]
\[=\left( 1+3x+x \right)\left\{ {{\left( 1+3x \right)}^{2}}-\left( 1+3x \right)x+{{x}^{2}} \right\}\]
\[=\left( 1+4x \right)\left( 1+6x+9{{x}^{2}}-3x-3{{x}^{2}}+{{x}^{2}} \right)\]
\[=\left( 1+4x \right)\left( 1+3x+7{{x}^{2}} \right)\]
\[\left( xi \right){{x}^{3}}-9{{y}^{3}}-3xy\left( x-y \right)\]
\[={{x}^{3}}-9{{y}^{3}}-3{{x}^{2}}y+3x{{y}^{2}}\]
\[={{x}^{3}}-3{{x}^{2}}y+3x{{y}^{2}}-{{y}^{3}}-8{{y}^{3}}\]
\[={{\left( x-y \right)}^{3}}-{{\left( 2y \right)}^{3}}\]
\[=\left( x-y-2y \right)\left\{ {{\left( x-y \right)}^{2}}+\left( x-y \right)2y+{{\left( 2y \right)}^{2}} \right\}\]
\[=\left( x-3y \right)\left( {{x}^{2}}-2xy+{{y}^{2}}+2xy-2{{y}^{2}}+4{{y}^{2}} \right)\]
\[=\left( x-3y \right)\left( {{x}^{2}}+3{{y}^{2}} \right)\]
\[\left( xii \right)8-{{a}^{3}}+3{{a}^{2}}b-3a{{b}^{2}}+{{b}^{3}}\]
\[={{\left( 2 \right)}^{3}}-\left( {{a}^{3}}-3{{a}^{2}}b+3a{{b}^{2}}-{{b}^{3}} \right)\]
\[={{\left( 2 \right)}^{3}}-{{\left( a-b \right)}^{3}}\]
\[=\left\{ 2-\left( a-b \right) \right\}\left\{ {{\left( 2 \right)}^{2}}+2\left( a-b \right)+{{\left( a-b \right)}^{2}} \right\}\]
\[=\left( 2-a+b \right)\left( 4+2a-2b+{{a}^{2}}-2ab+{{b}^{2}} \right)\]
\[\left( xiii \right){{x}^{6}}+3{{x}^{4}}{{b}^{2}}+3{{x}^{2}}{{b}^{4}}+{{b}^{6}}+{{a}^{3}}{{b}^{3}}\]
\[={{\left( {{x}^{2}} \right)}^{3}}+3{{\left( {{x}^{2}} \right)}^{2}}{{b}^{2}}+3{{x}^{2}}{{\left( {{b}^{2}} \right)}^{2}}+{{\left( {{b}^{2}} \right)}^{3}}+{{a}^{3}}{{b}^{3}}\]
\[={{\left( {{x}^{2}}+{{b}^{2}} \right)}^{3}}+{{\left( ab \right)}^{3}}\]
\[=\left( {{x}^{2}}+{{b}^{2}}+ab \right)\left\{ {{\left( {{x}^{2}}+{{b}^{2}} \right)}^{2}}-\left( {{x}^{2}}+{{b}^{2}} \right)ab+{{\left( ab \right)}^{2}} \right\}\]
\[=\left( {{x}^{2}}+{{b}^{2}}+ab \right)\left( {{x}^{4}}+2{{x}^{2}}{{b}^{2}}+{{b}^{4}}-ab{{x}^{2}}-a{{b}^{3}}+{{a}^{2}}{{b}^{2}} \right)\]
\[\left( xiv \right){{x}^{6}}+27\]
\[={{\left( {{x}^{2}} \right)}^{3}}+{{\left( 3 \right)}^{3}}\]
\[=\left( {{x}^{2}}+3 \right)\left( {{x}^{4}}-3{{x}^{2}}+9 \right)\]
\[\left( xv \right){{x}^{6}}-{{y}^{6}}\]
\[={{\left( {{x}^{3}} \right)}^{2}}-{{\left( {{y}^{3}} \right)}^{2}}\]
\[=\left( {{x}^{3}}+{{y}^{3}} \right)\left( {{x}^{3}}-{{y}^{3}} \right)\]
\[=\left( x+y \right)\left( {{x}^{2}}-xy+{{y}^{2}} \right)\left( x-y \right)\left( {{x}^{2}}+xy+{{y}^{2}} \right)\]
\[=\left( x+y \right)\left( x-y \right)\left( {{x}^{2}}-xy+{{y}^{2}} \right)\left( {{x}^{2}}+xy+{{y}^{2}} \right)\]
\[\left( xvi \right){{x}^{12}}-{{y}^{12}}\]
\[={{\left( {{x}^{6}} \right)}^{2}}-{{\left( {{y}^{6}} \right)}^{2}}\]
\[=\left( {{x}^{6}}+{{y}^{6}} \right)\left( {{x}^{6}}-{{y}^{6}} \right)\]
\[=\left\{ {{\left( {{x}^{2}} \right)}^{3}}+{{\left( {{y}^{2}} \right)}^{3}} \right\}\left\{ {{\left( {{x}^{2}} \right)}^{3}}-{{\left( {{y}^{2}} \right)}^{3}} \right\}\]
\[=\left( {{x}^{2}}+{{y}^{2}} \right)\left( {{x}^{4}}-{{x}^{2}}{{y}^{2}}+{{y}^{4}} \right)\left( {{x}^{2}}-{{y}^{2}} \right)\left( {{x}^{4}}+{{x}^{2}}{{y}^{2}}+{{y}^{4}} \right)\]
\[=\left( x+y \right)\left( x-y \right)\left( {{x}^{2}}+{{y}^{2}} \right)\left( {{x}^{4}}-{{x}^{2}}{{y}^{2}}+{{y}^{4}} \right)\left( {{x}^{4}}+{{x}^{2}}{{y}^{2}}+{{y}^{4}} \right)\]
\[\left( xvii \right){{m}^{3}}-{{n}^{3}}-m\left( {{m}^{2}}-{{n}^{2}} \right)+n{{\left( m-n \right)}^{2}}\]
\[=\left( m-n \right)\left( {{m}^{2}}+mn+{{n}^{2}} \right)-m\left( m+n \right)\left( m-n \right)+n{{\left( m-n \right)}^{2}}\]
\[=\left( m-n \right)\left\{ \left( {{m}^{2}}+mn+{{n}^{2}} \right)-m\left( m+n \right)+n\left( m-n \right) \right\}\]
\[=\left( m-n \right)\left( {{m}^{2}}+mn+{{n}^{2}}-{{m}^{2}}-mn+mn-{{n}^{2}} \right)\]
\[=mn\left( m-n \right)\]
;

