নবম শ্রেণী – ষষ্ঠ অধ্যায় : সামান্তরিকের ধর্ম সম্পূর্ণ সমাধান

কষে দেখি–6

1. প্রমাণ করি যে, একটি সামান্তরিকের কর্ণদ্বয়ের দৈর্ঘ্য সমান হলে, সামান্তরিকটি একটি আয়তাকার চিত্র।

উত্তরঃ–

ABCD সামান্তরিকের দুটি কর্ণ AC ও BD এবং AC = BD।
প্রমাণ করতে হবে যে, ABCD একটি আয়তাকার চিত্র অর্থাৎ, ∠ABC = 90°

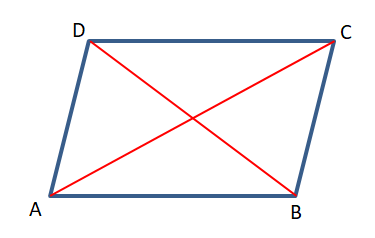
প্রমাণ – △ABC ও △ABD –এর AC = BD
AB = CD এবং AD = BC [∵ABCD সামান্তরিকের বিপরীত বাহু সমান ]
∴ △ABC ≅ △ABD [ সর্বসমতার S-S-S শর্তানুসারে ]
∴ ∠ABC = ∠BAD
আবার, ∠ABC + ∠BAD = 180°
বা, 2∠ABC = 180°
∴ ∠ABC = 90°
∴ ABCD একটি আয়তাকার চিত্র। (প্রমানিত)

2. প্রমাণ করি যে, একটি সামান্তরিকের কর্ণদ্বয়ের দৈর্ঘ্য সমান হলে এবং কর্ণদ্বয় পরস্পরকে লম্বভাবে ছেদ করলে, সামান্তরিকটি একটি বর্গাকার চিত্র।

উত্তরঃ–

ABCD সামান্তরিকের কর্ণদ্বয় AC ও BD পরস্পরকে O বিন্দুতে ছেদ করে। যার AC = BD।
প্রমাণ করতে হবে যে, ABCD বর্গাকার চিত্র।

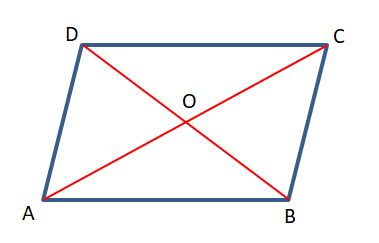
প্রমাণ – △AOB –এর ক্ষেত্রে
OA = OB ( কর্ণদ্বয় সমান এবং সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে )
∴ ∠OAB = ∠OBA
আবার, ∠AOB = 90°
∴ ∠OAB + ∠OBA = 90°
∴ ∠OAB = ∠OBA = 45°

অনুরূপভাবে, △AOD –এর ক্ষেত্রে,
∠ODA = ∠OAD = 45°
∴ ∠DAB = ∠OAD + ∠OAB = 45° + 45° = 90°
∴ ABCD একটি আয়তাকার চিত্র।

△AOB ও △BOC –এর মধ্যে তুলনা করে পাই,OA = OC
OB সাধারণ বাহু
∠AOB = ∠BOC
∴ △AOB ≅ △BOC
∴ AB = BC
∴ ABCD একটি বর্গাকার চিত্র। (প্রমানিত)

3. প্রমাণ করি যে, একটি সামান্তরিকের কর্ণদ্বয় পরস্পরকে লম্বভাবে ছেদ করলে, সামান্তরিকটি একটি রম্বস।

উত্তরঃ–

ABCD সামান্তরিকের কর্ণদ্বয় AB ও BD লম্বভাবে O বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে যে, ABCD একটি রম্বস।

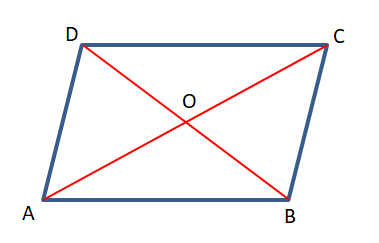
প্রমাণ – △AOB ও △BOC –এর মধ্যে
AO = OC [ সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে ]
∠AOB = ∠BOC
OB সাধারণ বাহু
∴ △AOB ≅ △BOC
∴ AB = BC
∴ ABCD একটি রম্বস। (প্রমানিত)

4. ABCD সামান্তরিকের AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করেছে। O বিন্দুগামী যেকোনো সরলরেখা AB ও DC বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে। প্রমাণ করি যে OP = OQ

উত্তরঃ–

ABCD একটি সামান্তরিক।
প্রমাণ করতে হবে যে, OP = OQ

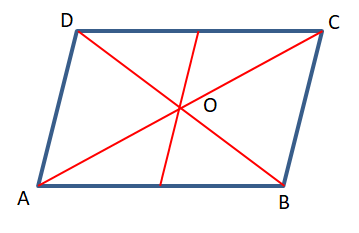
প্রমাণ – △AOP ও △COQ –এর মধ্যে
∠OAP = ∠OCQ [∵ AB∥CD ও AC ছেদক ]
∠AOP = ∠COQ [ বিপ্রতীপ কোণ ]
AO = OC [∵ ABCD সামান্তরিক ]
∴ △AOP ≅ △COQ
∴ OP = OQ (প্রমানিত)

5. প্রমাণ করি যে, একটি সমদ্বিবাহু ট্রাপিজিয়ামের যে-কোনো সমান্তরাল বাহুসংলগ্ন দুটি কোণ পরস্পর সমান।

উত্তরঃ–

ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম যার AD = BC
প্রমাণ করতে হবে যে, ∠DAB = ∠CBA
অঙ্কন – C বিন্দু থেকে অঙ্কিত DA –এর সমান্তরাল সরলরেখা AB -কে Q বিন্দুতে ছেদ করে।

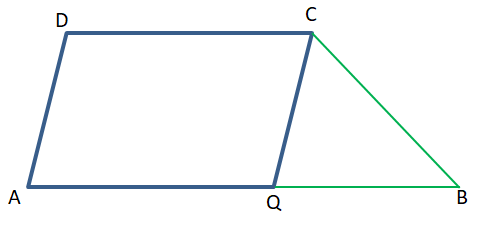
প্রমাণ – যেহেতু, AB∥DC
∴ AQ∥DC
আবার, DA∥QC∴ AQCD একটি সামান্তরিক
∴ AD = QC
আবার, AD = BC
∴ QC = BC
∴ △CQB -এর ∠CQB = ∠CBQ
∠DAQ = ∠CQB [∵ DA∥CQ ও AB ছেদক ]
∴ ∠DAQ = ∠CBQ
∴ ∠DAB = ∠CBA (প্রমানিত)

6. ABCD বর্গাকার চিত্রে BC বাহুর উপর P যে-কোনো একটি বিন্দু। B বিন্দু থেকে AP-এর উপর অঙ্কিত লম্ব DC বাহুকে Q বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, AP = BQ

উত্তরঃ–

ABCD একটি বর্গাকার চিত্র এবং ∠BOP = 90°
প্রমাণ করতে হবে যে, AP = BQ

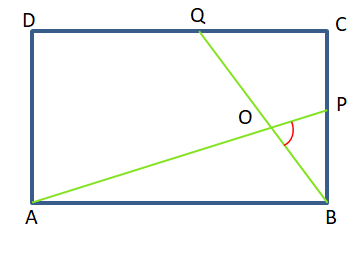
প্রমাণ – △BOP –এর ক্ষেত্রে ∠BOP = 90°
∴ ∠OBP + ∠BPO = 90° ………(1)
△BQC –এর ক্ষেত্রে ∠BCQ = 90°
∴ ∠CBQ + ∠BQC = 90°
∴ ∠OBP + ∠BQC = 90° ………(2)
(1) নং ও (2) নং থেকে ∠BQC = ∠BPO
△APB ও △BCQ –এর
∴ ∠BQC = ∠BPQ
AB = BC
∠ABC = ∠BCQ
∴ △APQ ≅ △BCQ
∴ AP = BQ (প্রমানিত)

7. প্রমাণ করি যে, একটি চতুর্ভুজের দুটি বিপরীত কোণ পরস্পর সমান ও দুটি বিপরীত বাহু পরস্পর সমান্তরাল হলে, চতুর্ভুজটি একটি সামান্তরিক।

উত্তরঃ–

ABCD একটি চতুর্ভুজ যার ∠BAD = ∠BCD, ∠ADC = ∠ABC, AB∥DC এবং DA∥BC
প্রমাণ করতে হবে যে, ABCD একটি সামান্তরিক।
অঙ্কন – AC কর্ণ অঙ্কন করলাম।

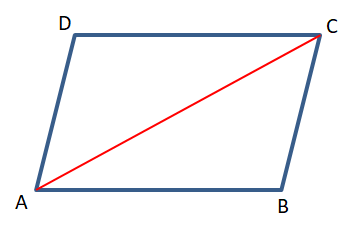
প্রমাণ – △ABC ও △ACD –এর মধ্যে তুলনা করে পাই,
∠BAC = একান্তর ∠ACD [∵ AB∥DC ও AC ছেদক ]
∠DAC = একান্তর ∠ACB [∵ DA∥BC ও AC ছেদক ]
AC সাধারণ বাহু
∴ △ABC ≅ △ACD
∴ AB = DC
আবার, AB∥DC
∴ ABCD একটি সামান্তরিক। (প্রমানিত)

8. ∆ABC-এর BP ও CQ মধ্যমা দুটি যথাক্রমে R ও S বিন্দু পর্যন্ত এমনভাবে বর্ধিত করা হল যে, BP = PR এবং CQ = QS হয়। প্রমাণ করি যে, S, A, R বিন্দু তিনটি সমরেখ।

উত্তরঃ–

∆ABC-এর BP ও CQ মধ্যমা দুটি যথাক্রমে R ও S বিন্দু পর্যন্ত এমনভাবে বর্ধিত করা হল যে,BP = PR এবং CQ = QS হয়।
প্রমাণ করতে হবে যে, S, A, R বিন্দু তিনটি সমবিন্দু।
অঙ্কন – S, A; A, R বিন্দুগুলি যোগ করি ও S, B; C, R বিন্দুগুলি যোগ করি।

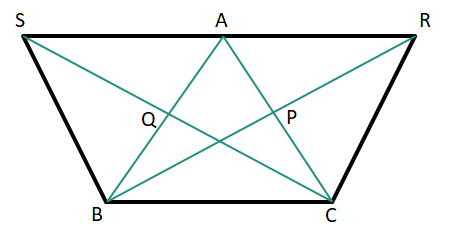
প্রমাণ – ACBS চতুর্ভুজের BQ = AQ, CQ = QS
∴ ACBS চতুর্ভুজের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে।
∴ ACBS একটি সামান্তরিক
∴ SA = BC এবং SA∥BC

অনুরূপভাবে, ABCR ও একটি সামান্তরিক।
∴ AR = BC, AR∥BC
∴ SA = AR এবং SR∥BC
∴ S, A, R বিন্দু তিনটি সমরেখ। (প্রমানিত)

9. PQRS সামান্তরিকের SQ কর্ণ K ও L বিন্দুতে সমান তিনভাগে বিভক্ত হয়েছে। PK, SR-কে M বিন্দুতে এবং RL, PQ কে N বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, PMRN একটি সামান্তরিক।

উত্তরঃ–

PQRS সামান্তরিকের SQ কর্ণ K ও L বিন্দুতে সমান তিনভাগে বিভক্ত হয়েছে। PK, SR-কে M বিন্দুতে এবং RL, PQ কে N বিন্দুতে ছেদ করেছে। SK = KL = LQ
প্রমাণ করতে হবে যে, PMRN একটি সামান্তরিক।

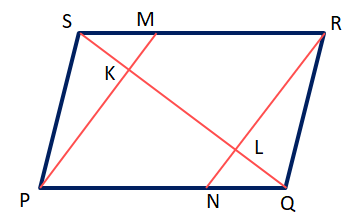
প্রমাণ – △PKS ও △RLQ -এর
SK = LQ
SP = RQ
∠PSK = একান্তর ∠LQR [∵ SR∥PQ এবং SQ ছেদক ]
∴ △PKS ≅ △RLQ
∴ PK = RL ………(1)
এবং ∠SPK = ∠LRQ ………(2)

△PSM ও △RNB –এর
SP = RQ
∠PSM = ∠RQN
∠SPM = ∠NRQ [ (2) নং থেকে পাই ]
∴ △PSM ≅ △RNQ
∴ SM = NQ
∵ SR = PQ
∴ SM + MR = PN + NQ
∴ MR = PN

আবার, PQRS সামান্তরিকের SR∥PQ
∴ MR∥PN
∴ PMRN চতুর্ভুজের MR = PN এবং MR∥PN
∴ PMRN একটি সামান্তরিক। (প্রমানিত)

10. ABCD ও AECF দুটি সামান্তরিকেরই AC একটি কর্ণ। B, E, D, F বিন্দুগুলি সমরেখ না হলে, প্রমাণ করি যে, BEDF একটি সামান্তরিক।

উত্তরঃ–

ABCD ও AECF দুটি সামান্তরিকেরই AC একটি কর্ণ।
প্রমাণ করতে হবে যে, BEDF একটি সামান্তরিক।
অঙ্কন – ABCD সামান্তরিকের BD কর্ণ ও AECF সামান্তরিকের EF কর্ণ অঙ্কন করা হল। সামান্তরিকের কর্ণদ্বয় O বিন্দুতে ছেদ করে।

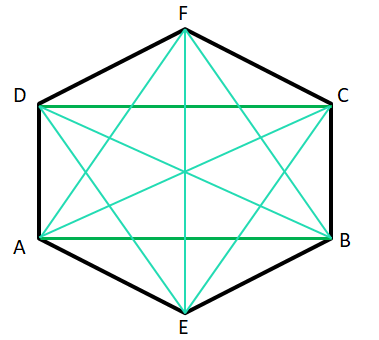
প্রমাণ – যেহেতু, ABCD সামান্তরিকের AC ও BD কর্ণ
OA = OC এবং OB = OD ………(1)
যেহেতু, AECF সামান্তরিকের AC ও EF কর্ণ
OA = OC এবং OE = OF ………(2)
BEDF চতুর্ভুজের BD ও EF কর্ণ OB = OD [ (1) থেকে পাই ]
OE = OF [(2) থেকে পাই ]
∴ BEDF চতুর্ভুজের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে।
∴ BEDF একটি সামান্তরিক।(প্রমানিত)

11. ABCD একটি চতুর্ভুজ। ABCE ও BADF দুটি সামান্তরিক অঙ্কন করা হলো। প্রমাণ করি যে, CD ও EF পরস্পরকে সমদ্বিখণ্ডিত করে।

উত্তরঃ–

ABCD একটি চতুর্ভুজ। ABCE ও BADF দুটি সামান্তরিক।
প্রমাণ করতে হবে যে, CD ও EF পরস্পরকে সমদ্বিখণ্ডিত করে।
অঙ্কন – D, E এবং C, F যুক্ত করা হল।

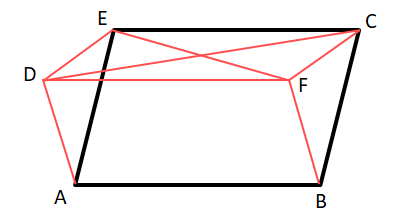
প্রমাণ – DFCE চতুর্ভুজের
DF = CE [∵ ABCE সামান্তরিকের AB = CE, BADF সামান্তরিকের AB = DF]
DF∥CE [∵ ABCE সামান্তরিকের AB∥CE, BADE সামান্তরিকের AB∥DF]
∴ DFCE চতুর্ভুজের একজোড়া বিপরীত বাহু সমান এবং সমান্তরাল।
DFCE একটি সামান্তরিক।
আবার, CD ও EF হল DFCE সামান্তরিকের কর্ণ।
∴ CD ও EF পরস্পরকে সমদ্বিখণ্ডিত করে। (প্রমানিত)

12. ABCD সামান্তরিকের AB = 2 AD; প্রমাণ করি যে ∠BAD ও ∠ABC -এর সমদ্বিখণ্ডদ্বয় DC বাহুর মধ্যবিন্দুতে সমকোণে মিলিত হয়।

উত্তরঃ–

মনেকরি, ABCD সামান্তরিকের ∠BAD ও ∠ABC –এর সমদ্বিখন্ডকদ্বয় DC বাহুকে E বিন্দুতে ছেদ করে। AB = 2AD।
প্রমাণ করতে হবে যে, (i) DE = EC এবং (ii) ∠AEB = 90°
অঙ্কন – E বিন্দু এবং AB বাহুর মধ্যবিন্দু P যুক্ত করা হল।

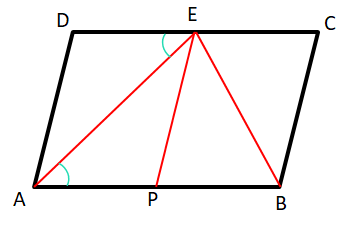
প্রমাণ – △DAE ও △APE –এর
AD = AP [∵ AB = 2AD এবং AB = 2AP]
∠PAE = একান্তর ∠AED [∵ AB∥CD এবং AE ছেদক ]AE সাধারণ বাহু।
∴ DAE ≅ APE∴ DE = PE
অনুরূপভাবে, EC = PE
∴ DE = EC ……..(i) (প্রমানিত)
∴ ABCD একটি সামান্তরিক।
∠DAB + ∠ABC = 180°
∴ ½ ∠DAB + ½ ∠ABC = 90°
∴ ∠EAB + ∠EBA = 90°
∴ ∠AED + ∠BEC = 90°
∴ ∠AEB = 180° – (∠AED + ∠BEC) = 180° – 90°
∴ ∠AEB = 90° ………(ii) (প্রমানিত)

13. ABCD সামান্তরিকের AB ও AD বাহুর উপর যথাক্রমে ABPQ ও ADRS বর্গাকার চিত্র অঙ্কন করা হলো যারা সামান্তরিকটির বাইরে অবস্থিত। প্রমাণ করি যে, PRC ত্রিভুজটি সমদ্বিবাহু।

উত্তরঃ–

ABCD সামান্তরিকের AB ও AD বাহুর উপর যথাক্রমে ABPQ ও ADRS বর্গাকার চিত্র।
প্রমাণ করতে হবে যে, PRC একটি সমদ্বিবাহু ত্রিভুজ।

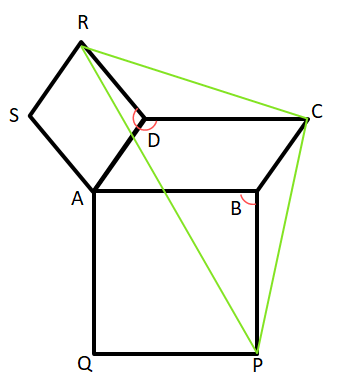
প্রমাণ – ABCD একটি সামান্তরিক
∠ADC = ∠ABC
∴ ABPQ ও ADRS বর্গাকার চিত্র,
∠ADR = ∠ABP = 90°
∴ ∠RDC + ∠ADC + ∠ADR = ∠CBP + ∠ABP + ∠ABC
∴ ∠RDC = ∠CBP ………(1)
আবার, AB = CD [∵ ABCD সামান্তরিক ]
AB = BP [ ABPQ বর্গাকার ]
∴ BP = CD
অনুরূপভাবে, CB = CD
△RDC ও △PBC –এর
BP = CD
CB = RD
∠RDC = ∠CBP
∴ △RDC = △PBC
∴ RC = PC
∴ △PRC –এর RC = PC
∴ △PRC একটি সমদ্বিবাহু ত্রিভুজ। (প্রমানিত)

14. ABCD সামান্তরিকের ∠BAD স্থূলকোণ; AB ও AD বাহুর উপর দুটি সমবাহু ত্রিভুজ ABP ও ADQ অঙ্কন করা হলো যারা সামান্তরিকের বাইরে অবস্থিত। প্রমাণ করি যে, CPQ একটি সমবাহু ত্রিভুজ।

উত্তরঃ–

ABCD সামান্তরিকের ÐBAD স্থূলকোণ; AB ও AD বাহুর উপর দুটি সমবাহু ত্রিভুজ ABP ও ADQ।
প্রমাণ করতে হবে যে, CBQ একটি সমবাহু ত্রিভুজ।

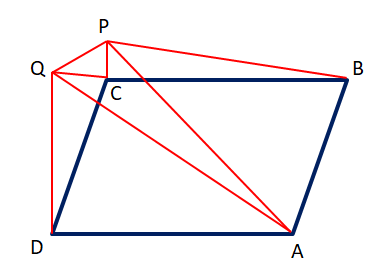
প্রমাণ – △DQC ও △PCB –এর
DC = PB [∵ DC = AB, AB = PB]
QD = BC [∵ QA = DA, DA = BC]
∠QDC = ∠PBC [∵ ∠QDA = ∠PBA = 60°]
∠QDC + ∠CDA = ∠PBC + ∠CBA
∴ ∠QDC = ∠PBC [∵ ∠CDA = ∠CBA]
∴ △DQC ≅ △PCB
∴ CQ = PC ……..(1)
△CDQ ও △PQA –এর
QD = QA [∵ DQA সমবাহু ত্রিভুজ ]
CD = PD [∵ CD = AB, AB = PA]
∠CDQ = ∠QAP [∵ ∠CDA + ∠BAD = 180° বা, 60° – ∠CDQ + 60° + ∠QPA + 60° = 180° ]
∴ △CDQ ≅ △PQA
∴ CQ = QP ………(2)
(1) নং ও (2) নং থেকে পাই, CQ = QP = PC
∴ △CPQ –এর CQ = QP = PC
∴ △CPQ একটি সমবাহু ত্রিভুজ। (প্রমানিত)

15. OP, OQ ও OR তিনটি সরলরেখাংশ। OPAQ, OQBR এবং ORCP সামান্তরিক তিনটি অঙ্কন করা হলো। প্রমাণ করি যে, AR , BP ও CQ পরস্পরকে সমদ্বিখণ্ডিত করে।

উত্তরঃ–

OP, OQ ও OR তিনটি সরলরেখাংশ। OPAQ, OQBR এবং ORCP সামান্তরিক।
প্রমাণ করতে হবে যে, AR, BP ও CQ পরস্পরকে সমদ্বিখন্ডিত করে।
অঙ্কন – Q, R ও A, C যুক্ত করা হল। Q, P ও B, C যুক্ত করা হল।

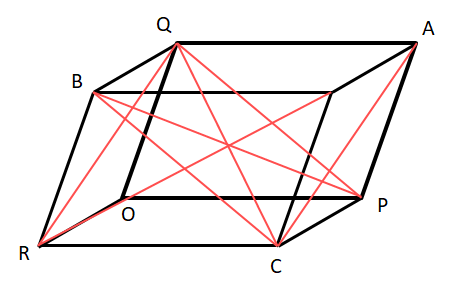
প্রমাণ – AQRC চতুর্ভুজের
QA∥RC [∵△PAQ সামান্তরিকের QA∥OP এবং OPCR সামান্তরিকের OP∥RC]
QA = RC [∵ QA = OP, OP = RC]
∴ AQRC একটি সামান্তরিক।
আবার, AQRC সামান্তরিকে AR ও CQ দুটি কর্ণ।
∴ AR, CQ পরস্পরকে সমদ্বিখন্ডিত করে।
BCPQ চতুর্ভুজের
BQ∥CP [∵ ORCP সামান্তরিকের CP∥OR এবং OQBR সামান্তরিকে OR∥BQ]
BQ = CP [∵ CP = OR, OR = BQ]
∴ BCPQ সামান্তরিক।
আবার, BCPQ সামান্তরিকে BP, CQ দুটি কর্ণ।
∴ BP, CQ পরস্পরকে সমদ্বিখন্ডিত করে।
∴ AR, BP, CQ পরস্পরকে সমদ্বিখন্ডিত করে। (প্রমানিত)

16. বহু বিকল্পীয় প্রশ্ন (M. C.Q.):

(i) ABCD সামান্তরিকের ∠BAD = 75° এবং ∠CBD = 60° হলে, ∠BDC-এর পরিমাপ

(a) 60° (b) 75° (c) 45° (d) 50°

উত্তরঃ-

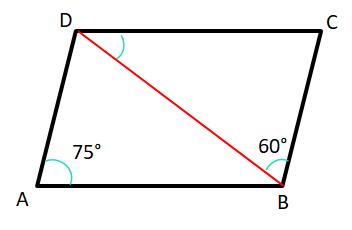
∠BAD = 75°
∴ ∠ABC = 180° – 75° = 105°
∴ ∠ABD = 105° – 60° = 45°
∴ ∠BDC = 45°
∴ সঠিক উত্তরটি হল – (c) 45°

(ii) নিম্নলিখিত জ্যামিতিক চিত্রগুলির কোনটির কর্ণদ্বয়ের দৈর্ঘ্য সমান তা লিখি।

(a) সামান্তরিক (b) রম্বস (c) ট্রাপিজিয়াম (d) আয়তাকার চিত্র

উত্তরঃ–

∴ সঠিক উত্তরটি হল – (d) আয়তাকার চিত্র

(iii) ABCD সামান্তরিকের ∠BAD= ∠ABC হলে, ABCD সামান্তরিকটি

(a) রম্বস (b) ট্রাপিজিয়াম (c) আয়তাকার চিত্র (d) কোনোটিই নয়

উত্তরঃ–

∴ সঠিক উত্তরটি হল – (c) আয়তাকার চিত্র

(iv) ABCD সামান্তরিকের BD কর্ণের মধ্যবিন্দু M; BM, ∠ABC-কে সমদ্বিখণ্ডিত করলে, ∠AMB এর পরিমাপ।

(a) 45° (b) 60° (c) 90° (d) 75°

উত্তরঃ-

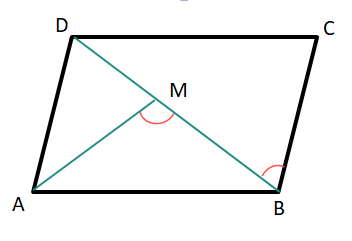
∠DAB + ∠ABC = 180°
∴ ½ ∠DAB + ½ ∠ABC = 90°
∴ ∠MAB + ∠MBA = 90°
∴ ∠AMB = 90°
∴ সঠিক উত্তরটি হল – (c) 90°

(v) ABCD রম্বসের ∠ACB=40° হলে, ∠ADB – এর পরিমাপ

(a) 50° (b) 110° (c) 90° (d) 120°

উত্তরঃ-

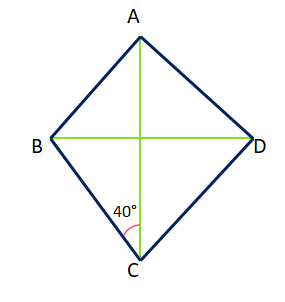
∠ACB = 40°
∴ ∠CBD = 50°
∴ ∠CBD = ∠ADB [∵ AB∥CD BD]
∴ ∠ADB = 50°
∴ সঠিক উত্তরটি হল – (a) 50°

17. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন:

(i) ABCD সামান্তরিকের ∠A:∠B = 3:2 হলে, সামান্তরিকটির কোণগুলির পরিমাপ লিখি।

উত্তরঃ-

মনেকরি, ∠A = 3x°, ∠B = 2x°
∠A + ∠B = 180°
বা, 3x° + 2x° = 180°
বা, 5x° = 180°
বা, x° = 36°
∴ ∠A = 3 × 36° = 108° = ∠C
∴ ∠B = 2 × 36° = 72° = ∠D

(ii) ABCD সামান্তরিকের ∠A ও ∠B-এর সমদ্বিখণ্ডদ্বয় CD বাহুর উপর E বিন্দুতে মিলিত হয়। BC বাহুর দৈর্ঘ্য 2 সেমি. হলে, AB বাহুর দৈর্ঘ্য কত তা লিখি।

উত্তরঃ-

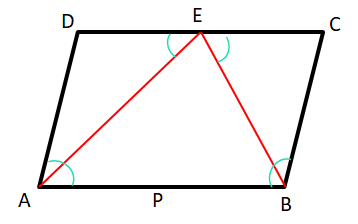
যেহেতু, ABCD একটি সামান্তরিক।
∠DAB + ∠ABC = 180°
বা, ½ ∠DAB + ½ ∠ABC = 90°
বা, ∠EAB + ∠EBA = 90°
∴ ∠AEB = 90°
∴ ABCD সামান্তরিকের ∠A ও ∠B –এর সমদ্বিখন্ডকদ্বয় CD বাহুর উপর E বিন্দুতে সমকোণে মিলিত হয়।
∴ AB = 2AD = 2 × 2 = 4 সেমি।

(iii) ABCD বর্গাকার চিত্রের ভিতর সমবাহু ত্রিভুজ AOB অবস্থিত। ∠COD -এর পরিমাপ লিখি।

উত্তরঃ-

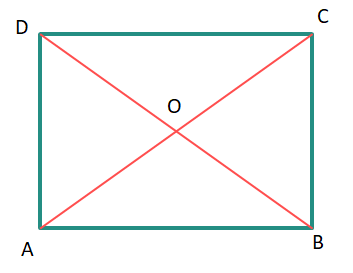
এখানে, △AOB একটি সমবাহু ত্রিভুজ।
∴ OA = AB = OB
∴ ∠AOD = ∠ADO
আবার, ∠OAB = ∠AOB = ∠OBA = 60°
△AOD –এর ক্ষেত্রে
OA = AD [∵ OA = AB, AB = DA]
∴ ∠AOD = ∠ADO
∴ ∠DAB = 90°, ∠OAB = 60°
∴ ∠OAD = 90° – 60° = 30°
∴ ∠AOD + ∠ADO = 180° – 30° = 150°
∴ ∠ADO = \frac{150{}^\circ }{2}=75{}^\circ
∴ ∠ADC = 90°
∴ ∠ODC = 90° – 75° = 15°
অনুরূপভাবে, ∠OCD = 15°
∴ ∠COD = 180° – (∠ODC + ∠OCD) = 180° – (15° + 15°) = 180° – 30° = 150°

(iv) ABCD বর্গাকার চিত্রের AD বাহুর উপর M একটি বিন্দু যাতে ∠CMD = 30° হয়। কর্ণ BD, CM-কে P বিন্দুতে ছেদ করলে, ∠DPC-এর পরিমাপ কত তা লিখি।

উত্তরঃ-

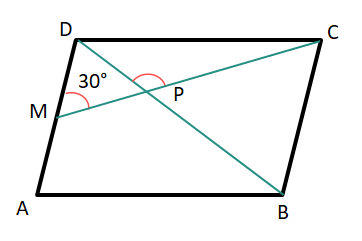
∠ADB = \frac{90{}^\circ }{2}=45{}^\circ
∴ ∠CPD = ∠CMD + ∠ADB = 30° + 45° = 75°

(v) ABCD রম্বসের AB বাহুর দৈর্ঘ্য 4 সেমি. এবং ∠BCD = 60° হলে, কর্ণ BD -এর দৈর্ঘ্য কত তা লিখি।

উত্তরঃ-

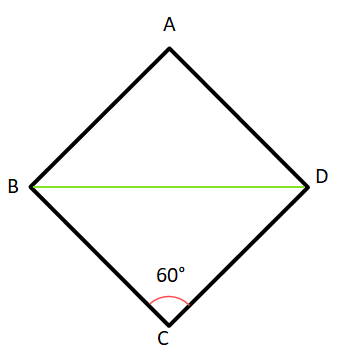
ABCD একটি রম্বস।
∴ AB = BC = CD = DA = 4 সেমি.
∵ △BCD –এর ক্ষেত্রে BC = CD
∴ ∠CBD = ∠CDB
∠BCD = 60°
∴ ∠CBD = ∠CDB = 60°
∴ ABCD একটি সমবাহু ত্রিভুজ।
∴ কর্ণ BD –এর দৈর্ঘ্য 4 সেমি.।

;