কষে দেখি – 6
1. মনে মনে ভাবি ও লিখি :
(a) দুটি সূক্ষ্মকোণ পরস্পর পূরক হতে পারে কিনা লিখি।
(b) দুটি সূক্ষ্মকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি।
(c) একটি সূক্ষ্মকোণ ও একটি স্থুলকোণ পরস্পর পূরক হতে পারে কিনা লিখি। দুটি সমকোণ পরস্পর পূরক হতে পারে কিনা লিখি।
(d) দুটি স্থুলকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি।
(e) দুটি সমকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি।
(f) একটি সূক্ষ্মকোণ ও একটি স্থুলকোণ পরস্পর সম্পূরক হতে পারে কিনা লিখি।
(g) দুটি সন্নিহিত কোণ পরস্পর পূরক কোণ হতে পারে কিনা লিখি।
(h) দুটি সন্নিহিত কোণ পরস্পর সম্পূরক কোণ হতে পারে কিনা লিখি।
উত্তরঃ-
(a) দুটি সূক্ষ্মকোণ পরস্পর পূরক হতে পারে।
(b) দুটি সূক্ষ্মকোণ পরস্পর সম্পূরক হতে পারে না।
(c) একটি সূক্ষ্মকোণ ও একটি স্থুলকোণ পরস্পর পূরক হতে পারে না। দুটি সমকোণ পরস্পর পূরক হতে পারে না।
(d) দুটি স্থুলকোণ পরস্পর সম্পূরক হতে পারে না।
(e) দুটি সমকোণ পরস্পর সম্পূরক হতে পারে।
(f) একটি সূক্ষ্মকোণ ও একটি স্থুলকোণ পরস্পর সম্পূরক হতে পারে।
(g) দুটি সন্নিহিত কোণ পরস্পর পূরক হতে পারে।
(h) দুটি সন্নিহিত কোণ পরস্পর সম্পূরক হতে পারে।
2. নীচের সন্নিহিত কোণগুলি আঁকি ও কোন কোণগুলি পরস্পর পূরক অথবা সম্পূরক লিখি :
45°, 45°; 120°, 30°; 70°, 110°; 42°, 48°; 37°, 43°; 85°, 95°;
উত্তরঃ-
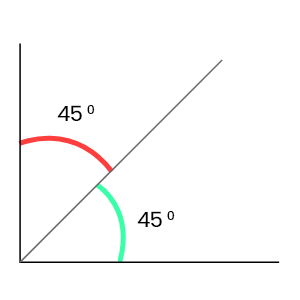
45° + 45° = 90°
∴ পরস্পর পূরক কোণ।
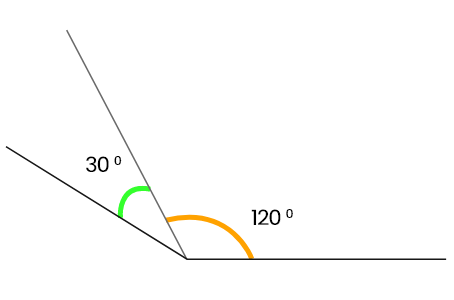
120° + 30° = 150°
∴ 120° ও 30° সন্নিহিত কোণ দুটি মিলে মোট 150° কোণ তৈরি হয়েছে। সুতরাং, এরা পরস্পর পূরক বা সম্পূরক কোণ নয়।
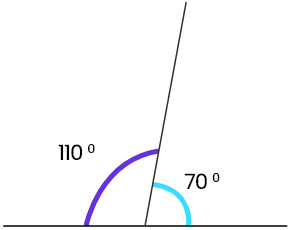
70° + 110° = 180°
∴ 70° ও 110° সন্নিহিত কোণ দুটি মিলে মোট 180°কোণ তৈরি হয়েছে। সুতরাং, এরা পরস্পর সম্পূরক কোণ।
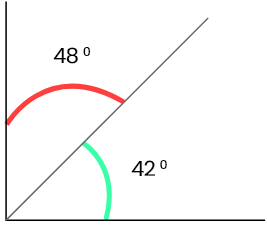
42° + 48° = 90°
∴ 42° ও 48° সন্নিহিত কোণ দুটি মিলে মোট 90°কোণ তৈরি হয়েছে। সুতরাং, এরা পরস্পর পূরক কোণ।
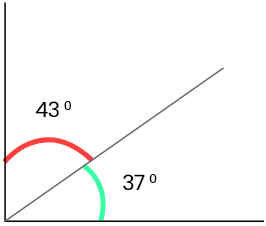
37° + 43° = 90°
∴ 37° ও 43° সন্নিহিত কোণ দুটি মিলে মোট 90°কোণ তৈরি হয়েছে। সুতরাং, এরা পরস্পর পূরক কোণ।
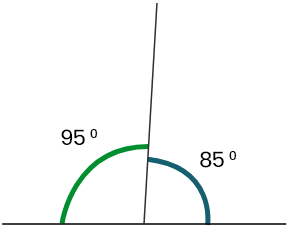
85° + 95° = 180°
∴ 85° ও 95° সন্নিহিত কোণ দুটি মিলে মোট 180°কোণ তৈরি হয়েছে। সুতরাং, এরা পরস্পর সম্পূরক কোণ।
3. নীচের কোণগুলি দেখি ও কোন কোন কোণদুটি পরস্পর পূরক কোণ লিখি ;
31°, 47°, 64°, 29°, 43°, 59°, 17°, 26°
উত্তরঃ-
31° এর পূরক কোণ = 90° – 31° = 59°
47° এর পূরক কোণ = 90° – 47° = 43°
64° এর পূরক কোণ = 90° – 64° = 26°
29° এর পূরক কোণ = 90° – 29° = 61°
∴ পরস্পরের পূরক কোণগুলি –
(31°, 59°), (47°, 43°) (64°, 26°)
4. নীচের কোণগুলি দেখি ও কোন কোন কোণগুলি পরস্পর সম্পূরক কোণ লিখি :
47°, 58°, 69°, 75°, 133°, 105°, 122°, 125°
উত্তরঃ-
47° এর সম্পূরক কোণ = 180° – 47° = 133°
58° এর সম্পূরক কোণ = 180° – 58° = 122°
69° এর সম্পূরক কোণ = 180° – 69° = 111°
75° এর সম্পূরক কোণ = 180° – 75° = 105°
∴ পরস্পরের সম্পূরক কোণগুলি –
(47°, 133°), (58°, 122°) (75°, 105°)
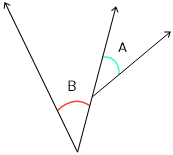
5. সন্নিহিত কোণ কাকে বলে লিখি ও নীচের কোন কোণগুলি সন্নিহিত কোণ বুঝে লিখি :
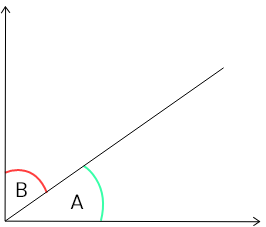 |  |  |  |
উত্তরঃ-
যখন দুটি কোণের শীর্ষবিন্দু একই ও কোণ দুটি একই সাধারণ বাহুর দুপাশে অবস্থিত হয় তখন ওই কোণ দুটিকে সন্নিহিত কোণ বলা হয়।
প্রশ্নের প্রথম, দ্বিতীয় ও তৃতীয় ছবি তিনটি সন্নিহিত কোণের ছবি। কারণ এই তিনটি ছবির প্রত্যেকটির শীর্ষবিন্দু এক এবং একই সাধারণ বাহুর দুপাশে অবস্থিত A ও B কোণ দুটি।
কিন্তু চতুর্থ ছবিটির কোণ দুটি সন্নিহিত কোণ নয়; কারণ A ও B কোণের শীর্ষবিন্দু পৃথক।
6. নিজে চাঁদার সাহায্যে সন্নিহিত কোণ আঁকি যার কোণদুটির মান হলো
35°, 45°; 18°, 42°; 32°,90°; 73°,63°
উত্তরঃ-
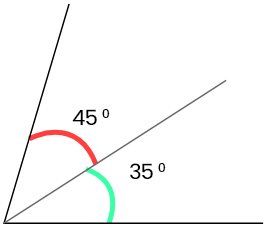 |  |
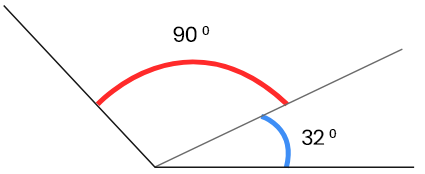 |  |
7. সায়ন্তনী একটি সরলরেখা AB আঁকল। আমি সেই সরলরেখার উপর কোনো বিন্দু P-তে অপর একটি রশ্মি PQ আঁকলাম। এর ফলে দুটি সন্নিহিত কোণ \angle BPQ ও \angle APQ তৈরি হলো। চাঁদার সাহায্যে মেপে \angle BPQ ও \angle APQ এর পরিমাপ লিখি ও \angle BPQ+\angle APQ = কত লিখি।
উত্তরঃ-
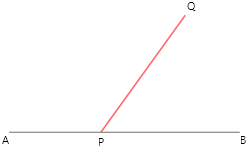
\[\angle BPQ=50{}^\circ \]
\[\angle APQ=130{}^\circ \]
\[\angle BPQ+\angle APQ\]
\[=50{}^\circ +130{}^\circ \]
\[=180{}^\circ \]
8. শাকিল দুটি সন্নিহিত কোণ \angle ABC ও \angle ABD আঁকল যাদের সমষ্টি 180°; আমিও শাকিলের মত \angle ABC ও \angle ABD এঁকে দেখি D, B ও C বিন্দু তিনটি একই সরলরেখায় আছে কিনা।
উত্তরঃ-
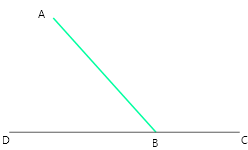
প্রদত্ত চিত্রে
\[\angle ABC+\angle ABD=180{}^\circ \]
D, B ও C বিন্দু তিনটি একই সরলরেখায় আছে।
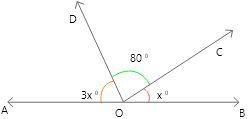
9. ছবি থেকে x -এর মান নির্ণয় করি।
উত্তরঃ-
AB সরলরেখাংশের উপর একটি বিন্দু O এবং O বিন্দু থেকে নির্গত দুটি রশ্মি OC ও OD
\[\therefore \angle BOC+\angle COD+\angle DOA=180{}^\circ \]
\[\Rightarrow x{}^\circ +80{}^\circ +3x{}^\circ =180{}^\circ \]
\[\Rightarrow 4x{}^\circ +80{}^\circ =180{}^\circ \]
\[\Rightarrow 4x{}^\circ =180{}^\circ -80{}^\circ \]
\[\Rightarrow 4x{}^\circ =100{}^\circ \]
\[\Rightarrow x{}^\circ =\frac{100{}^\circ }{4}\]
\[\Rightarrow x{}^\circ =25{}^\circ \]
\[\therefore x=25\]
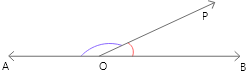
10. ছবিতে \angle AOP, \angle BOP -এর চেয়ে 140° বেশি। \angle AOP ও \angle BOP -এর মান নির্ণয় করি।
উত্তরঃ-
ধরি, \angle BOP=x^\circ
\[\therefore \angle AOP=140{}^\circ +x{}^\circ \]
AB সরলরেখার উপর O বিন্দু থেকে OP রশ্মি নির্গত হয়েছে।
\[\therefore \angle AOP+\angle BOP=180{}^\circ \]
\[\Rightarrow \left( 140{}^\circ +x{}^\circ \right)+x{}^\circ =180{}^\circ \]
\[\Rightarrow 140{}^\circ +x{}^\circ +x{}^\circ =180{}^\circ \]
\[\Rightarrow 2x{}^\circ =180{}^\circ -140{}^\circ \]
\[\Rightarrow 2x{}^\circ =40{}^\circ \]
\[\Rightarrow x{}^\circ =\frac{40{}^\circ }{2}\]
\[\therefore \angle BOP=x{}^\circ =20{}^\circ \]
\[\angle AOP=140{}^\circ +20{}^\circ =160{}^\circ \]
11. দুটি সন্নিহিত কোণের মান 35° ও 145°; সন্নিহিত কোণের বহিঃস্থ বাহু দুটি কীভাবে অবস্থিত লিখি।
উত্তরঃ-
দুটি সন্নিহিত কোণের মান 35° ও 145°
∴ সন্নিহিত কোণদুটির মোট মান 35° + 45° = 180°
দুটি সন্নিহিত কোণের সমষ্টি 180° হলে সন্নিহিত কোণের বাহু দুটি একই সরলরেখায় অবস্থিত হবে।
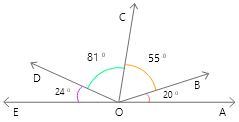
12. ছবিতে OA ও OE কীভাবে অবস্থিত লিখি।
উত্তরঃ-
\[\angle AOB+\angle BOC+\angle COD+\angle DOE=\angle AOE\]
\[\Rightarrow 20{}^\circ +55{}^\circ +81{}^\circ +24{}^\circ =\angle AOE\]
\[\Rightarrow 180{}^\circ =\angle AOE\]∴ OA ও OE একই সরলরেখায় অবস্থিত।
;

