অষ্টম শ্রেণি – অষ্টম অধ্যায় : সমান্তরাল সরলরেখা ও ছেদকের ধর্ম সম্পূর্ণ সমাধান

কষে দেখি – 8.1

1. চন্দ্রা লাইন টানা খাতার পাতা নিল। দুটি লাইনের মাঝে একটি ছেদক টানল। এর ফলে 4 জোড়া অনুরূপ কোণ, 2 জোড়া একান্তর কোণ ও 2 জোড়া একই পাশের অন্তঃস্থ কোণ তৈরি হলো। তাদের খুঁজে নাম দিই ও লিখি। চাঁদার সাহায্যে মেপে যাচাই করি যে,
          i)অনুরূপ কোণগুলি পরস্পর সমান
          ii) একান্তর কোণগুলি পরস্পর সমান
          iii)একই পাশের অন্তঃস্থ কোণগুলি পরস্পর সম্পূরক

উত্তরঃ-

a ও b খাতার পাতার দুটি লাইন। l এই দুটি লাইনের মাঝে একটি ছেদক। এর ফলে 4 জোড়া অনুরূপ কোণ তৈরি হল। যথা – (∠1, ∠5); (∠2, ∠6); (∠4, ∠8) ও (∠3, ∠7)
2 জোড়া একান্তর কোণ, যথা –  (∠4, ∠6) ও (∠3, ∠5)
2 জোড়া একই পাশের অন্তঃস্থ কোণ, যথা – (∠4, ∠5) এবং (∠3, ∠6)

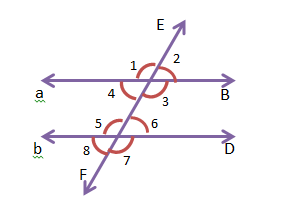
চাঁদার সাহায্যে মেপে দেখা হল –

কোণ	কোণের  ধরন	কোণগুলির পরিমাপ	সমান/ সম্পূরক	সিদ্ধান্ত
∠1, ∠5 ∠2, ∠6 ∠4, ∠8 ∠3, ∠7	অনুরূপ কোণ অনুরূপ কোণ অনুরূপ কোণ অনুরূপ কোণ	∠1 = 110°, ∠5 = 110° ∠2 = 70°, ∠6 = 70° ∠4 = 70°, ∠8 = 70° ∠3 = 110°, ∠7 = 110°	∠1 = ∠5 ∠2 = ∠6 ∠4 = ∠8 ∠3 = ∠7	অনুরূপ কোণ গুলি পরস্পর সমান
∠4, ∠6 ∠3, ∠5	একান্তর কোণ একান্তর কোণ	∠4 = 70°, ∠6 = 70° ∠3 = 110°, ∠5 = 110°	∠4 = ∠6 ∠3 = ∠5	একান্তর কোণ গুলি পরস্পর সমান
∠4, ∠5   ∠3, ∠6	ছেদকের একই পাশের অন্তঃস্থ কোণ ছেদকের একই পাশের অন্তঃস্থ কোণ	∠4 = 70°, ∠5 = 110°   ∠3 = 110°, ∠6 = 70°	∠4 + ∠5 = 180° (সম্পূরক) ∠3 + ∠6 = 180° (সম্পূরক)	ছেদকের একই পাশের অন্তঃস্থ কোণগুলি পরস্পর সম্পূরক ।

2. পাশের ছবির কোণগুলি দেখি ও কোনগুলি অনুরূপ কোণ, কোনগুলি একান্তর কোণ ও কো1f7e7bনগুলি একই পাশের অন্তঃস্থ কোণ লিখি।

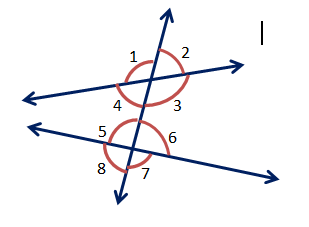
উত্তরঃ-

অনুরূপ কোণ – (∠1, ∠5); (∠2, ∠6); (∠4, ∠8) ও (∠3, ∠7)
একান্তর কোণ – (∠4, ∠6) ও (∠3, ∠5)
একই পাশের অন্তঃস্থ কোণ – (∠4, ∠5) এবং (∠3, ∠6)

3. AB||CD হলে নীচের কোণগুলির মান লিখি—

(a)	(b)	(c)
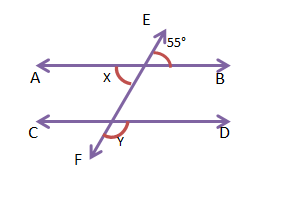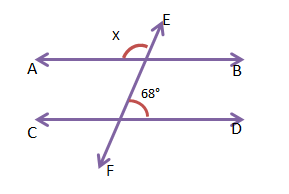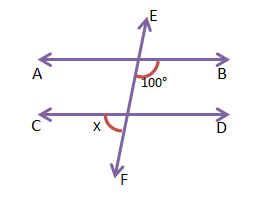X=_____, Y=_____	X=_____	X=_____

উত্তরঃ-

(a) x = 55°, y = 125°
(b) x = 112°
(c) x = 110°

4. পাশের ছবির XY||PQ হলে 7 টি কোণের মান লিখি।

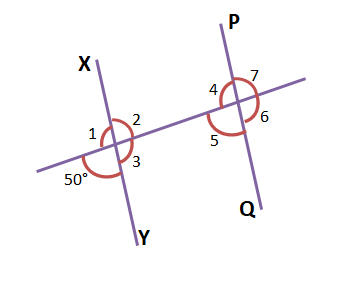
উত্তরঃ-

∠1 = 180° – 50° = 130°
∠2 = 50° [ বিপ্রতীপ কোণের সমান ]
∠3 = ∠1 = 30° [ বিপ্রতীপ কোণ ]
∠4 = ∠1 = 30° [ অনুরূপ কোণ ]
∠5 = 50° [ অনুরূপ কোণের সমান ]
∠6 = ∠3 = 30° [ অনুরূপ কোণ ]

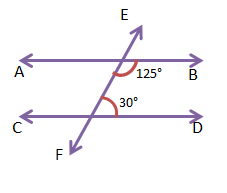
5. নীচের AB ও CD সরলরেখা দুটি সমান্তরাল কিনা কোণের মান দেখে যুক্তি দিয়ে লিখি—

(i)	(ii)	(iii)

উত্তরঃ-

(i)  AB ও CD দুটি সরলরেখা এবং EF তাদের ছেদক। সরলরেখাদ্বয়ের ছেদকের একই পাশে উৎপন্ন কোণ দুটির সমষ্টি 180° হলে সরলরেখা দুটি পরস্পর সমান্তরাল হয়।
কিন্তু এখানে 125° + 30° = 155° ≠ 180°
∴ AB ও CD সরলরেখা দুটি সমান্তরাল নয়।

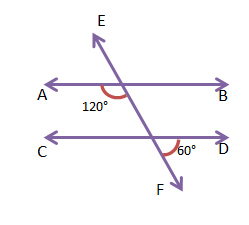
(ii) 60°-এর বিপ্রতীপ কোণ = 60°
120° + 60° = 180°
∴ AB ও CD সরলরেখা দুটির ছেদক EF-এর একই পাশের অন্তঃস্থ কোণ দুটির সমষ্টি 180°।
সুতরাং, AB || CD

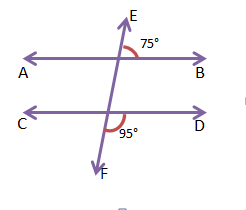
(iii) 180° – 95° = 85°
AB ও CD সরলরেখা দুটির ছেদক EF দুটি অনুরূপ কোণ তৈরি করল, 75° এবং 85°
75° ≠ 85°
∴ অনুরূপ কোণ দুটি সমান নয়।

সুতরাং, AB ও CD সমান্তরাল নয়।

6. চিত্রে AB||CD এবং ∠EGB=50°; ∠AGE, ∠AGH, ∠BGH, ∠GHC, ∠GHD, ∠CHFএবং ∠DHF –এর পরিমাপ লিখি।

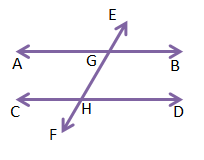
উত্তরঃ-

∠EGB = 50°
∴ ∠AGE = 180° – 50° = 130°
∠AGH = ∠EGB = 50° [বিপ্রতীপ কোণ]
∠BGH = ∠AGE = 130° [বিপ্রতীপ কোণ]
∠GHC = ∠AGE = 130 ° [ কারন, AB || CD, ∴ অনুরূপ কোণ GHC ও AGE পরস্পর সমান ]
∠GHD = ∠AGH = 50° [কারন, AB || CD,, ∴ একান্তর কোণ দুটি পরস্পর সমান ]
∠CHF = ∠AGH = 50° [অনুরূপ কোণ]
∠DHF = ∠BGH = 130° [অনুরূপ কোণ]

7. চিত্রে AB || CD; ∠PQR –এর পরিমাপ লিখি।

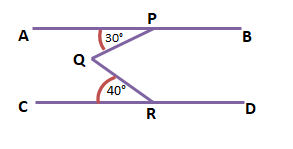
উত্তরঃ-

প্রদত্ত – AB || CD, ∠APQ = 30°, ∠QRC = 40°
অঙ্কন – Q বিন্দু দিয়ে AB ও CD-এর সমান্তরাল করে QS সরলরেখা অঙ্কন করা হল।

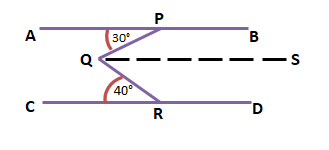
এখন, ∠PQS = ∠APQ = 30° [একান্তর কোণ]
আবার, ∠RQS = ∠QRC = 40° [একান্তর কোণ]
∠PQR = ∠PQS + ∠RQS = 30° + 40° = 70°

8. চিত্রে PQ|| RS, ∠BPQ = 40°, ∠BPR = 155° এবং ∠CRS = 70°; ∆APR-এর কোণগুলির পরিমাপ লিখি।

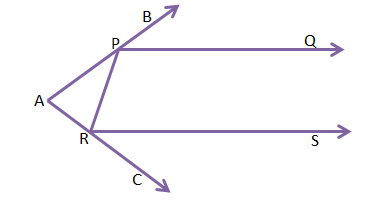
উত্তরঃ-

∠APR = 180° – ∠BPR = 180° – 155° = 25°
∠PRS = 180° – ∠QPR
= 180° – (∠BPR – ∠BPQ)
= 180° – (150° – 40°)
= 180° – 115°
= 65°
∠ARP = 180° – (∠PRS + ∠CRS)
=180° – (65° + 70°) = 180° – 135° = 45°
∆APR-এর ∠A = 180° – (∠APR + ∠ARP) = 180° – (25° + 45°) = 180° – 70° = 110°
∴ নির্ণেয়কোণ গুলি 110°, 45° এবং 25°।

9. AB এবং CD দুটি সমান্তরাল সরলরেখার ভিতর O যেকোনো একটি বিন্দু। OP ও OQ যথাক্রমে AB ও CD সরলরেখার উপর লম্ব। প্রমাণ করি যে P, 0, Q বিন্দু তিনটি সমরেখ।

উত্তরঃ-

AB ও CD দুটি সমান্তরাল সরলরেখা।  O, AB ও CD-এর ভিতর যে-কোনও একটি বিন্দু।  OP ও OQ যথাক্রমে AB ও CD সরলরেখার উপর লম্ব।
প্রমান করতে হবে যে, P, O, Q বিন্দু তিনটি সমরেখ।
অঙ্কন-
O বিন্দু দিয়ে AB ও CD-এর সমান্তরাল করে XY সরলরেখা অঙ্কন করা হল।

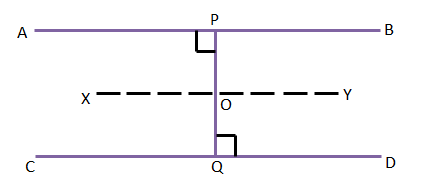
প্রমান-
AB || XY [ অঙ্কনানুসারে ] এবং OP তাদের ছেদক O ও P বিন্দুতে ছেন করেছে।
∴ ∠APO + ∠XOP = 180°
বা, 90° + ∠XOP = 180° [ OP⊥AB প্রদত্ত ]
বা, ∠XOP = 180° – 90° = 90°
আবার, XY || CD [ অঙ্কনানুসারে ] এবং OQ তাদের ছেদক O ও Q বিন্দুতে ছেদ করেছে।
∴ ∠XOQ + ∠OQC = 180° [ প্রদত্ত, OQ⊥CD]
বা, ∠XOQ + 90° = 180°
বা, ∠XOQ = 180° – 90° = 90°
এখন, ∠XOP + ∠XOQ = 90° + 90° = 180°
∠POQ = 180°
সুতরাং, P, O, Q বিন্দু তিনটি সমরেখ।

10. দুটি কোণের প্রতিজোড়া বাহু পরস্পর সমান্তরাল। প্রমাণ করি যে, কোণদুটি সমান অথবা পরস্পর সম্পূরক।

উত্তরঃ-

∠BAC এবং ∠BDC দুটি কোণ। ∠BAC-এর AB ও AC বাহু যথাক্রমে ∠BDC-এর CD ও BD-এর সাথে সমান্তরাল।
প্রমান করতে হবে যে,
∠BAC + ∠BDC = 180° অথবা, ∠BAC = ∠BDC = 90°

প্রমাণ-
AB || CD এবং AC ছেদক, ∴ ∠A + ∠C = 180°
AB || CD এবং BD ছেদক, ∴ ∠B + ∠D = 180°
AC || BD এবং AB ছেদক, ∴ ∠A + ∠B = 180°
AC || BD এবং CD ছেদক, ∴ ∠C + ∠D = 180°
সুতরাং, ∠B + ∠D = ∠A + ∠B
বা, ∠D = ∠A
∴ ∠BAC = ∠BDC
আবার, ∠BAC + ∠BDC = 180°
বা, ∠BAC + ∠BAC = 180°
বা, 2∠BAC = 180°
বা, ∠BAC = 90°
∴ ∠BAC = 90° = ∠BAC ( প্রমানিত)।

11. ABCD সামান্তরিকের AC কর্ণ ∠BAD-কে সমদ্বিখণ্ডিত করে। প্রমাণ করি যে AC কর্ণ ∠BCD -কেও সমদ্বিখণ্ডিত করে।

উত্তরঃ-

ABCD একটি সামন্তরিক।  AC কর্ণ  ∠BAD-কে সমদ্বিখন্ডিত করেছে।
প্রমাণ করতে হবে যে, AC কর্ণ  ∠BCD কেও সমদ্বিখন্ডিত করেছে, অর্থাৎ ∠BCA = ∠ACD

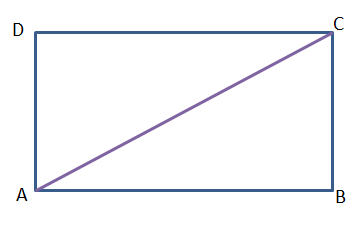
প্রমাণ-
ABCD একটি সামন্তরিক
AB || CD এবং AD || BC
∴ ∠DCA = ∠CAB এবং ∠BCA = ∠CAD [ একান্তর কোণ ]
∠CAD = ∠CAB [ প্রদত্ত, AC, ∠BAD এর সমদ্বিখন্ডক ]
বা, ∠BCA = ∠DCA
∴ ∠BCA = ∠ACD (প্রমানিত)

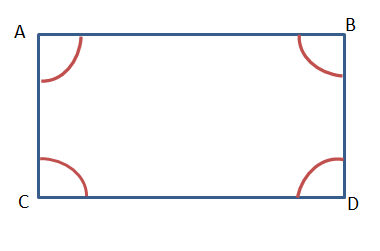
12. প্রমাণ করি যে, সামান্তরিকের একটি কোণ সমকোণ হলে, প্রতিটি কোণই সমকোণ।

উত্তরঃ-

ABCD একটি সামন্তরিক। ∠B = 90°
প্রমাণ করতে হবে যে, ∠A = ∠B = ∠C = ∠D = 90°

প্রমাণ-
ABCD একটি সামন্তরিক।
∴ AB || CD এবং AB তাদের ছেদক A ও B বিন্দুতে ছেদ করেছে।
∴ ∠A + ∠B = 180°
বা, ∠A + 90° = 90°
বা, ∠A = 180° – 90° = 90°
AD || BC এবং AD তাদের ছেদক A ও D বিন্দুতে ছেদ করেছে।
∴ ∠A + ∠D = 180°
বা, 90° + ∠D = 180°
বা, ∠D = 180° – 90° = 90°
আবার, AB || DC এবং BC তাদের ছেদক B ও C বিন্দুতে ছেদ করেছে।
∴ ∠B + ∠C = 180°
বা, 90° + ∠C = 180°
বা, ∠C = 180° – 90° = 90°
সুতরাং, ∠A = ∠B = ∠C = ∠D = 90° (প্রমানিত)

;